
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdfили более спин-орбиталями, поскольку тогда ненулевых миноров M (ij | kl) не существует.
Литература
1.М. Д. Долгушин, Ю. А. Кругляк. Метод разложения в теории ССП и проблема выбора базисных функций в атомных и молекулярных расчетах,
Препринт ИТФ АН УССР, № 57, 1974: https://www.researchgate.net/publication/216156868_Metod_razlozenia_v_teorii_SSP_i_pr oblema_vybora_bazisnyh_funkcij_v_atomnyh_i_molekularnyh_rascetah.
2.М. Д. Долгушин, Ю. А. Кругляк. Расчет атомов методом разложения и выбор гауссовых базисных функций. Конфигурации 1s2 2s2 2 pn ,
Препринт ИТФ АН УССР, № 58, 1974: https://www.researchgate.net/publication/216156866_Rascet_atomov_metodom_razlozenia _i_vybor_gaussovyh_bazisnyh_funkcij_Konfiguracii_1s22s22pn.
3.М. Д. Долгушин, Ю. А. Кругляк. Расчет электронной структуры молекул в базисе гауссовых функций, Препринт ИТФ АН УССР, № 59, 1974: https://www.researchgate.net/publication/216156841_Rascet_elektronnoj_struktury_moleku l_v_bazise_gaussovyh_funkcij.
4.М. Д. Долгушин. Эвристические методы квантовой химии или о смысле научных занятий. Москва: Эдиториал УРСС, 2001.
5.M. Luisier, A. Schenk, W. Fichtner. Full-Band Atomistic Study of Source-to-Drain Tunneling in Si Nanowire Transistors.
In Simulation of Semiconductor Processes and Devices, Eds. T. Grasser and S. Selberherr. Berlin: Springer, 2007.
6.V. V. Zhirnov, R. K. Cavin, J. A. Hutchby, G.I. Bourianoff. Limits to Binary Logic Switch Scaling – A Gedanken Model, Proc. IEEE, v. 91: 11, 1934 (2003).
7.R. Landauer. Irreversibility and heat generation in the computing process, IBM J. Res. Dev., v. 5, 183 – 191 (1961).
8.C. H. Bennett. Notes on Landauer's principle. Reversible Computation and Maxwell's Demon, History Phil. Mod. Phys., v. 34, 501 – 510 (2003).
9.Ю. А. Кругляк. Наноэлектроника “cнизу – вверх”. Одесса: ТЭС, 2015.
10.A. Bérut, A. Arakelyan, A. Petrosyan, S. Ciliberto, R. Dillenschneider, E. Lutz. Experimental verification of Landauer’s principle linking information and thermodynamics, Nature, v. 483, 187 – 189 (2012).
11.К. А. Валиев. Квантовые компьютеры и квантовые вычисления, УФН, т. 175: 1, 3 – 39 (2005).
12.S. Kais. Introduction to quantum information and computation for chemistry, Adv. Chem. Phys., v. 154, 1 – 38 (2014).
13.B. P. Lanyon, J. D. Whitfield, G. G. Gillet et al. Towards quantum chemistry on a quantum computer, Nature chemistry, v. 2, 106 – 111 (2010).
14.J. D. Whitfield, J. Biamonte, A. Aspuru-Guzik. Simulation of electronic structure Hamiltonians using quantum computers, Mol. Phys., v. 109, 735 – 750 (2011).
15.N. C. Jones, J. D. Whitfield, L. Peter at al. Simulating chemistry efficiently on fault-tolerant quantum computers, New Journal Phys., v. 14, 115023 (2012).
16.И. В. Абаренков, В. Ф. Братцев, А. В. Тулуб. Начала квантовой химии.
Москва: Высшая школа, 1989.
17.Н. Ф. Степанов. Квантовая механика и квантовая химия. Москва: МГУ, 2001.
18.Istvan Mayer. Simple theorems, proofs, and derivations in quantum chemistry. New York: Kluwer Academic, 2003.
19.В. В. Иванов, Л. А. Слета. Квантовая химия. Харьков: Фолио, 2007.
50
20.В. И. Барановский. Квантовая механика и квантовая химия. Москва: Academia, 2008.
21.M. Born, J. R. Oppenheimer. Zur Quantentheorie der Molekeln, Ann. Phys., v. 84: 20, 457 – 484 (1927).
22.J. O. Hirschfelder, W. J. Meath. The Nature of Intermolecular Forces, In Advances in Chemical Physics, eds. I. Prigogine, S. Rice, v. 12. New York: John Wiley & Sons, 1967.
23.Р. МакВини, С. Сатклиф. Квантовая механика молекул. Москва: Мир, 1973.
24.R. Pauncz. Spin Eigenfunctions. New York: Plenum Press, 1979.
25.J. C. Slater. The Theory of Complex Spectra, Phys. Rev., v. 34, 1293 – 1323 (1929).
26.P.-O. Lowdin. On the Non-Orthogonality problem Connected with the Use of Atomic Wave Functions in the Theory of Molecules and Crystals, J. Chem. Phys., v. 18, 365 – 375 (1950).
27.J. C. Slater. Molecular energy levels and valence bonds, Phys. Rev., v. 38, 1109 (1931).
28.P.-O. Lowdin. Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction, Phys. Rev., v. 97, 1474 – 1489 (1955).
51
52
Глава 2. Методы решения молекулярного уравнения Шредингера Введение
Точное решение уравнения Шредингера получено лишь для небольшого числа задач, в основном модельных. При расчете конкретных молекулярных систем используются различные приближенные методы. Мы рассмотрим такие приближенные методы решения молекулярного уравнения Шредингера, которые позволяют придать многоэлектронной волновой функции наглядную одночастичную интерпретацию и вместе с тем позволяют учесть значительную часть электронного взаимодействия. Эти методы составляют содержание теории самосогласованного поля (ССП), основы которой были заложены в работах Хартри и Фока [1 – 3]. Рассмотрению некоторых важных результатов, полученных в этом направлении, посвящена эта глава.
Начнем мы с обобщенного метода самосогласованного поля, развитого Годдардом. Дадим свойства решений разных вариантов обобщенного метода ССП и приведем примеры применений. Далее мы рассмотрим метод Хартри – Фока, неограниченные по спину уравнения ХФ, ограниченный метод ХФ и его развитие, метод Хартри – Фока – Рутана.
2.1. Обобщенный метод самосогласованного поля Годдарда и его варианты
Волновая функция системы взаимодействующих электронов в общем случае должна обладать следующими свойствами симметрии. Прежде всего, чтобы теория согласовывалась с экспериментальными данными, волновая функция должна быть антисимметричной относительно перестановки любой пары электронов. В отсутствии зависимости молекулярного гамильтониана от спиновых переменных многоэлектронная волновая функция должна быть собственной функцией оператора квадрата полного спина системы Sˆ2 и оператора проекции полного спина Sˆz на выделенную ось z.
Один из способов построения многоэлектронных волновых функций, обладающих требуемой симметрией, сводится к применению математического аппарата теории групп перестановок [4 – 6]. Неприводимые представления группы перестановок N символов SN классифицируются по схемам Юнга: каждая схема Юнга из N клеток однозначно соответствует определенному неприводимому представлению симметрической группы SN. Поэтому неприводимые представления принято нумеровать символом
соответствующих им схем Юнга [4], где λi – длина i-ой строки схемы Юнга, причем λi+1 ≤ λi . Размерность неприводимого представления [λ] определяется
53

числом стандартных таблиц Юнга, возможных для данной схемы Юнга [λ], и равна [4, 6]
|
N !∏(hi −hj ) |
|
|
||||
f [λ] = |
|
i< j |
|
|
, |
(1) |
|
h |
!h |
!h |
!...h |
! |
|||
|
1 |
2 |
3 |
m |
|
|
|
где hi = λi + m −i , а m есть число строк в схеме Юнга [λ]. Представим волновую функцию N электронов в виде
ˆ |
|
(2) |
Ψ = GΦX , |
|
|
где Φ – некоторая функция пространственных координат N электронов, |
X – |
|
ˆ |
– оператор, выбираемый таким |
|
функция спиновых координат электронов, G |
||
образом, чтобы функция Ψ обладала необходимыми свойствами симметрии. В
ˆ |
можно выбрать в виде [7 – 13] |
|
||||
частности, оператор G |
|
|||||
|
ˆ ˆ µ |
ˆ µ |
µ |
|
|
|
|
G ≡ Gi = ∑ξσˆriOri |
ωˆr |
i |
, |
(3) |
|
|
r |
|
|
|
|
|
где индекс µ задает неприводимое |
представление группы |
SN, индекс i |
||||
соответствует i-ой стандартной таблице Юнга для схемы Юнга µ , ξσˆri есть
четность перестановки σˆri , а |
|
операторы Юнга |
ˆ µ |
и |
µ |
|
определяются |
||||||
|
Ori |
ωˆr |
i |
||||||||||
соотношениями [4 – 6]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ µ |
|
|
f µ |
µ |
|
|
|
|
|
|
|||
Ors |
= |
|
|
|
|
Ur s (τˆ)τˆ, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
N ! ∑τˆ |
|
|
|
|
(4) |
||||
ωˆ µ |
|
|
|
f µ |
|
|
U µ |
(τˆ)τˆ, |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
r s |
|
|
|
|
|
r s |
|
|
|
|
|
||
|
|
|
|
N ! ∑τˆ |
|
|
|
|
|
||||
где Urµs (τˆ) – матричные элементы |
матриц стандартного |
ортогонального |
|||||||||||
представления Юнга – Яманути, а суммированные в (4) производится по всем
N! перестановкам группы SN, индексом |
µ |
обозначено |
неприводимое |
|
представление, сопряженное к µ , операторы |
ˆ µ |
действуют на |
||
Ori |
||||
пространственные координаты электронов, а |
ωˆriµ |
– на спиновые. Поскольку |
||
спиновые координаты электронов принимают лишь два значения, то схема
Юнга |
µ |
может содержать не более двух строк, а схема |
µ – не более двух |
|||||||
столбцов: |
µ = [2m ,1n−m ], |
µ |
= [n,m] , причем |
|
n ≥ m, n + m = N . |
Размерность |
этого |
|||
представления согласно (1) равна: |
|
N !(2S +1) |
|
|
|
|||||
|
|
f [2m ,1n−m ] = f [n,m] ≡ f = |
|
|
|
, |
(5) |
|||
|
|
|
N |
+ S +1 ! N |
− S ! |
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
2 |
|
|
|
|
54
где 2S = n − m .
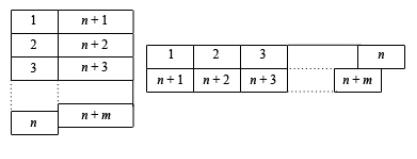
На рис. 1 приведены две сопряженные стандартные таблицы Юнга S[2f m ,1n−m ]
и S1[n,m] .
Рис. 1. Стандартные таблицы Юнга S[2f m ,1n−m ] (слева) и S1[n,m] (справа).
Стандартные таблицы нумеруются в порядке отклонения последовательности чисел в клетках схемы Юнга от натурального ряда, если читать по строкам сверху вниз.
Рассмотрим структуру операторов |
Off |
и ωˆ11 |
, которые понадобятся |
|
ˆ[2m ,1n−m ] |
[n,m] |
|
нам в дальнейшем. Пусть τˆa – некоторая перестановка первых n символов (поднабор a), τˆb – некоторая перестановка последних m символов (поднабор b). Далее, пусть τˆr есть произведение r разных транспозиций, каждая из которых переставляет один символ из поднабора a с одним из символов поднабора b. Любую перестановку группы SN для некоторых τˆa ,τˆb ,τˆr можно представить в виде
τˆ =τˆaτˆbτˆr . |
(6) |
Соответствующие матричные элементы имеют вид [7]
U[2 |
m n−m |
](τˆ τˆ |
τˆ |
|
) =ξ ξ |
|
n −1 |
||||
,1 |
|
|
|
, |
|||||||
ff |
|
a |
|
b r |
τˆa τˆb |
r |
|
||||
U[n, m](τˆ τˆ |
τˆ |
) = (−1)r n −1 , |
|||||||||
|
11 |
a |
b |
r |
|
|
|
r |
|
||
|
|
|
|
|
|
|
|
|
|
||
где биномиальные коэффициенты n |
|
|
≡ |
|
n! |
|
. |
|
|
||
|
(n − r)!r! |
|
|
||||||||
|
|
r |
|
|
|
|
|
|
|||
(7)
(8)
Как показано Годдардом [7], функция GˆiµΦX удовлетворяет принципу Паули
τˆGˆiµΦX=ξτˆGˆiµΦX
и является собственной функцией оператора Sˆ2 , а именно:
Sˆ2GˆiµΦX=S(S +1)GˆiµΦX .
55

Отсюда следует, что выбор |
схемы Юнга определяется |
значением |
|
полного спина S. Выбор i =1,2,3,..., f для построения функции |
|
||
Ψ |
(GI ) |
ˆ µ |
(9) |
|
= Gi ΦX |
||
до некоторой степени произволен; позже мы рассмотрим влияние этого выбора на результаты вычислений.
Отметим также, что операторы Gˆiµ удовлетворяют соотношению [7]
|
1 |
|
ˆ µ |
|
ˆ [1N ] |
|
1 |
|
ˆ |
|
|
∑ |
|
|
∑Gi |
= Ω11 |
≡ |
|
|
∑ξτˆτˆ , |
(10) |
||
f |
µ |
|
|
||||||||
µ |
|
|
i |
|
|
|
N ! τˆ |
|
|||
где антисимметризатор |
Ω11 |
|
есть |
оператор |
Юнга, |
соответствующий схеме |
|||||
|
ˆ [1N ] |
|
|
|
|
|
|
|
|
||
Юнга из одного столбца. |
|
|
|
|
|
|
|
|
|
|
|
Молекулярный гамильтониан |
ˆ |
(6/гл.1) не |
зависит от спинов и |
||||||||
H |
|||||||||||
коммутирует со всеми перестановками координат электронов. Тогда значение энергии [8]
ˆ µ |
ΦX |
|
ˆ |
|
ˆ µ |
ΦX / Ψ |
(GI ) |
| Ψ |
(GI ) |
= Φ |
|
ˆ |
|
ˆ µ |
ˆ µ |
Φ . (11) |
|
|
|
||||||||||||||
|
|
|
||||||||||||||
E = Gi |
|
H |
|
Gi |
|
|
|
H |
|
Oii |
Φ / Φ |Oii |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В дальнейшем нас будет интересовать такая аппроксимация функций вида (9), когда функции Φ и X можно записать следующим образом:
Φ =ϕ1(r1)ϕ2 |
(r2 ) ϕN |
(rN ), |
(12) |
||
X = χ1(s1)χ2(s2 ) χN (sN ), |
|||||
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
χi (si ) |
α(si ), |
|
|
||
= |
β(s ). |
|
|
||
|
|
|
|
||
|
|
i |
|
|
|
Подставляя (12) в (11) и варьируя функционал
I = E −∑ε j 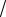 ϕj |ϕj
ϕj |ϕj 
j
по ϕj , получим уравнение для нормированных орбиталей, минимизирующих (11), а именно [8]:
|
|
|
ˆ |
|
|
|
(13) |
|
|
|
Hk (r)ϕk (r) =εk ϕk (r), (k =1,2,3,..., N ) |
||||
где |
ˆ |
|
– довольно |
сложный |
эффективный гамильтониан, |
зависящий от |
|
Hk (r ) |
|||||||
функций ϕk . Уравнения (13) представляют собой набор нелинейных интегродифференциальных уравнений ССП на вариационной функции (2). Иначе говоря, орбитали ϕk (r ) можно рассматривать как функции, описывающие
56

состояние электрона в поле ядер и некотором усредненном поле остальных N − 1 электронов.
Легко установить связь между функцией (9) и вариационной функцией Фока [3] в виде детерминанта Слэтера [14, 15]. Для этого выберем Φ и X в виде
Φ0 |
=τˆ1iϕ1(r1)ϕ1(r2 ) ϕm (r2m−1)ϕm (r2m )ϕm+1(r2m+1) ϕn (rN ), |
(14) |
|||
X0 |
=τˆfiα(1)β(2) |
α(2m −1)β(2m)α(2m +1) |
α(n + m), |
||
|
|||||
где τˆji – перестановка, при помощи которой из таблицы j получается таблица i. Функция GˆiµΦ0X0 совпадает с точностью до фазового множителя со
слэтеровским детерминантом. Таким образом, уравнения (13) являются обобщением уравнений Хартри – Фока, поскольку при переходе от (12) к (14) мы налагаем дополнительные ограничения на вид вариационной функции. Из этого следует, что
|
ˆ µ |
ΦX |
|
ˆ |
|
ˆ µ |
ΦX |
|
Ψ |
(HF ) |
|
|
ˆ |
|
Ψ |
(HF ) |
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||||
E(GI ) = |
Gi |
|
H |
|
Gi |
≤ |
|
|
|
H |
|
. |
(15) |
|||||||
ˆ |
µ |
|
|
ˆ µ |
|
Ψ |
(HF ) |
| |
Ψ |
(HF ) |
||||||||||
|
Gi ΦX |Gi ΦX |
|
|
|
|
|
|
|
|
|||||||||||
При решении уравнений (67) удобно использовать метод Рутана [16]. |
||||||||||||||||||||
Разложим орбитали ϕk по некоторому базису χν : |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ϕk = ∑Cνk χν . (M ≥ N ) |
|
|
|
|
|
|
|
|
|
(16) |
|||||||||
|
|
ν =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда из (13) получим уравнения для коэффициентов разложения |
Cνk вида |
|||||||||||||||||||
|
|
M |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∑Hµν(k )Cνk |
= ∑εk SµνCνk |
, |
|
|
|
|
|
|
(17) |
||||||||||
|
ν =1 |
|
|
ν =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Sµν =  µ ν
µ ν  – интегралы перекрывания базисных функций. Уравнения (17)
– интегралы перекрывания базисных функций. Уравнения (17)
решаются методом последовательных приближений [16]. Следует отметить, что в общем случае (для произвольного i в формуле (9)) матрицы Hµν(k ) зависят от k
[8], что значительно усложняет решение уравнений (17) по сравнению с аналогичными уравнениями на вариационной функции Фока. Однако, если
i = f, т.е. речь идет о вариационной функции Gf ΦX , уравнения (17) принимают |
||
|
ˆ µ |
|
вид [9] |
|
|
M |
M |
|
∑Hµν(a)Cν(ak ) = ∑εk(a)SµνCν(ak ) , |
(18) |
|
ν =1 |
ν =1 |
|
M |
M |
|
∑Hµν(b)Cν(bk) = ∑εk(b)SµνCν(bk) . |
(19) |
|
ν =1 |
ν =1 |
|
57

Таким образом, если использовать оператор для построения волновой
функции (9), то получаем всего два набора уравнений для коэффициентов разложения Cνk . Решив систему уравнений (18) – (19), получим два
ортонормированных набора векторов {Cν(ka) } и {Cν(kb) }. Если же i ≠ f , то в общем случае векторы Cνk не будут ортогональными. Исходя из сказанного, волновую функцию метода GF представим в виде
|
|
Ψ |
(GF ) |
ˆ µ |
, |
(20) |
||||
|
|
|
|
|
= Gf Φ1X1 |
|||||
где |
|
|
|
|
|
|
|
|
|
|
Φ1 =ϕ1a (1) ϕna (n)ϕ1b(n +1) ϕmb(N ) , |
(21) |
|||||||||
X1 =α(1) α(n)β(n +1) β(n +m) , |
(22) |
|||||||||
ϕia = ∑Cν(ia)χν , |
ϕib = ∑Cν(ib)χν . |
(23) |
||||||||
|
ν |
|
|
|
|
|
ν |
|
|
|
Векторы различных поднаборов, вообще говоря, не будут ортогональны, |
||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
ϕia |ϕjb |
|
≠ 0 |
(i, j =1,2,..., M ) . |
(24) |
|||||
Амос и Холл показали [17], что всегда можно сделать такое унитарное |
||||||||||
преобразование функций, входящих в (21), а именно: |
|
|||||||||
|
|
|
n |
|
|
|
ˆ ˆ+ |
ˆ |
|
|
|
ϕ′ |
= |
∑ |
ϕ V |
(25) |
|||||
|
(VV |
= I), |
||||||||
|
ia |
|
|
la li |
|
|
|
|||
|
|
|
l=1 |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
ˆ ˆ + |
ˆ |
|
|
|
ϕ′jb |
= ∑ϕlbUlj |
(26) |
|||||||
|
(UU |
= I), |
||||||||
|
|
|
l=1 |
|
|
|
|
|
|
|
что |
|
|
|
|
|
|
|
|
|
|
ϕ′ |
|ϕ′ |
= λδ |
, |
λ ≤1 i =1,2,...,n . |
(27) |
|||||
ia |
jb |
|
i |
ij |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
j =1,2,...,m |
|
|
Способ получения матриц |
ˆ |
|
ˆ |
в явном виде описан в работах [17, 18]. |
||||||
V |
и U |
|||||||||
Функции, удовлетворяющие уравнениям (27), принято называть
соответствующими орбиталями [19].
Годдард [9] показал, что функция (20) и матрицы операторов Hˆ (a) и Hˆ (b) ,
входящих в уравнения (18) и ( 19), инвариантны относительно преобразования (25), (26). Однако если потребовать, чтобы самосогласованные решения уравнений (18) и ( 19) удовлетворяли (27), то будет потеряна одночастичная интерпретация решения. Иначе говоря, орбитали ϕia′ и ϕib′ нельзя
интерпретировать как состояния электрона в поле ядер и усредненном поле
58
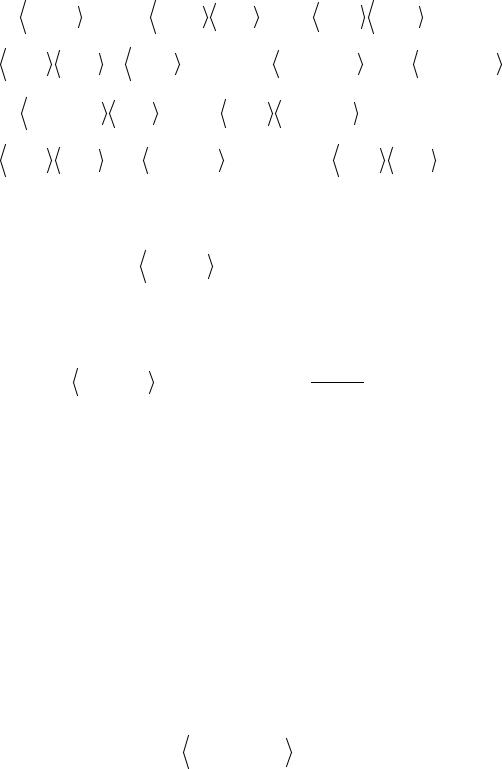
остальных электронов. Более того, матрицы операторов Hˆ (a) и зависеть от k. С другой стороны, вычислять матрицы операторов энергию гораздо проще на орбиталях ϕia′ и ϕib′ , чем на орбиталях ϕia
Матрица оператора Hˆ (a) имеет вид [9]
Hˆ (b) , Hˆ (a) ,
и ϕib .
будут
Hˆ (b) и
(a) |
ˆ |
a |
|
|
ˆ |
|
a,vb |
ˆ |
a,i |
|
Hµν |
≡ µ |h |ν a |
+∑ |
µ |h |i vb |ν i, a + µ |νb |
i |h |
|ν vb, a |
|
||||
|
|
|
|
i,v |
|
|
|
|
|
|
+∑ µ |ub vb |ν |
|
ˆ |
a, vb,i |
|
a,i |
+ µ,i | gˆ |
a,i |
|||
∑ i |h |
| j ub, a, j +∑ |
µ,i | gˆ |ν, j |
a, j |
| j,ν j, a |
||||||
u,v |
|
|
i, |
j |
|
i, j |
|
|
|
|
+ ∑ |
|
| j,t |
|
|
a,vb,i |
|
|
a, j,t |
|
|
µ,i | gˆ |
|
vb |ν j, a,t |
+ µ |νb j,t | gˆ |ν,i vb, a,i |
|
||||||
i, j, t;v |
|
|
|
|
|
|
|
|
|
|
+∑ µ |ub vb |ν |
∑ i, j | gˆ | s,t uba, vb, a,,is,,jt − E∑ µ |ub vb |ν uba,vb, a |
|||||||||
u,v |
|
|
i< j; s, t |
|
|
u,v |
|
|
|
|
и аналогично для H |
|
, где |
|
|
|
|
|
|
||
|
|
ˆ (b) |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
* |
ˆ |
|
|
|
|
µ | A|vb ≡ ∫dr χµ (r)A(r)ϕvb(r) , |
|||||||||||
|
ˆ |
|
|
|
1 |
ˆ |
|
|
|
|
|
|
h(r) |
= − 2 |
∆ +V |
(r) , |
|
|
|||||
i, j | gˆ |t,s ≡ ∫dr1 dr2 |
ϕi*(r1)ϕt (r1) |
|
1 |
| |
ϕ*j (r2 )ϕs (r2 ) . |
||||||
|
|
|
|
|
|
|
|
| r1 |
−r2 |
|
|
Величины есть сложные |
|
функции |
интегралов перекрывания |
||||||||
определенных в (27), например: |
|
|
|
|
|
|
|
|
|
|
|
|
m−1 |
n |
|
−1 |
|
|
|
|
|
|
|
aa |
Ap ≡T 00, |
|
|
||||||||
= ∑ |
|
|
|||||||||
|
p=0 |
p |
|
|
|
|
|
|
|
||
Ap = |
∑ |
|
xk1 xk2 xkp , |
xk |
= λk2 . |
||||||
{k1,k2 ,...,kp} |
|
|
|
|
|
|
|
|
|||
|
(ki ≠k j ) |
|
|
|
|
|
|
|
|
|
|
(28)
λi ,
Из (28) следует, что всего имеется 78 матриц операторов ˆ . Выражения для всех матриц, приведенных в [9] для Hˆ (a) и Hˆ (b) , построены на орбиталях, удовлетворяющих (27). Интеграл нормировки для функции (20)
Ψ(GF ) | Ψ(GF ) =T 00 . |
(29) |
59
