Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991

Электронное уравнение (5) имеет множество решений Ψe (r; R) , каждое из которых определяет ППЭ E(R) для основного и возбужденных состояний, каждая из которых может быть далее использована как потенциальная энергия для изучения движения ядер.

Ядерное уравнение имеет вид

в котором ядерный гамильтониан

а волновая функция ΨN (R) зависит только от ядерных координат.

Покажем почему выражение (4) не может быть точным равенством. Подставим (4) в полное уравнение Шредингера (1), а именно:

При исследовании этого уравнения проблемы вызывает кинетическая энергия ядер

в записи которой, как и везде далее, опущены значения индекса суммирования, поскольку они очевидны, а оператор Лапласа

При раскрытии уравнения (9) встретятся вторые производные по декартовым координатам ядер. Например, производная по Xα-координатам имеет вид:

30

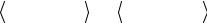
где первые два слагаемых в квадратных скобках содержат производные электронной волновой функции по координатам ядер, а второе и третье слагаемые содержат производные ядерной волновой функции по координатам ядер. Подобные производные не входят ни в электронное уравнение (5), ни в ядерное (7). Это означает, что решая сначала уравнение (5), а потом (7), как мы сейчас увидим, невозможно получить точное решение полного уравнения Шредингера (1). Эти неувязки, возникающие за счет движения ядер, приводят к не всегда пренебрежимо малому зацеплению между различными электронными состояниями, рассчитанными в приближении Борна – Оппенгеймера.

Обозначим сумму всех таких зацепляющихся неувязок

Врутинных расчетах обычно пренебрегают зацепляющимися неувязками (14). В них фигурируют производные электронной волновой функции, деленные на массы ядер, которые намного больше массы электрона. Поэтому неувязки малы. Они обычно намного меньше чем ошибки, которые всегда имеют место при решении самих уравнений, получающихся в приближении Борна – Оппенгеймера, особенно вблизи равновесных конфигураций молекул.

Вслучае проведения расчетов в т. наз. адиабатическом приближении (адиабатические процессы в термодинамике не имеют никакого отношения к этой не совсем удачной, но уже устоявшейся в квантовой химии терминологии) вычисляются средние значения неувязок по рассматриваемому электронному

состоянию Ψe , а именно:

где, удобства ради, используются дираковские обозначения для матричных элементов (см. Приложение П-2), в этом случае диагональных. Эти средние добавляют к ядерному гамильтониану (8). Второе слагаемое в (16) является

31

линейным дифференциальным оператором α , зависящим от {R} и действующим на ядерную волновую функцию ΨN (R) .

Полезно сравнить доступные точные результаты, полученные в разных приближениях для наиболее легкой молекулы – молекулы водорода. В табл. 2 сопоставлены энергии диссоциации H2 , HD и D2 , посчитанные в разных

приближениях с учетом нулевой энергии колебаний.

Таблица 2 Энергии диссоциации молекул H2 , HD и D2 из наинизшего колебательного и

наинизшего вращательного состояний, см−1 [22].

Это сопоставление показывает, что приближение Борна – Оппенгеймера дает блестящие результаты, по-видимому, за счет случайной компенсации ошибок вычислений. Неожиданно худшие результаты, полученные в неадиабатических расчетах связывают с тем, что в расчетах не был достигнут абсолютный минимум. Можно ожидать, что для молекул с более тяжелыми ядрами приближение Борна – Оппенгеймера будет работать еще точнее.

Большинство термических химических реакций протекают адиабатически в том смысле, что система участвующих в реакции атомов остается на ППЭ, отвечающей обычно основному электронному состоянию. Под неадиабатическими реакциями обычно подразумевают реакции с переходом с одной ППЭ на другую. Это имеет место при таких конфигурациях ядер, когда две ППЭ подходят достаточно близко друг к другу. Подробное обсуждение приближения Борна – Оппенгеймера можно найти в [18].

1.2.Волновые функции

1.2.1.Спин-орбитали

Спин-орбиталью принято называть одноэлектронную волновую функцию,

32

Собственный момент импульса электрона, иначе спин, может принимать

в котором первая строка соответствует спину σ = +1/ 2 , а вторая строка – спину

σ = −1 / 2 :

Зависимость от спина выражают с помощью спиновых функций α и β :

На практике обычно используют спин-орбитали, соответствующие чистым одноэлектронным спиновым состояниям со спином «вверх» и «вниз»: ψ(r )α(σ)

и ψ(r ) β(σ) .

Спиновые операторы действуют в двухмерном пространстве спиновых функций α и β и представляются матрицами размера 2 ×2 :

где они записаны в атомных единицах через матрицы Паули:

Заметим, что матрицы Паули в стандартных учебниках квантовой механики вводятся постулативно; вывод выражений для матриц Паули можно найти в [9].

33

Свойства спиновых операторов (22):

б) спиновые операторы как операторы момента импульса подчиняются коммутационным соотношениям:

Поскольку спиновая переменная σ принимает только дискретные значения + 12 и − 12 , при вычислении средних значений матричных элементов

операторов физических величин, зависящих как от спиновых переменных, так и от пространственных переменных, по спиновым переменным нужно просто суммировать:

Использование спин-орбиталей, построенных из чистых спиновых функций α и β , в силу ортонормировки (27) существенно упрощает суммирование по спину, а именно: ненулевое значение получаем только тогда,

34

когда в бра- и кет-скобке для каждого электрона имеем одну и ту же спиновую функцию, и тогда суммирование по спину дает единичный множитель.

где для всех пространственных и спиновых переменных электронов 1 и 2 использовались сокращенные обозначения «1» и «2», а именно:

1.2.2. Многоэлектронные спиновые состояния

Гамильтониан Борна – Оппенгеймера (6) безспиновый и поэтому коммутирует со спиновыми операторами Sˆz и Sˆ2 . Как следствие этого, собственные функции гамильтониана (6) можно классифицировать по

названия: синглет (S = 0) , дублет (S =1/2) , триплет (S =1) , …

Подробно о построении многоэлектронных спиновых функций см. [23, 24].

1.2.3. Детерминанты Слэтера

Электроны являются фермионами. При одновременной перестановке пространственных и спиновых координат любой пары электронов многоэлектронная волновая функция должна менять знак на противоположный, т. е. должна быть антисимметричной по всем парам электронов:

35

Разработаны различные методы антисимметризации многоэлектронной волновой функции, однако, в практических расчетах пространственные и спиновые координаты отдельных электронов удобно описывать совместно в виде детерминанта Слэтера [25], построенного из спин-орбиталей

ψk (i) ≡ψk (ri ,σi ) , в которых оба индекса пробегают независимо друг от друга один

итот же набор значений 1,2,3,..., N , что и обеспечивает антисимметричность, поскольку речь идет об определителе:

Позже при рассмотрении правил Слэтера вычисления матричных элементов операторов мы убедимся в том, что множитель 1/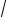N ! обеспечивает нормировку волновой функции (34) на единицу при условии, что волновая функция построена из ортонормированных одноэлектронных спин-орбиталей.

Из свойств определителей следует, что все спин-орбитали, используемые для построения волновой функции, должны быть линейно-независимые, в противном случае Ψ ≡ 0 . К такому же результату приводит появление в определителе одной и той же спин-орбитали дважды, т.е. в любом состоянии может существовать только один электрон (принцип Паули), а каждая пространственная орбиталь может быть занята максимум двумя электронами: один со спином α , второй со спином β .

Волновую функцию (34) компактно записывают через антисимметризатор

действующий на хартриевское произведение спин-орбиталей, а сам оператор антисимметризации Αˆ определяется как

где суммирование ведется по всем перестановкам Pˆ , возможным для N различных чисел . Все эти перестановки образуют симметрическую группу SN . Множитель называют четностью перестановки Pˆ . Основные свойства перестановок приведены в Приложении П-3.

36

Запись волновой функции в виде (35) с антисимметризатором (36) есть просто иной способ записи детерминанта Слэтера (34), поскольку при действии оператора антисимметризации Αˆ на хартриевское произведение

ψ1(1)ψ2 (2)ψ3(3) ψN (N ) получаем

что есть ничто иное как запись определителя (34) в виде суммы по всем перестановкам симметрической группы.

Одно из свойств определителя состоит в том, что строки и столбцы можно менять местами без изменения определителя. Это означает, что правую часть предыдущего выражения можно также записать как действие оператора антисимметризации на индексы спин-орбиталей, а именно:

что доказывается без труда прямой подстановкой.

Оператор антисимметризации Αˆ с точностью до постоянного коэффициента является проекционным оператором, который действуя на какую-либо волновую функцию извлекает из нее составляющую, антисимметричную по перестановкам любых пар электронов. Напомним, что оператор является проекционным тогда и только тогда, когда он является эрмитовым и идемпотентным (Приложение П-2).

Легко показать прямой подстановкой, что

оператор

что и служит доказательством эрмитовости оператора антисимметризации.

37

Оператор антисимметризации Aˆ коммутирует с любым оператором, симметричным относительно координат всех электронов. Такими операторами являются гамильтониан Борна – Оппенгеймера (6), операторы полного спина

и его проекции Sˆz .

Еще одним важным свойством детерминантных волновых функций является следующее. При смешивании занятых спин-орбиталей в детерминантной волновой функции Ψ = Αˆ [ϕ1(1)ϕ2 (2)ϕ3(3) ϕN (N )] , т. е. при

выполнении над детерминантом любого неособенного (имеющего ненулевой определитель) линейного преобразования, которое сводится к замене исходных спин-орбиталей ϕi на спин-орбитали

исходная детерминантная волновая функция изменится лишь на физически несущественный нормировочный множитель, равный определителю линейного преобразования:

определитель любой унитарной матрицы равен по абсолютной величине единице, имеем:

Итак, детерминантная волновая функция инвариантна относительно унитарного преобразования занятых орбиталей с точностью до физически несущественного фазового множителя, по модулю равного единице. Это свойство инвариантности является обобщением известного свойства определителя, согласно которому его значение не изменяется, если к каждому элементу столбца (строки) добавить элементы другого столбца (строки), умноженные на произвольное число.

38

Следствием предыдущего вывода (44) является то обстоятельство, что любую детерминантную волновую функцию всегда можно построить (с точностью до постоянного множителя) из ортонормированных спинорбиталей. Например, симметричной ортогонализации по Лёвдину [26] соответствует использование в (42) матрицы преобразования Τ = S−1/2 , где Sij = ϕi |ϕj есть интегралы перекрывания спин-орбиталей, используемых для

построения детерминанта Ψ . В общем случае ортонормированные орбитали можно получить используя любую матрицу преобразования Τ = S−1/2V , где V – произвольная унитарная матрица.

Итак, детерминантная волновая функция с точностью до физически несущественного постоянного множителя определяется подпространством, растянутым занятыми спин-орбиталями. Детерминантную волновую функцию можно строить из любого набора линейно независимых одноэлектронных функций, лежащих полностью в этом подпространстве.

1.3. Матричные элементы между слэтеровскими детерминантами

Технику вычисления матричных элементов различных операторов между слэтеровскими (детерминантными) волновыми функциями, построеными из ортонормированных спин-орбиталей, предложил Слэтер [25, 27]. Лёвдин рассмотрел более общий случай неортогональных орбиталей [28].

Нам понадобится общая формула Лёвдина для перекрывания детерминантных волновых функций

где мы воспользовались тем, что оператор Hˆ (1) коммутирует с оператором антисимметризации Αˆ , эрмитовостью Hˆ (1) и его идемпотентностью (38), а

39