
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
Александров А.Ф., Кузелев М.В. Физика электронных пучков
σ |
|
= |
(xi2 − xi2−1 )J0 (µ0n xˆi ) |
|
, |
xˆ |
= |
1 |
(x |
+ x − ), |
x = |
r |
. |
(31.14) |
||||
|
|
) |
2 |
|
||||||||||||||
|
in |
|
q |
(x2 |
− x2− |
)J 2 (µ |
xˆ |
|
i |
|
i |
i 1 |
|
R |
|
|||
|
|
|
∑ |
i |
i 1 |
0 |
0n i |
|
|
|
|
|
|
|
|
|
||
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Плотность зарядов в слое i |
вычислим по рассмотренному выше методу крупных час- |
|||||||||||||||||
тиц. Пусть крупная частица представляет собой коаксиальный цилиндр с радиусами ri−1 и ri
и длиной h , а плотность заряда внутри цилиндра пусть совпадает с невозмущенной плотностью заряда пучка. Очевидно, что такой крупной частице соответствует регуляризирующая функция (31.6б). Длину h положим равной ячейке разностной сетки по z , взятой для решения дифференциального уравнения (31.13). Окончательные уравнения для численного интегрирования следуют из (31.2), (31.7) и (31.13) и имеют вид
|
dyij |
|
=ηij , |
|
dηij |
= −(1− β 2ηij2 )3 2 ∑p |
J0 (µ0n xˆi ) |
∂Φn , |
|
|
dτ |
|
dτ |
||||||
|
|
|
n=1 |
|
∂y |
||||
|
∂2Φ |
n = µ2 |
ξΦ |
|
−νW , |
|
(31.15) |
||
|
∂y2 |
|
|
||||||
|
0n |
|
|
n |
n |
|
|
||
|
|
|
q |
∑(∆(| y − yij |) − ∆(| y − y0ij |)). |
|
||||
Wn = ∑σin |
|
||||||||
|
|
|
i=1 |
|
j |
|
|
|
|
Здесь ∆- функция (31.6б), и использованы следующие безразмерные переменные и обозначения:
y = |
z , |
τ = |
|
t |
|
, |
η = v , Φ |
n |
= eϕn |
, |
|
L |
|
L u |
|
u |
mu2 |
(31.16) |
|||
|
L2 |
|
|
ωb2 L2 |
, β 2 = u2 . |
|||||
ξ = |
, ν = |
|
||||||||
|
R2 |
|
|
|
u2 |
c2 |
|
|
|
|
Отметим, что в величине Wn |
|
осуществляются суммирования как по слоям (индекс i ), |
||||||||
так и по крупным частицам каждого слоя (индекс j ). В случае тонкого трубчатого электрон-
ного пучка с дельтаобразным поперечным профилем плотности вида (31.5) (см. также (31.7)), суммирование по слоям отсутствует (есть только один слой) и вместо уравнений (31.15) будут иметь место следующие:
|
dyi |
= |
ηi , |
dηi |
|
= −(1− β 2ηi2 )3 2 ∑p ∂Φn , |
|||||||||
|
|
dτ |
|
||||||||||||
|
dτ |
|
|
|
|
|
|
|
n=1 |
∂y |
|||||
|
∂ |
2Φ |
n |
= µ2 |
ξΦ |
|
|
−νG W , |
|
|
(31.17) |
||||
|
|
∂y2 |
|
|
|
|
|||||||||
|
|
|
0n |
n |
|
|
n |
|
|
|
|||||
W = ∑(∆(| y − yi |) − ∆(| y − y0i |)). |
|||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
Здесь G |
n |
= 2∆ r J 2 (µ |
0n |
r |
R) R2 J 2 |
( µ |
0n |
) . |
|||||||
|
|
|
|
|
b b |
0 |
|
b |
1 |
|
|
||||
Перейдем к обсуждению результатов численного моделирования нелинейной динамики неустойчивости Пирса. При решении уравнений (31.15) учитывалось десять слагаемых
141
Александров А.Ф., Кузелев М.В. Физика электронных пучков
в сумме по n (т.е. обусловленное нелинейным расслоением пучка искажение поперечного распределения потенциала описывалось с точностью ~ 0,1R ), шаг по переменной y состав-
лял 5 10−3 (при этом в невозмущенном пучке на длине резонатора находилось 200 крупных частиц), а третье уравнение системы (т.е. уравнение Пуассона) интегрировалось методом прогонки. В переменных (31.16) решение задачи зависит только от параметров ξ , ν и β .
Ниже приведены результаты расчета для ξ = 25 , β =0,8 и νγ0−3 =13 . Такой выбор параметров обеспечивал заметную неодномерность системы ( L > R ), большое значение линейного инкремента неустойчивости и близость тока пучка к предельному току Пирса (αПирса =1,13).
На Рис. 31.1 изображены для различных моментов времени фазовые плоскости электронов пучка для трех значений поперечной координаты r : по горизонтальной оси отложены безразмерные продольные координаты крупных частиц yi , по вертикальной – их безраз-
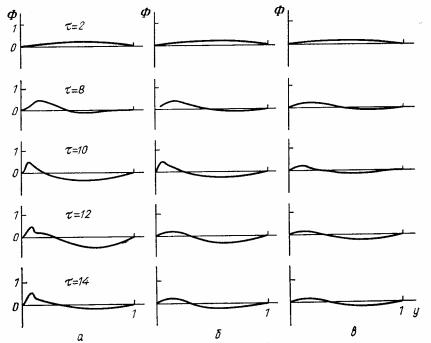
мерные скорости ηi . На Рис. 31.2 для тех же расстояний от оси и тех же моментов времени показано распределение потенциала Φ(τ, x, y) = ∑Φn (τ, y)J0 (µ0n x) . Основные результаты хорошо видны из рисунков, поэтому ограничимся их перечислением.
1.В резонаторе образуется так называемый виртуальный катод – область пространства, от которой электроны пучка отражаются обратно в сторону плоскости инжекции. Развитие виртуального катода является основным нелинейным итогом неустойчивости Пирса, приводящим к сильному искажению транспортируемого тока.
2.Время образования виртуального катода (τ ≈10 ) превышает время пролета электроном пучка резонатора. Данный результат, очевидно, зависит от способа возбуждения неустойчивости. В рассматриваемом случае начальное возмущение представляло собой сгущение плотности электронов (на уровне 5%) в среднем сечении резонатора.
3.Виртуальный катод образуется только вблизи оси резонатора. При удалении от оси возмущение потенциала (т.е. потенциальный барьер тормозящий электроны) падает, а фазовые траектории электронов приближаются к прямым линиям.
4.Виртуальный катод расположен у самого входа в резонатор – на расстоянии, более
чем в два раза меньшем радиуса R . Причем оказалось, что Lк ≈ rDe = γ03 2u ωb , где Lк - рас-
стояние от входа до виртуального катода, а rDe - «дебаевский радиус» электрона пучка. Заме-
тим, что около необходимого порога (29.13) неустойчивости Пирса в рассматриваемой здесь системе дебаевский радиус имеет порядок R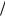 µ01 .
µ01 .
5. В масштабе времен пролета (τ ≈1 ) виртуальный катод меняется мало, т.е. может считаться стационарным. Однако существуют более быстрые изменения его структуры с ха-
142

Александров А.Ф., Кузелев М.В. Физика электронных пучков
Рис. 31.1
Фазовые плоскости электронов при неустойчивости Пирса в резонаторе:
а – на оси резонатора; б – на расстоянии 0,2R от оси; в – на расстоянии 0,6R от оси
143
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Рис. 31.2
Распределение потенциала при неустойчивости Пирса в резонаторе:
а – на оси резонатора; б – на расстоянии 0,2R от оси; в – на расстоянии 0,6R от оси
144
Александров А.Ф., Кузелев М.В. Физика электронных пучков
рактерным временем τ ~ Lк 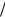 L . Последнее из рисунков не видно, но подтверждается анали-
L . Последнее из рисунков не видно, но подтверждается анали-
зом колебаний числа крупных частиц в области 0,5Lк < y <1,5Lк .
6. Виртуальный катод не приводит к полному запиранию тока через резонатор. Наиболее сильно ток искажается на оси резонатора, где количество отраженных электронов достигает 50% в их общем балансе. На расстоянии 0,2R от оси отраженных электронов практи-
чески нет. Последний вывод справедлив только, если пучок однороден по всему поперечному сечению резонатора. В случае поперечно неоднородных пучков искажение более значительно. Например, ток тонкого трубчатого пучка срывается полностью, что было установлено при численном интегрировании уравнений (31.17).
145
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Глава VII. Неустойчивости прямолинейных электронных пучков в плазме
§ 32. Черенковская пучковая неустойчивость
Рассмотрим пространственно неограниченную холодную электронную плазму, пронизываемую таким же неограниченным моноскоростным электронным пучком малой плотности (α = e - электроны плазмы; α = b - электроны пучка). Направим ось OZ координатной системы вдоль невозмущенной скорости электронного пучка ur = {0,0,u} и рассмотрим в ли-
нейном приближении потенциальные (электростатические) возмущения пучково-плазменной системы, зависящие только от координаты z и времени t . Исходим из следующих линейных уравнений для возмущений плотностей токов плазмы и пучка (см. уравнения (27.2) и (28.5)):
∂j |
|
= |
ω2 |
E |
, |
|
|
|
|
|
|
|
|||
|
|
|
e |
|
Le |
|
|
|
|
|
|
|
|||
∂t |
|
4π |
z |
|
|
|
|
|
|
|
(32.1) |
||||
∂ |
|
|
∂ |
2 |
|
|
ω2 |
γ −3 |
∂E |
|
|||||
+ u |
j |
= |
z . |
|
|||||||||||
|
|
|
|
|
|
Lb |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
∂t |
|
|
∂z |
b |
|
4π ∂t |
|
|
|||||||
Здесь ω |
Lb |
= |
|
4πe2n |
m , |
ω |
Le |
= 4πe2n |
m - ленгмюровские частоты электронов пучка и |
||||||
|
|
|
|
|
|
0b |
|
|
|
|
0e |
|
|||
плазмы, а γ = (1 − u2 |
c2 )−1 2 − невозмущенный релятивистский фактор электрона пучка. При |
||||||||||||||
записи уравнений (32.1) знак “~” у возмущенных величин был опущен. |
|
|||
Для вычисления электрического поля используем уравнение Максвелла |
divE = 4πρ |
|||
для компоненты Ez |
(кроме этой компоненты других составляющих электромагнитного поля |
|||
в рассматриваемой системе и для рассматриваемых возмущений нет) |
|
|||
|
∂Ez |
= 4π(ρe |
+ ρb ), |
(32.2) |
|
∂z |
|||
|
|
|
|
|
в котором |
ρe и ρb |
−возмущения плотностей заряда электронов плазмы и пучка соответст- |
||
венно. Подчеркнем, что в (32.2) входят именно возмущения плотностей заряда, поскольку средний статический заряд нейтрализован неподвижным ионным фоном. Возмущения плот-
ностей зарядов ρe |
и ρb связаны с возмущениями плотностей токов уравнениями непрерыв- |
|||||
ности |
|
|
|
|
||
|
∂ρe,b |
+ |
∂je,b |
= 0 . |
(32.3) |
|
|
|
∂z |
||||
|
∂t |
|
|
|||
Представляя возмущенные величины в виде ~ exp(−iωt +ikz z) , получим из уравнений |
||||||
(32.1) - (32.3) следующее дисперсионное соотношение |
|
|||||
|
ω2 |
|
ω2 γ −3 |
(32.4) |
||
1 − ω2 |
− (ω − kzu)2 = 0, |
|||||
|
Le |
|
|
Lb |
|
|
которое является одним из ключевых уравнений линейной теории неустойчивостей элек146
Александров А.Ф., Кузелев М.В. Физика электронных пучков
тронных пучков в плазме. Левая часть (32.4) есть продольная диэлектрическая проницаемость пучково-плазменной системы. Действительно, первое и третье слагаемые, как следует из (27.5), составляют продольную диэлектрическую проницаемость релятивистского электронного пучка. Тогда, по аналогии, второе слагаемое дает вклад в диэлектрическую проницаемость от электронов холодной плазмы. При анализе дисперсионного уравнения (32.4) будем предполагать, что выполнено неравенство
ωLb2 γ −3 << ωLe2 . |
(32.5) |
Уравнение (32.4) является алгебраическим уравнением четвертого порядка относительно частоты ω . Следовательно, общее решение системы (32.1) - (32.3), например, для плотности тока в плазме имеет вид
4 |
|
je = ∑Cn exp(−iωnt + ikz z), |
(32.6) |
n=1
где Cn − постоянные, определяемые из начальных условий, а ωn = ωn (kz )−корни дисперси-
онного уравнения (32.4). Каждый из этих четырех корней определяет дисперсию одной из нормальных (собственных) волн рассматриваемой пучково-плазменной системы. Алгебраическое уравнение четвертого порядка с действительными коэффициентами имеет или четыре действительных корня, или, по крайней мере, – два комплексно-сопряженных корня. В последнем случае одна из частот ωn имеет положительную мнимую часть. Соответствующее этой частоте слагаемое в (32.6) экспоненциально нарастает со временем, что означает неустойчивость пучково-плазменной системы.
На Рис. 32.1 изображены дисперсионные кривые ωn (kz ) уравнения (32.4). Асимпто-
тами этих кривых являются линии ω = ±ωLe и ω = kzu ±ωLbγ −3 2 . Видно, что в области волно-
2 . Видно, что в области волно-
вых чисел kz между отметками «1» и «2» каждому волновому числу соответствуют только два действительных значения частоты. Следовательно, в этой области волновых чисел два других значения частоты являются комплексными, и имеет место пучковая неустойчивость.
В областях волновых чисел левее отметки «1» и правее отметки «2» каждому kz соответст-
вуют четыре действительных значения частоты, и неустойчивости при таких значениях kz
нет.
Перейдем к решению уравнения (32.4). Поскольку выполнено неравенство (32.5), вклад пучка в дисперсионное уравнение может быть существенным только в той части плос-
кости (ω, kz ), где ω ≈ kzu . Поэтому ищем решение уравнения (32.4) в виде
ω = kzu +δω, |
(32.7) |
где δω −поправка к частоте, удовлетворяющая, в силу условия (32.5), неравенству
147

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ω
ωLe
1 |
2 |
kz |
| |
| |
|
-ωLe
Рис. 32.1
Дисперсионные кривые пучково-плазменной системы.
148
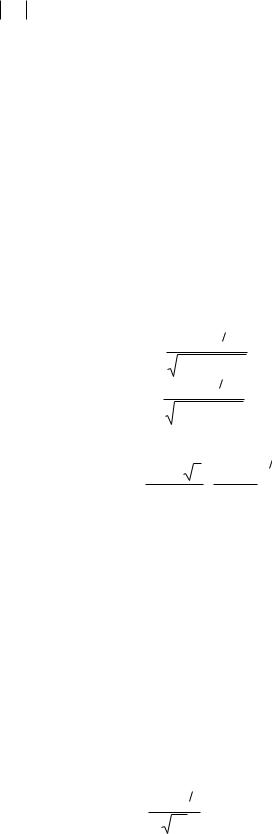
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
δω << | kz | u, ωLe . |
(32.8) |
Конечно, не все решения дисперсионного уравнения (32.4) можно представить в виде (32.7) с поправкой δω , удовлетворяющей неравенству (32.8). Но для интересующих нас комплексных частот, когда одна из поправок δω определяет инкремент пучковой неустойчивости, такое представление при выполнении неравенства (32.5) верно.
Подставляя (32.7) в уравнение (32.4) и учитывая (32.8), преобразуем его к виду
|
|
ω |
2 |
|
|
|
|
ω |
Le |
3 |
δω |
|
ω2 |
γ −3 |
|
|
|
− |
|
Le |
|
+ 2 |
|
|
|
|
− |
Lb |
|
2 = 0. |
(32.9) |
||
2 |
|
|
|
|
|
|||||||||||
1 |
|
2 |
|
|
|
|
|
ωp |
δω |
|||||||
|
|
kz u |
|
|
|
kzu |
|
|
|
|||||||
При kzu ≠ ±ωLe , в силу неравенства (32.8), вторым слагаемым в левой части уравнения (32.9)
можно пренебречь. Наоборот, при kzu = ±ωLe учет второго слагаемого необходим. Соответ-
ственно сказанному имеются два принципиально различных решения уравнения (32.9):
|
|
|
ω |
Lb |
γ −3 2 |
|
|
|
|
||||
|
± i |
|
|
|
|
kzu, |
| kz | u < ωLe , |
|
|||||
|
ωLe2 |
|
− kz2u2 |
|
|||||||||
I. |
|
|
|
|
|
|
(32.10) |
||||||
| kz | u ≠ ωLe : δω = |
|
|
|
|
|
−3 2 |
|
|
|
||||
|
|
± |
ωLbγ |
|
kzu, |
| kz | u > ωLe . |
|
||||||
|
2 |
|
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
kz u |
|
|
−ωLe |
|
|
|
|
|||
|
|
−1 ± i |
3 |
|
|
2 |
−3 |
1 3 |
|
|
|||
II. |
| kz | u = ωLe : δω = |
|
|
ωLbγ |
|
|
ωLe . |
(32.11) |
|||||
|
|
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
2ωLe |
|
|
|
||
Из (32.10), (32.11) следует, что при выполнении (32.5) удовлетворяются и неравенства (32.8). Для выяснения физического смысла решений (32.10) рассмотрим продольные волны электронного пучка в изотропном диэлектрике с постоянной диэлектрической проницаемостью ε0 (например, в нейтральном газе). Дисперсионное уравнение таких волн получается заменой в уравнении (32.4) диэлектрической проницаемости плазмы 1 −ωLe2 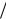 ω2 на проницае-
ω2 на проницае-
мость среды ε0 . А именно:
|
ω2 γ −3 |
= 0. |
|
|
|
(32.12) |
ε0 − (ω − kzu)2 |
|
|
|
|||
|
Lb |
|
|
|
|
|
Из (32.12) определяем спектры двух пучковых волн – быстрой и медленной |
|
|||||
ω = kzu +δω, |
δω = ± |
ω |
|
γ −3 2 |
(32.13) |
|
|
Lb |
. |
||||
|
|
|
|
|
ε0 |
|
Хотя диэлектрическая проницаемость плазмы, в отличие от постоянной величины ε0 , сильно зависит от частоты, поправка δω из формулы (32.13) в принципе не отличается от второй части формулы (32.10). Действительно, возмущения плотности заряда пучка, имеющие про-
странственный период 2π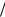 | kz | , движутся вместе с пучком со скоростью u . Такие возмуще-
| kz | , движутся вместе с пучком со скоростью u . Такие возмуще-
149

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ния действуют на плазму с частотой kzu . Отклик плазмы на такое воздействие определяется ее продольной диэлектрической проницаемостью на частоте воздействия, равной
εl |
|
|
ω |
2 |
|
|
ω2 |
(32.14) |
|
|
|
|
|||||||
|
=1 − |
Le2 |
|
=1 − |
Le |
≡ εe , ωLe ≠| kz | u. |
|||
|
|
2 2 |
|||||||
|
|
ω=kzu |
ω |
|
ω=kzu |
|
kz u |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Легко видеть, что вторая часть формулы (32.10), с использованием (32.14), может быть записана в виде, сходном с (32.13),
δω = ± |
ω |
|
γ −3 2 |
(32.15) |
|
Lb |
. |
||
|
|
|
εe |
|
Таким образом, при | kz | u > ωLe |
мы имеем обычные пучковые волны в среде, диэлектриче- |
|||
ская проницаемость которой определяется плазмой.
Но в виде (32.15) записывается и первая часть формулы (32.10), когда | kz | u < ωLe и
диэлектрическая проницаемость плазмы εe отрицательна. В этом случае (32.15) удобно пе-
реписать в виде
δω = ±i |
ω |
Lb |
γ −3 2 |
, |
(32.16) |
|
|
| εe | |
|
|
|
что при | kz | u < ωLe совпадает с верхней частью формулы (32.10). Волны, частоты которых определяются формулами (32.7) и (32.16) по-прежнему являются волнами плотности заряда пучка. Но одна из этих волн нарастает со временем, что свидетельствует о пучковой неустойчивости. Причиной данной неустойчивости является отрицательность диэлектрической проницаемости плазмы. В среде с отрицательной диэлектрической проницаемостью одноименные заряды притягиваются, а разноименные – отталкиваются. Поэтому, если где-то возникают спонтанные сгущения электронов пучка, то они нарастают со временем, что означает самомодуляцию пучка по плотности. Данную неустойчивость называют апериодической пучковой неустойчивостью в среде с отрицательной диэлектрической проницаемостью или неустойчивостью типа отрицательной массы. Термин «апериодическая» означает, что в сис-
теме покоя пучка частота пучковой волны ω − kzu является чисто мнимой величиной. Эта чисто мнимая частота определяется формулой (32.16). Термин «отрицательная масса» имеет свои корни в механике: при замене положительной массы m на − m < 0 частота колебаний пружинного маятника ω = k m становится мнимой, и устойчивые колебания маятника сменяются апериодической раскачкой.
Заметим, что в среде с диэлектрической проницаемостью ε0 < 0 была бы неустойчива любая однородная квазинейтральная система электрических зарядов. Правда, для реализации такой неустойчивости потребовалась бы некая среда, у которой статическая диэлектрическая
150
