
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdfАлександров А.Ф., Кузелев М.В. Физика электронных пучков
Поскольку в металле из-за очень большой (бесконечной) проводимости электрическое поле равно нулю, то из (19.14) следует равенство нулю на границе металла тангенциальной со-
ставляющей вектора Er . Из второго уравнения (19.1) следует условие на разрыв нормальной составляющей вектора напряженности электрического поля E :
E2n − E1n = 4π(σ +σ0 ),
|
2 |
|
|
2 |
|
(19.15) |
|
σ = lim |
ρdl, |
σ0 |
= lim |
∫1 |
ρ0dl, |
||
|
|||||||
1→2 |
∫1 |
|
1→2 |
|
|
где σ − поверхностная плотность зарядов в плазме, а σ0 − поверхностная плотность заряда внешнего источника. Интегрирование в (19.15) производится вдоль нормали к границе раздела сред так, что точка “1” находится в первой среде, а точка “2” – во второй. Из третьего уравнения (19.1) следует условие на разрыв тангенциальной составляющей вектора магнит-
ной индукции B :
r |
r |
|
r |
|
|
4π |
|
r |
r |
|
[n |
(B |
− B )] |
= |
|
|
(i |
+ i |
), |
||
|
|
|||||||||
|
|
2 |
1 |
|
|
c |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
(19.16) |
|
r |
2 |
r |
r |
|
|
2 |
r |
|
||
i = ∫ |
jdl, i0 |
= ∫ |
j0dl, |
|
||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
где i −поверхностная |
плотность плазменного тока, а i0 − поверхностная плотность тока |
|||||||||
внешнего источника.
Обозначим через L характерный пространственный, а через T характерный временной масштабы некоторого исследуемого с помощью уравнений (19.8) нестационарного процесса. Не трудно видеть, что первое и третье уравнения системы (19.8) содержат параметр
L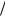 (cT) . Действительно, по порядку величины ∂
(cT) . Действительно, по порядку величины ∂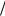 ∂t ~ T −1 , а rot ~ L−1 . Если выполнено силь-
∂t ~ T −1 , а rot ~ L−1 . Если выполнено силь-
ное неравенство |
|
||
|
L |
<<1, |
(19.17) |
|
cT |
||
|
|
|
|
то в нулевом приближении по параметру (19.17) уравнения Максвелла (19.8) можно записать в виде:
r |
|
|
~ |
= 0, |
|
rot E |
(19.18) |
|
r |
~ |
|
~ |
|
|
div E |
= 4πρ, |
|
|
r |
|
|
~ |
|
а переменное магнитное поле B |
в нулевом приближении по параметру (19.17) равно нулю. |
|
Электрическое поле ~r , определяемое из уравнений (19.18), называют потенциальным или
E
электростатическим (хотя статическим поле ~ не является, поскольку, вообще говоря, зави-
E
сит от времени). Нулевое приближение по параметру (19.17), получило название потенциального или электростатического приближения. Неравенство (19.17) означает, что скорость
81
Александров А.Ф., Кузелев М.В. Физика электронных пучков
переноса возмущений в системе мала по сравнению со скоростью света. В дальнейшем мы часто будем пользоваться потенциальным приближением при описании сравнительно медленных процессов в плазме и электронных пучках.
Если ввести скалярный потенциал ϕ так, что |
|
|
|
~ |
|
~ |
~ |
(19.19) |
E |
= − grad ϕ , |
|
то первое уравнение в (19.18) удовлетворится автоматически, а второе – перейдет в уравнение Пуассона
~ |
~ |
(19.20) |
∆ϕ |
= −4πρ . |
|
Заметим, что пренебрегать полями Br |
и B(s) в потенциальном приближении вообще говоря |
|
|
0 |
|
нельзя. Например, вклад внешнего магнитного поля в силу Лоренца определяется цикло-
тронной частотой Ωα = eα B0  mα c частиц сорта α , которая с неравенством (19.17) не связана.
mα c частиц сорта α , которая с неравенством (19.17) не связана.
Уравнения (19.7) для собственных электрического E(s) (rr) и магнитного Br(s) (rr) полей являются уравнениями электростатики и магнитостатики. Для стационарных собственных полей параметр (19.17) равен нулю, поскольку T = ∞. Заметим, что деление электромагнитного поля на собственное стационарное и переменное строго обосновано, если плазма находится в некотором состоянии равновесия, определяемом из уравнений (19.7). При этом уравнения (19.8) описывают динамику плазмы при ее отклонении от равновесного состояния. В общем случае ситуация сложнее, поскольку состояние равновесия может отсутствовать, или оно еще не успело установиться, а поэтому собственные поля зависят от времени. Однако на фоне сравнительно медленной эволюции собственных полей, зарядов и токов в плазме могут развиваться быстро протекающие процессы, описываемые уравнениями (19.8). В этих случаях разделение полей на собственные стационарные и быстро переменные вполне оправдано.
§ 20. Движение заряженных частиц в стационарном нескомпенсированном пучке, находящемся во внешнем магнитном поле
Даже когда пучок в целом стационарен, его собственные поля приводят к сложному движению каждого отдельного электрона. Рассмотрим это на примере бесконечно длинного цилиндрического пучка с равномерно распределенной плотностью заряда, находящегося в однородном аксиальном магнитном поле B0 . Плотность электронов пучка зададим в виде
n |
= const, |
r ≤ r |
(20.1) |
nb (r) = 0b |
|
b |
|
0, |
|
r > rb , |
|
где rb - радиус пучка. Предположим, что заряд электронов частично скомпенсирован одно-
родным фоном бесконечно тяжелых однозарядных ионов, т.е. плотность ионов есть
82
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ni (r) = f nb (r) , где f ≤1- постоянный коэффициент зарядовой нейтрализации. Считаем также, что система имеет осевую симметрию и все характеризующие её величины не зависят от продольной координаты z . Пока ограничимся случаем нерелятивистского пучка.
В принятых условиях электрическое и магнитное поля следует представить в виде E = {Er ,0,0}, B = {0, Bϕ , B0 + Bz }, где Er , Bϕ , Bz - компоненты собственного поля пучка (здесь
и в дальнейшем, если это не приводит к недоразумениям, мы индекс “ (s) ” при записи собст-
венных полей опускаем.). Уравнения движения произвольного электрона пучка в цилиндрических координатах имеют вид
|
dr |
= v |
, |
|
dv |
r |
|
− |
|
vϕ2 |
= |
|
e |
E |
|
+ |
|
e |
|
v |
(B |
+ B |
) − |
e |
v B , |
||||||||||
|
dt |
|
|
|
|
|
|
r |
m |
|
|
mc |
mc |
||||||||||||||||||||||
|
|
r |
|
|
dt |
|
|
|
|
r |
|
|
|
|
ϕ |
0 |
|
z |
|
z |
ϕ |
||||||||||||||
r |
dϕ |
= v |
, |
|
dvϕ |
|
+ |
vr vϕ |
|
= − |
|
e |
|
v |
(B + B |
), |
|
|
|
(20.2) |
|||||||||||||||
dt |
|
|
dt |
|
|
r |
|
|
|
mc |
|
|
|
||||||||||||||||||||||
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
0 |
z |
|
|
|
|
|
||||||||||
|
dz |
= v |
, |
|
dvz |
= |
|
e |
|
v |
|
B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dt |
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
z |
|
|
dt |
|
r |
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Заметим, |
что уравнения для компонент скорости vr , vϕ , vz можно получить из уравнений |
||||||||||||||||||||||||||||||||||
(18.12), отбросив производные по координатам r,ϕ, z |
и заменив частную производную по |
||||||||||||||||||||||||||||||||||
времени на обычную.
Самым простым решением уравнений (20.2) является следующее:
vz = u = const, |
vr = 0, r = const, |
||
dϕ |
|
(20.3) |
|
= ω = const, |
vϕ = ω r. |
||
dt |
|||
|
|
||
Здесь ω - некоторая круговая частота. Согласно решению (20.3) каждый электрон движется вдоль оси z со скоростью u и вращается по круговым орбитам вокруг оси симметрии r = 0 с круговой частотой ω , т.е. весь пучок вращается как целое с угловой скоростью ω . Однако, для применимости решений (20.3) необходимо еще выполнения условия баланса сил (центробежной, электростатического расталкивания и магнитного сжатия), которое следует из второго уравнения системы (20.2):
− |
vϕ2 |
= |
e |
E |
|
+ |
|
e |
v (B |
+ B |
) − |
e |
v B . |
(20.4) |
|
r |
m |
|
|
|
mc |
||||||||||
|
|
|
r |
|
|
mc ϕ |
0 |
z |
|
z ϕ |
|
||||
Компонента Bz собственного магнитного поля пучка обусловлена его азимутальным |
|||||||||||||||
вращением, компонента Bϕ |
связана с продольным движением пучка. Пренебрегая пока соб- |
||||||||||||||
ственным магнитным полем по сравнению с внешним B0 |
(это согласуется с предположением |
||||||||||||||
о том, что пучок нерелятивистский), запишем уравнение баланса сил (20.4) в виде |
|||||||||||||||
− |
vϕ2 |
= |
e |
E |
r |
+ |
|
e |
v B . |
|
|
|
|
(20.5) |
|
r |
m |
|
|
|
|
|
|
||||||||
|
|
|
|
|
mc ϕ |
0 |
|
|
|
|
|
||||
83
Александров А.Ф., Кузелев М.В. Физика электронных пучков
В дальнейшем, конечно, будет учтено и собственное магнитное поле пучка и его релятивизм.
Для нахождения собственного электростатического поля Er используем первое уравнение стационарной системы (19.7), которое в рассматриваемом случае оказывается следующим:
|
1 |
|
d |
rE |
r |
= 4πe(n |
− n ) = 4πe(1− f )n |
0b |
. |
(20.6) |
|
|
|
||||||||
|
r dr |
b |
i |
|
|
|||||
|
|
|
|
|
|
|
||||
Интегрируя (20.6) с граничным условием Er (0) = 0 , находим |
|
|||||||||
|
Er (r) = 2πe(1 − f )n0br, 0 < r < rb . |
|
|
(20.7) |
||||||
Подставляя далее (20.7) в (20.5) и учитывая, что vϕ = ω r (см. (20.3)), получаем следующее уравнение для определения частоты вращения пучка:
ω |
2 − Ω ω + |
1 |
ω2 |
(1 − f ) = 0 . |
|
(20.8) |
|||||
2 |
|
||||||||||
|
|
e |
|
Lb |
|
|
|
|
|||
Здесь ωLb - ленгмюровская частота электронов пучка (см. (16.2)), а Ωe = | e | B0 |
mc - элек- |
||||||||||
тронная циклотронная частота. Из (20.8) находим две частоты вращения пучка |
|
||||||||||
ω |
|
= ω(±) = |
Ω |
|
|
1− |
2ω2 |
|
(20.9) |
||
1,2 |
|
e |
1± |
Lb (1 − |
f ) . |
||||||
|
b |
|
2 |
|
|
Ω2 |
|
|
|||
|
|
|
|
|
|
|
|
e |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
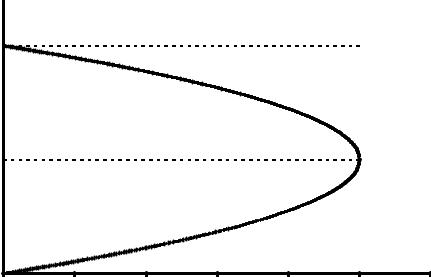
На Рис. 20.1 представлены зависимости частот (20.9) от параметра |
|
||||||||||
|
|
2ω2 |
|
|
|
|
|
|
|
|
|
η |
= |
Lb |
(1 − f ) . |
|
|
|
|
(20.10) |
|||
|
|
|
|
|
|||||||
|
|
Ω2 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
При η >1 частоты ωb(±) становятся комплексными, что свидетельствует об отсутствии ста-
ционарного состояния пучка: при η >1 силы электростатического расталкивания электро-
нов, определяемые величиной ωLb2 (1− f ) , превосходят силы магнитного сжатия (точнее не сжатия, а магнитного удержания электрона на ларморовской орбите), определяемые величи-
ной Ωe2 . В частном случае η =1 , при котором ωb(+) = ωb(−) = Ωe 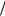 2 , пучок называется бриллю-
2 , пучок называется бриллю-
эновским потоком.
При η = 0 электрический заряд пучка полностью нейтрализован зарядом ионного фо-
на ( f =1). При этом ωb(+) = Ωe , а ωb(−) = 0 , что является очевидным результатом: при наличии только внешнего однородного магнитного поля электрон либо вообще не вращается, либо вращается с электронной циклотронной частотой. Если η <<1, то частоты вращения равны
ωb( |
− |
) ≈ |
ω2 |
cE |
r |
|
ωb( |
+ |
) ≈ Ωe −ωb( |
− |
) , |
|
|
|
Lb |
(1− f ) = |
|
, |
|
|
(20.11) |
||||||
|
|
rB0 |
|
|
|||||||||
|
|
|
2Ωe |
|
|
|
|
|
|
|
|||
где Er определено в (20.7). Первая частота описывает дрейфовое движение электронов в скрещенных собственном электрическом и внешнем магнитном полях. Действительно,
84
Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
ω |
|
|
|
|
|
|
|
|
|
|
|
Ωe |
|
|
|
|
|
|
Ωe |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
η |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
Рис. 20.1
Угловые скорости ωb(±) вращения сплошного нерелятивистского электронного пучка в однородном внешнем магнитном поле
85

|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
согласно |
(4.11) скорость дрейфа равна c[E B] B2 . В нашем случае E = {Er ,0,0}, |
Br = {0,0, B |
}, поэтому скорость дрейфа направлена по азимуту и равна ω(−)r , что и дает пер- |
0 |
b |
вое выражение (20.11). Вторая частота в (20.11) соответствует обычному циклотронному вращению в магнитном поле.
Обобщим проведенное рассмотрение на случай, когда проекция орбиты электрона на плоскость, перпендикулярную вектору внешнего магнитного поля, не является окружностью с центром на оси симметрии. Введем декартовы координаты x, y, z так, что на оси симмет-
рии пучка x = y = 0 . Собственное электрическое поле (20.7) в декартовых координатах за-
пишем в виде (собственное магнитное поле по-прежнему не учитываем):
Er = 2πe(1 − f )n |
|
(x nr |
+ y nr |
), x2 |
+ y2 < r , |
|
|
|
(20.12) |
|||||||
|
0b |
|
x |
y |
|
|
|
|
b |
|
|
|
|
|
|
|
где nrx , nry - единичные векторы декартовой системы в плоскости перпендикулярной оси |
z . |
|||||||||||||||
Уравнения движения электрона в собственном поле (20.12) и внешнем поле Br = {0,0, B nr |
} |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
z |
|
записываются в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(&x& nr |
+ &y& nr |
+ &z&nr |
) = eEr + |
e |
(y&B |
nr |
− x&B nr |
y |
) |
, |
(20.13) |
|||||
|
||||||||||||||||
x |
y |
|
z |
|
|
|
c |
0 |
x |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где точками обозначено дифференцирование по времени. Расписывая (20.13) по компонентам ( e < 0 ), имеем
&x&= |
1 |
|
ω2 |
(1− f )x −Ω |
|
y&, |
|
|
2 |
|
|
||||||
|
|
Lb |
|
e |
|
|
||
&y&= |
1 |
ωLb2 |
(1− f ) y + Ωe x&, |
(20.14) |
||||
2
&z&= 0.
Для решения уравнений (20.14) удобно перейти во вращающуюся систему координат. Введем новые переменные
x′ = x cos ωt + y sin ωt,
(20.15)
y′ = y cos ωt − x sin ωt,
где ω - одна из частот (20.9). Подставляя (20.15) в уравнения (20.14) и учитывая уравнение (20.8), получим следующую систему для новых переменных:
&x&′ = −ωv y&′, |
(20.16) |
|
&y&′ = ωv x&. |
||
|
Здесь ωv = Ωe − 2ωb(±) - так называемая частота вихря. Таким образом во вращающейся систе-
ме координат электрон пучка движется по круговым орбитам с круговой частотой, равной частоте вихря.
Легко видеть, что
86

Александров А.Ф., Кузелев М.В. Физика электронных пучков
| ω |
|
|= ω(+) −ω(−) = Ω |
|
1 − |
2ω2 |
(20.17) |
|
v |
e |
Lb (1− f ) . |
|||||
|
b |
b |
|
Ω2 |
|
||
|
|
|
|
|
|
e |
|
Если возмутить движение электрона, вращающегося с угловой скоростью ωb(±) по круговой орбите с радиусом r и с центром на оси симметрии пучка, то во вращающейся системе его движение будет круговым с периодом 2π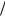 | ωv | (радиус этого кругового движения определя-
| ωv | (радиус этого кругового движения определя-
ется величиной возмущения исходной орбиты). В лабораторной системе координат электрон движется по трохоиде (Рис. 20.2).
87

Александров А.Ф., Кузелев М.В. Физика электронных пучков
O |
Рис. 20.2 |
Траектория возмущенного движения электрона пучка во внешнем магнитном поле
88
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Глава V. Равновесные конфигурации электронных пучков
§ 21. Уравнение баланса радиальных сил
Рассмотрим стационарные равновесные состояния многокомпонентной аксиально симметричной заряженной плазмы, ориентированной вдоль внешнего однородного магнит-
ного поля Br = {0,0, B0 } и состоящей из электронного пучка и заряженных частиц других сор-
тов. Предположим, что плазма бесконечна и однородна вдоль оси z и все характеризующие ее величины зависят только от координаты r (в цилиндрической системе {r,ϕ, z}). Исходим из уравнений многожидкостной гидродинамики (18.7), записанных в форме (18.12).
Поскольку в стационарном равновесном состоянии макроскопическое радиальное движение в плазме отсутствует, гидродинамическую скорость любой ее компоненты можно
представить в виде |
|
Vα (r) = {0, Vαϕ (r), Vαz (r)}. |
(21.1) |
Так как равновесное состояние стационарно ( ∂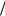 ∂t = 0 ), аксиально симметрично ( ∂
∂t = 0 ), аксиально симметрично ( ∂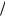 ∂ϕ = 0 ) и
∂ϕ = 0 ) и
однородно вдоль оси z ( ∂ ∂z = 0 ), то при скорости вида (21.1) уравнение непрерывности для каждой компоненты плазмы удовлетворяется автоматически.
∂z = 0 ), то при скорости вида (21.1) уравнение непрерывности для каждой компоненты плазмы удовлетворяется автоматически.
Движение электрических зарядов плазмы в азимутальном направлении (со скоростью
Vαϕ ) создает аксиальное собственное магнитное поле Bz , а движение зарядов в направлении
оси z (со скоростью Vαz ) создает азимутальное собственное магнитное поле |
Bϕ . Поэтому |
полное магнитное поле в системе имеет следующую структуру: |
|
B(r) = {0, Bϕ (r), B0 + Bz (r)}. |
(21.2) |
Собственное электрическое поле следует представить в виде |
|
E(r) = {Er (r), 0, 0}, |
(21.3) |
а электрическое поле внешних источников отсутствует (составляющие собственного поля
Eϕ и Ez могут отличаться от нуля только при неоднородном распределении зарядов по координатам ϕ и z , чего в рассматриваемом сейчас случае нет).
Для нахождения собственных электрического и магнитного полей используем ста-
ционарные уравнения Максвелла (19.7) с материальными уравнениями (19.4) divEr = 4π∑eα Nα (r),
|
|
α |
(21.4) |
|
r |
4π |
r |
||
|
||||
rotB = |
|
∑eα Nα (r)Vα (r). |
|
|
c |
|
|||
|
α |
|
Расписывая с учетом (21.1), (21.2) и (21.3) уравнения (21.4) по компонентам, получим следующие соотношения:
89

|
|
|
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|||
1 |
|
|
d |
rEr (r) = 4π∑eα Nα (r), |
|
||||||
r dr |
|
||||||||||
|
|
|
|
|
|
α |
|
||||
d |
Bz (r) = − |
4π |
|
∑eα Nα (r)Vαϕ (r), |
(21.5) |
||||||
dr |
|
|
|||||||||
|
|
|
c |
α |
|
||||||
1 |
|
|
d |
rBϕ (r) = |
|
4π |
∑eα Nα (r)Vαz (r). |
|
|||
r dr |
|
|
|||||||||
|
|
|
c |
|
α |
|
|||||
Интегрируя (21.5) по r , находим выражения для собственных полей заряженной плазмы
|
|
4π |
|
|
r |
|
|
Er (r) = |
|
|
′ ′ |
′ |
|
||
|
|
|
|
||||
r |
|
∑eα ∫Nα (r )r dr , |
|
||||
|
|
|
α |
0 |
|
|
|
Bz (r) = |
|
4π |
|
∑eα |
∞∫Nα (r′)Vαϕ (r′)dr′, |
(21.6) |
|
|
c |
||||||
|
|
|
α |
r |
|
|
|
|
|
4π |
|
|
r |
|
|
Bϕ (r) = |
|
|
′ |
′ ′ |
′ |
||
cr |
|
∑eα ∫Nα (r )Vαz (r )r dr . |
|||||
|
|
|
α |
0 |
|
|
|
Обратим внимание на пределы интегрирования в выражениях (21.6). При интегрировании соотношений (21.5) возникают произвольные константы, для определения которых используются очевидные граничные условия:
Er (0) = 0, Bz (∞) = 0, Bϕ (0) = 0 . |
(21.7) |
Легко видеть, что функции (21.6) удовлетворяют именно этим граничным условиям, что и обусловило выбор пределов интегрирования в (21.6).
Перейдем теперь к рассмотрению уравнения баланса сил. Подставляя в стационарные уравнения (18.12) представления (21.1), (21.2) и (21.3), получим единственное для каждой компоненты системы уравнение баланса радиальных сил
− |
Vαϕ2 |
= |
|
e |
|
1− |
V |
2 |
− |
Vαϕ2 |
|
E |
|
+ |
1 |
V |
(B |
+ B |
) − |
1 |
V B |
|
, |
(21.8) |
||||||
|
|
|
α |
|
αz |
|
2 |
|
r |
|
|
|
|
|||||||||||||||||
|
r |
|
mα |
|
|
|
c |
2 |
|
|
c |
|
|
c |
αϕ |
0 |
z |
|
c |
αz ϕ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
а баланс сил в направлениях z |
|
и ϕ удовлетворяется тривиально, т.е. 0 = 0. Вводя обычные |
||||||||||||||||||||||||||||
обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
βαϕ (r) = |
Vαϕ |
(r) |
, |
βαz (r) = |
V |
|
(r) |
, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
αz |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(21.9) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
||||
γα (r) = (1 − βα2z (r) − βαϕ2 (r))−1 2 , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
запишем уравнение (21.8) в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
− mα c2γα (r) |
βαϕ2 (r) |
= eα [Er (r) + B0 βαϕ (r) + Bz (r)βαϕ (r) − Bϕ (r)βαz (r)]. |
(21.10) |
|||||||||||||||||||||||||||
|
|
r |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И наконец, подставляя в (21.10) выражения (21.6), получим следующее уравнение баланса радиальных сил:
90
