Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

Аппаратные средства вычислительной техники

Файл:

27_VaN[1]

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

4.53 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Александров А.Ф., Кузелев М.В. Физика электронных пучков

пучка, каких-либо ограничений на величину его тока нет. На самом деле это не так: как уже отмечалось выше, значение тока ограничивает ряд неустойчивостей. Если пучок полностью замагничен, то таких неустойчивостей две: неустойчивость Пирса и неустойчивость Бунемана. Вторая из них, обусловленная движением ионов, будет рассмотрена в следующей главе. Сейчас же рассмотрим обусловленную конечным продольным размером дрейфового пространства неустойчивость Пирса. Учет движения нейтрализующих пучок ионов в теории неустойчивости Пирса не существенен.

Неустойчивость Пирса тесно связана со свойствами волн плотности заряда пучка, которые в простейшем одномерном нерелятивистском случае имеют спектры (27.7)

ω = kzu ±ωLb .	(29.1)
Видно, что при kz = ωLb u	медленная волна является стационарной (ω = 0 ). Стационарное

электрическое поле этой волны в пространстве дрейфа, ограниченном в направлении движения пучка, оказывает сильное воздействие на электроны, что и приводит при определенных условиях к неустойчивости.

Рассмотрим безграничный в поперечном направлении пучок, движущийся вдоль оси OZ от металлической плоскости z = 0 к металлической плоскости z = L . Обе плоскости заземлены. Стационарное возмущение плотности заряда пучка в медленной волне (29.1) имеет

вид
~	ωLb
enb (z) = en sin			z ,	(29.2)
enb (z) = en sin		u	z ,	(29.2)
		u

где n~ - некоторая амплитуда. При записи (29.2) учтено, что в плоскости инжекции z = 0 пучок не возмущен. Заряды (29.2) наводят статические заряды на металлических плоскостях. Наведенные заряды в свою очередь создают стационарное электрическое поле, которое однонаправлено действует на электроны пучка и сильно возмущает их движение.

Вычислим наведенные поля. Из уравнения Пуассона с граничными условиями

d 2ϕ

= −4πen (z),

ϕ(0) = ϕ(L) = 0

(29.3)

dz2

с учетом (29.2) имеем

ωLb

ϕ(z) = 4πen

sin

−

sin

L .

(29.4)

ωLb

Первый член в (29.4) есть потенциал поля пучковой волны, а второй член определяет наведенное поле. Изменение скорости электронов пучка, обусловленное наведенным полем, вычисляется из уравнения движения

131

Александров А.Ф., Кузелев М.В. Физика электронных пучков

(29.5)

n0b L u

sin

Lb L ,

анализ которого дает необходимую информацию об устойчивости системы.

Пусть

или

sin

Lb L > 0,

(29.6)

ωLb

2πs <

L < 2π(s +1 2), s = 0,1,2,K .

При этом,

если

> 0

(возмущение

(29.2) представляет собой избыток

электронов), то

dv dt > 0 и наведенное поле ускоряет электроны,

т.е. действует в сторону уменьшения n , и

(недостаток электронов), то

избыток электронов уничтожается. Если n < 0

dv dt < 0 и наве-

денное поле действует в сторону увеличения

, т.е. уничтожает недостаток электронов.

Следовательно, в условиях (29.6) пучок устойчив. Пусть теперь

или

sin

Lb L < 0,

(29.7)

ωLb

2π(s +1 2) <

L < 2π(s +1),

s = 0,1,2,K .

Тогда dv~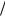dt < 0 при n~ > 0 , т.е. наведенное поле тормозит электроны, что приводит к росту избытка электронов n~ . Если же n~ < 0 , то dv~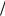dt > 0 , и недостаток электронов нарастает. Та-

ким образом, в условиях (29.7) пучок неустойчив. Как видно из уравнения (29.5), характерное время развития неустойчивости (время, за которое v~ становится порядка u , а n~ - по-

рядка n0b ) может быть оценено по формуле

τ =

−1

sin

(29.8)

Lb u

Таким образом, время развития и насыщения неустойчивости Пирса по порядку величины совпадает с временем пролета электроном пучка дрейфового пространства.

Проведенный качественный анализ позволил только установить факт неустойчивости, найти условия ее возникновения и оценить время ее развития. К чему приводит неустойчивость пока неясно; так, число электронов в области 0 < z < L может нарастать, но может и уменьшаться. Ниже изложены строгая линейная теория неустойчивости Пирса и нелинейная теория, из которой будет видно, что в дрейфовом пространстве большой длины неустойчивость Пирса приводит к сильному искажению тока пучка, вплоть до его полного срыва.

Принципиальным для развития неустойчивости Пирса является существование стационарных в лабораторной системе отсчета волн плотности заряда пучка, причем (29.7) есть условие положительной обратной связи, когда наведенные в межэлектродном промежутке

132

Александров А.Ф., Кузелев М.В. Физика электронных пучков

поля способствуют дальнейшему росту возмущений плотности, эти поля создавших. Порог развития неустойчивости, как это следует из (29.7), имеет вид (с учетом релятивизма пучка)

ω	Lb γ −3 2		(29.9)
	Lb γ −3 2	L ≥ π ,	(29.9)
u

т.е. определяется длиной дрейфового пространства. Соотношение (29.9) можно переписать и по-другому:

kz (0)L ≥π , (29.10)

где kz (0) - волновое число пучковой волны при нулевой частоте. Оказывается, что (29.10)

является существенно более общим условием, чем (29.9). Действительно, с учетом конечного поперечного размера пространства дрейфа и при однородной в поперечном сечении плотности пучка спектры пучковых волн плотности заряда определяются из дисперсионного уравнения (28.10). Из этого уравнения имеем:

kz (0) = k 1 αПирса −1 .	(29.11)
Из (29.11) видно, что при αПирса <1 действительного kz (0)	нет (точнее kz (0) = 0 ), а следова-

тельно, не существует и стационарной пучковой волны. Такая волна существует только при выполнении неравенства (28.13), а поэтому только при αПирса >1 и возможно развитие неус-

тойчивости Пирса. Дисперсионные кривые пучковых волн плотности заряда для различных параметров Пирса представлены на Рис. 28.1.

Существование стационарных пучковых волн необходимо для развития неустойчивости Пирса, поэтому условие (28.13) называют необходимым условием данной неустойчивости. Полное же условие неустойчивости, следует из (29.10) и (29.11) и имеет вид

αПирса ≥1+	π 2		ω2	γ −3	≥ k 21 +	π 2
		или	Lb	2		2 .	(29.12)
	2 2
	k 1L		u			L

Или в более общей форме, по типу (29.7), полное условие неустойчивости Пирса с учетом конечного поперечного размера пространства дрейфа записывается следующим образом:

2π(s +1 2) < k 1L αПирса −1 < 2π(s +1), s = 0,1,2,K .	(29.12а)
В длинных системах, когда k 1L >>1 (или L >> R )	полное условие неустойчивости

фактически сводится к необходимому условию (28.13). Причем необходимое условие в виде

αПирса ≥1

(29.13)

справедливо при любой поперечной геометрии пучка, если он только полностью замагничен. В предыдущем параграфе, определяя пирсовские токи (28.16), (28.18) и (28.19), мы использовали необходимое условие неустойчивости Пирса в форме (29.13). Именно эти токи и называются предельными токами скомпенсированных по статическому заряду электронных

133

Александров А.Ф., Кузелев М.В. Физика электронных пучков

пучков. Устойчивая (стабильная) транспортировка пучков с большими токами невозможна. Получим наиболее общее выражение для параметра Пирса полностью замагниченного электронного пучка. Для этого в интегральном уравнении (28.19) положим ω = 0 , а затем

совершим предельный переход kz → 0 . В результате получим следующее однородное инте-

гральное уравнение Фредгольма 2-го рода:

ω2 γ −3 ∞

k 2 ϕ (rr )

j (r )=

k 2 u2

∑n=1 k 2

∫∫Pb (r )ϕn (r )j

(r )dr .

Минимальное собственное значение интегральной задачи (29.14)

ωLb2 γ −3 = λ

k 21u2 min

(29.14)

(29.15)

и определяет искомый параметр Пирса согласно следующей формуле:

α		≡	ω	2	γ −3		.	(29.16)
	Пирса			Lb
			k 2 u2λ			min
			k 2 u2λ
			1

Для сплошного и бесконечно тонкого пучков из (29.16) следуют выражения (28.13) и (28.15). Вернемся теперь к формуле (26.12), определяющей предельный вакуумный ток бес-

конечно тонкого электронного пучка, и перепишем ее для γ >>1 в виде
Ib0 = I0γGb .	(29.17)
В этой формуле γ = γ0 - релятивистский фактор электрона в плоскости инжекции,	т.е. при

z = 0 . В прошедшем в дрейфовое пространство пучке при z → ∞ релятивистский фактор меньше и определяется выражением (26.11): γ∞ = γ13 . В формуле же (28.16), поскольку ста-

тический заряд пучка нейтрализован, γ есть релятивистский фактор как в плоскости инжек-

ции, так и в прошедшем пучке. То есть формулу (28.16) можно переписать в виде ( u ~ c )

I	Пирса	= I	0	γ 3 G .		(29.18)
	Пирса		0	∞	b

Если теперь в (29.17) выразить релятивистский фактор γ через релятивистский фактор про-

шедших в пространство дрейфа электронов - γ = γ∞3 , то получим (29.18). Следовательно,

справедливо утверждение: если в вакуумное дрейфовое пространство инжектируется ультрарелятивистский тонкий пучок с током, равным предельному вакуумному току, то в пространстве дрейфа вдали от места инжекции этот же ток оказывается равным току Пирса.

§ 30. Линейная теория неустойчивости Пирса

Неустойчивость скомпенсированного электронного пучка, ограниченного заземленными электродами, в одномерном и потенциальном приближении впервые была исследована Пирсом. Изложим здесь соответствующую теорию, придерживаясь наиболее ранних работ в

134

Александров А.Ф., Кузелев М.В. Физика электронных пучков

этой области. Как и в § 27 исходим из следующих линеаризованных одномерных нерелятивистских уравнений потенциального приближения (см. систему (27.2)):

	~		~			~
	∂Nb	+ u	∂Nb	= −n		∂Vbz		,
	∂t		∂z		0b	∂z
	~		~		e	~
	∂Vbz + u		∂Vbz	= −	e	∂ϕ	,	0 < z < L,	(30.1)
	∂Vbz + u		∂Vbz	= −		∂ϕ	,	0 < z < L,	(30.1)
	∂t		∂z		m ∂z
	2 ~		~
	∂ ϕ		~
	∂z2	= −4πeNb .
Здесь	~		~	~			-	возмущения скорости,	плотности и скалярного потенциала.
Здесь	Vbz (z,t),		Nb (z, t), ϕ(z, t)				-	возмущения скорости,	плотности и скалярного потенциала.

Уравнения (30.1) следует дополнить граничными условиями на металлических электродах z = 0 и z = L :

~		~
Nb (0,t) = 0,		Vbz (0,t) = 0,	(30.2)
~	~
ϕ	(0,t) =ϕ(L,t) = 0.

Первые два условия в (30.2) означают, что в межэлектродное пространство инжектируется невозмущенный пучок, вторые два означают, что электроды заземлены.

Задача (30.1) – (30.2) является однородной по времени t , но неоднородной по координате z . Метод решения подобных задач состоит в следующем. Возмущенные величины представляются в виде

(30.3)

Vbz (z, t) =V (z) exp(−iωt), Nb (z, t) = N (z) exp(−iωt),

ϕ(z, t) = ϕ(z) exp(−iωt) ,

где ω - некоторая частота. Подставляя (30.3) в (30.1), для функций V (z), N(z), ϕ(z)

имеем

следующие уравнения:

−iωN + u

= −n

∂z

−iωV + u

= −

dϕ

(30.4)

m ∂z

d 2ϕ2 = −4πeN. dz

Общее решение системы однородных обыкновенных дифференциальных уравнений (30.4) находится как суперпозиция всех линейно независимых решений и имеет вид:

ϕ(z) = Aexp(ikz1 (ω)z)+ B exp(ikz 2 (ω)z)+ Cz + D,
V (z) = −			e		[Akz1 (ω) exp(ikz1 (ω)z)− Bkz 2 (ω) exp(ikz 2 (ω)z)]−i	e	C,	(30.5)
						mω
			mωLb
N(z) =		1		[Akz21 (ω) exp(ikz1 (ω)z)+ Bkz22 (ω) exp(ikz 2 (ω)z)].
	4πe

Здесь kz1,2 (ω) = (ω ±ωLb )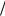u - решения дисперсионного уравнения (27.6) продольных пучко-

вых волн плотности заряда относительно волнового числа kz . Заметим, что в выражении для

135

Александров А.Ф., Кузелев М.В. Физика электронных пучков

амплитуды потенциала ϕ(z) фигурирует линейное слагаемое Cz + D , описывающее поле на-

веденных на электродах зарядов. Действительно, линейное слагаемое удовлетворяет уравнению Пуассона. Кроме того, система уравнений (30.4) имеет не второй, а четвертый порядок,

что, вместо (27.6), дает дисперсионное уравнение kz2ε l (ω, kz ) = 0 . Два решения этого уравне-

ния

соответствуют

пучковым

волнам:

kz1,2 = (ω ±ωLb ) u , а

два другие

вырожденные:

kz3,4

= 0 . Они то и порождают линейную добавку в потенциал.

Подставляя (30.5) в граничные условия (30.2) и исключая постоянные

A, B, C и D ,

получим следующее дисперсионное уравнение для определения частоты ω :

y2 (y2 − x2 )− 2iyx2 (1 − exp(iy) cos x)+ x(y2 + x2 )exp(iy) sin x = 0 ,

(30.6)

где

y = ωL u ,

x = ωLb L u .

(30.7)

Покажем,

что уравнение (30.6) имеет решения относительно частоты ω с положи-

тельной мнимой частью, т.е. ω = ω′ + iω′′

и ω′′ > 0 . Поскольку решение уравнений (30.1) ис-

калось в виде (30.3), то при ω

′′

> 0 оно будет нарастать со временем как exp(ω t) , что озна-

чает неустойчивость системы.

При sin x = 0 , т.е. при

x = xs

= π(2s +1),

s = 0,1,2,K

(30.8)

уравнение (30.6)

имеет решение y = 0 . Полагая

x = xs

+ x′, где | x′| <<1 и учитывая, что в

этом случае и | y | <<1, из уравнения (30.6) имеем:

y = i

x′

= i

− xs ),

или ω = i

(2s +

π(2s +

1) ωb −

1) .

(30.9)

Из (30.9) следует, что при ωb > (u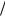L)π(2s +1) мнимая часть частоты ω′′ > 0 , что означает на-

личие неустойчивости.

В общем случае уравнение (30.6) решается только численно. Приведем здесь численные решения уравнения (30.6), полученные в предположении, что величина y чисто мнимая,

т.е. y = i Im y , Re y = 0 . Что такие решения существуют, подтверждают результаты числен-

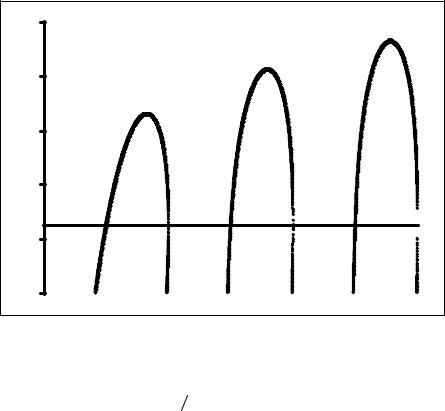
ного решения, представленные на Рис. 30.1. Наличие же решений с отличной от нуля действительной частью ( Re y ≠ 0 ) не исследовалось. Из Рис. 30.1 видно, что области неустойчиво-

сти совпадают с определенными выражениями (29.7). Формулы (30.9) дают значения инкрементов около левых границ каждой из областей неустойчивости (на Рис. 30.1 – около точек x = π, 3π, 5π и т.д.). Из Рис. 30.1 также следует, что максимальные значения Im y по поряд-

ку величины близки к единице (по крайней в области значений параметра x , поместившейся

136

Александров А.Ф., Кузелев М.В. Физика электронных пучков

1.5y

1.1

0.7

0.3

-0.1 0

3.14

6.28

9.42

12.56

15.7

18.84

-0.5

Рис. 30.1

Безразмерный инкремент неустойчивости Пирса y = Imω L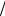u в зависимости от параметра x = ωb L u (одномерное приближение)

137

Александров А.Ф., Кузелев М.В. Физика электронных пучков

на рисунке). Следовательно, характерное время развития неустойчивости Пирса близко к времени пролета пучком дрейфового пространства, что согласуется с (29.8).

§ 31. Нелинейная динамика неустойчивости Пирса

На нелинейной стадии развития неустойчивости Пирса происходят существенные изменения в структуре транспортируемого электронного пучка. Поэтому адекватное рассмотрение нелинейной динамики этой неустойчивости возможно только численными методами. В связи с этим изложим основы методов численного моделирования систем заряженных частиц, описываемых бесстолкновительными кинетическими уравнениями Власова.

Будем исходить из фазовой плотности частиц сорта α , определяемой формулой

Nα (t, rr, pr)= ∑δ (rr − rrj (t))δ (pr − prj (t)),	(31.1)
j

где j − номер частицы, а координата и импульс движения

drrj			r
		= v j		,
		= v j		,
	dpdtrj		= e Er		(t, rr ) +	1	[vr	j	Br(t, rr )] ,
			= e Er		(t, rr ) +		[vr		Br(t, rr )] ,
	dt				j	c			j
	dt					c

j − ой частицы определяются из уравнений

(31.2)

дополненных соответствующими начальными условиями. Фазовая плотность (31.1) есть микроскопическая функция распределения частиц. Одночастичная же функция распределения, которая является решением уравнения Власова, получается из (31.1) в результате усреднения. Процедура усреднения, рассматриваемая в кинетической теории, нами здесь не обсуждается. Фазовая плотность (31.1) определяет плотности заряда и тока частиц сорта α (микроскопические) по формулам

ρα (t, rr)= eα ∫Nα (t, rr, pr)dpr,

rjα (t, rr)= eα ∫vrNα (t, rr, pr)dpr, (31.3)

которые, после подстановки в них (31.1), дают следующее:

ρα (t,rr)= eα ∑δ (rr − rrj (t)),

r	r		(t)		(31.4)
	p
jα (t,rr)= eαc∑	2	2j	2	(t)	δ (rr − rrj (t)).
j	mαc		+ pj

Последние два соотношения являются материальными уравнениями при описании частиц с помощью фазовой плотности (31.1).

При практическом использовании материальных уравнений (31.4) возникает проблема регуляризации входящих в них δ -функций (процедура “размазывания”). Регуляризация

138

Александров А.Ф., Кузелев М.В. Физика электронных пучков

обычно осуществляется согласовано со способом решения уравнений электромагнитного поля. Все это составляет суть метода крупных частиц, имеющего большое число различных модификаций.

В качестве примера рассмотрим регуляризацию выражений (31.4) в случае прямоли-

нейного полностью замагниченного тонкого электронного пучка ( Sb −площадь поперечного сечения пучка, rrb − его средний радиус). Введем продольный размер области регуляризации h . Он может быть как-то связан с шагом разностной сетки для уравнений поля, или с длиной волны, или с длиной всей системы и т.п. Поскольку у электронов тонкого пучка поперечные координаты совпадают, то

δ (rr − rr	(t))=δ (rr	− rr )δ (z − z		(t)).	(31.5)
j		b	j

Осуществим регуляризирующую функции δ(z − z j ) в соответствии со следующим правилом

hδ (z − z j (t))→	1		h2		≡ ∆(		z − z j	).	(31.6а)
	1		h2

	π	h2 + (z − z j )2
Возможны и другие варианты регуляризации. Например,
			z − z j	≤ h		≡ ∆(z − z j ).
hδ(z − z j (t))→ 1,			z − z j	≤ h	2	≡ ∆(z − z j ).			(31.6б)
	0,		z − z j	> h	2

Пусть далее n0b − невозмущенная плотность частиц в электронном пучке. Обозначим через

N = Sbhn0b − полное число электронов в невозмущенном пучке на длине регуляризации h .

Тогда с учетом (31.5) и (31.6) материальные уравнения (31.4) можно записать в виде

ρb (t, rr)= en0b Sbδ(rr

− rrb )

∑∆(

z − z j (t)

prj (t)

(31.7)

r r

∆(z − z j (t)).

jb (t, r )= en0bcSbδ(r − rb )

∑

(t)

m2 c2

+ p2

Макроскопическое

усреднение,

помимо

замены (31.6), осуществляется

оператором

N −1 ∑(...) , причем N является числом крупных частиц и, очевидно, не связано с реальным

числом электронов в каком-либо объеме. Что касается конструкции Sbδ (rr − rrb ), то ее обра-

ботка осуществляется в соответствии с методом решения уравнений поля в поперечном направлении и сложности, как мы сейчас в этом убедимся, не представляет.

Применим изложенный метод крупных частиц для моделирования нелинейной динамики неустойчивости Пирса. Рассмотрим однородный в поперечном сечении прямолинейный электронный пучок, пронизывающий цилиндрическое пространство дрейфа с радиусом R и длиной L . Ограничиваясь потенциальным приближением, исходим из следующих

139

Александров А.Ф., Кузелев М.В. Физика электронных пучков

уравнения и граничных условий для скалярного потенциала ϕ(t, r, z) :

1 ∂

r ∂ϕ +

∂2ϕ = −4π(ρ

− ρ

r ∂r

(31.8)

∂r

∂z2

r=R = ϕ

z=0 = ϕ

z=L = 0.

Здесь ρb - плотность заряда электронного пучка, а ρ0 -

плотность заряда компенсирующего

фона бесконечно тяжелых ионов. Можно, очевидно, считать, что

ρ0 = ρb

t=0 ,

(31.9)

если при t = 0 любые возмущения в пучке отсутствуют.

Для решения уравнения (31.8) применим метод разложения по собственным функциям поперечного сечения пространства дрейфа, а именно, запишем

p
ϕ(t, r, z) = ∑ϕn (t, z)J0 (k nr) ,	(31.10)

n=1

где k n = µ0n 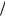R . Число слагаемых p в (31.10) определяется из соображений точности при вычислении потенциала. Функции ϕn (t, z) , как это видно из (31.8), удовлетворяют следую-

щим уравнениям:

∂2ϕ2n	= k 2nϕn − 4πNn−2 ∫R r(ρb − ρ0 )J0	(k nr)dr,
∂z	0	(31.11)

ϕn z=0 = ϕn z=L = 0,

где Nn2 = R2 J12 (µ0n )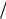2 - нормы функций Бесселя.

В радиальном направлении сплошной электронный пучок следует моделировать слоями (поперечное расслоение пучка происходит из-за поперечной неоднородности поля). Границы слоев зададим в виде 0 = r0 < r1 < r2 <K< ri <K< rq = R , всего q слоев, а i - номер

слоя. Если
k p (ri − ri−1 ) <<1,	(31.12)
то внутри слоя ρb = ρbi и не зависит от координаты r . Таким образом, параметр	p в разло-

жении (31.10) оказывается связанным с толщиной слоя ri − ri−1 , i =1,2,K, q , которую мы здесь считаем постоянной.

Переходя в (31.11) от интегрирования по r к суммированию по слоям и заменяя точ-

ную норму Nn сеточной, перепишем уравнение (31.11) следующим образом:

2	q
∂ ϕ2n	= k 2nϕn − 4π∑σin (ρb − ρ0 )i , n =1,2,K, p .	(31.13)
∂z	i=1

Здесь весовые множители σin даются выражениями

140

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 2914 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке ЭЛТ

#
29.03.20164.53 Mб3427_VaN[1].pdf
#
29.03.2016116.12 Кб20Мониторы с ЭЛТ лекция.mht
#
29.03.20166.45 Кб22Схема монитора с ЭЛТ.gif
#
29.03.201634.05 Кб21Устройство кинескопа.jpg
#
29.03.2016133.55 Кб21Устройство монитора на ЭЛТ.jpg
#
29.03.201622.05 Кб22Устройство ЭЛТ.gif