Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

Аппаратные средства вычислительной техники

Файл:

27_VaN[1]

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

4.53 Mб

Скачать

☆

<<< < Предыдущая 12 / 292 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Александров А.Ф., Кузелев М.В. Физика электронных пучков

где α - начальная фаза, определяемая из начальных условий. Из начальных условий опреде-

ляются также компоненты скорости v и v\|\| , или полная скорость v0 и угол β							между на-
правлениями начальной скорости и магнитного поля
β = arctan(v v\|\| ) .							(3.7)
Подставляя (3.6) в уравнение (1.3) и выполняя интегрирование, найдем координаты
заряда, движущегося в однородном магнитном поле
x = x0 + ρe sin(Ωet +α),						y = y0 + ρe cos(Ωet +α), z = z0 + v\|\|t ,	(3.8)
где
v		v mc		2	−1 2
v		v mc		v0		-	(3.9)
ρe = Ω	e	= eB	1	− c2		-	(3.9)
	e	0

ларморовский радиус заряженной частицы.

Из (3.8) видно, что заряд в однородном магнитном поле движется по винтовой линии с осью вдоль силовой линии поля и с радиусом ρe . Шаг винтовой линии определяется фор-

мулой

2π		mc		2	−1 2
2π		mc		v0		v0 cos β .	(3.10)
he = v\|\|Te = v\|\| Ω	e	= 2π eB	1	− c2		v0 cos β .	(3.10)
	e	0
При v\|\| = 0 , β = π 2 , шаг he = 0 ,				и заряд движется по окружности радиуса ρe			в плоскости
перпендикулярной к магнитному полю.

§4. Движение в постоянных однородных электрическом

имагнитном полях

Рассмотрим теперь движение заряженной частицы при одновременном наличии однородных постоянных электрического и магнитного полей. Ограничимся нерелятивистским случаем, когда v << c и можно использовать уравнение движения (1.4). Условие применимо-

сти нерелятивистского приближения будет установлено позже.

Координатные оси направим так, чтобы было B0 ={0,0, B0},

E0 ={0, E0 y , E0 z }, т.е. ко-

ординатная плоскость

проходит через векторы B0 и E0 . Тогда из уравнений (1.4) и (1.3)

имеем

d 2 x

= ω

dt2

d 2 y

= −ω

0 y

(4.1)

dt2

d 2 z

0 z

dt2

Александров А.Ф., Кузелев М.В. Физика электронных пучков

где ωe - нерелятивистская циклотронная частота (3.2). Из этих уравнений видно, что движе-

ние вдоль оси z и движение в плоскости xy происходят независимо друг от друга (в реляти-

вистском случае это будет не так, что приведет к существенному усложнению задачи). В ча-

стности, из третьего уравнения системы (4.1) следует, что вдоль оси z							заряд движется равно-
ускоренно, т.е.
z =	eE0 z	t2	+ v0 zt + z0 ,	vz =	eE0 z	t + v0 z ,	(4.2)

	2m				m

где v0 z и z0 - постоянные интегрирования.

Первые два уравнения в (4.1) образуют замкнутую систему. Для ее решения сделаем

замену

x = x′+V0d t,

V0d =

eE0 y

= c

E0 y

(4.3)

mωe

′

Относительно переменных x , y первые два уравнения в (4.1) запишутся в виде

d 2 x′

= ω

dt2

(4.4)

d 2 y

dx′

= −ω

dt2

e dt

вообще не содержащем электрического поля. Поскольку уравнения (4.4) совпадают с первыми двумя уравнениями (3.4), то по аналогии с (3.8) сразу запишем решения

x′ = x0 + ρe sin(ωet +α), y = y0 + ρe cos(ωet +α) ,		(4.5)
где ρe = v ωe . Переходя далее от x′	к x , получим окончательно следующее:
x = x0 + ρe sin(ωet +α) +V0d t,	y = y0 + ρe cos(ωet +α) .	(4.6)

Решение (4.6) описывает наложение двух движений: вращение в плоскости xy по ларморов-

ской окружности радиуса ρe с циклотронной частотой ωe и равномерное прямолинейное

движение вдоль оси x со скоростью V0d , называемой скоростью электрического дрейфа. Фи-

зическая причина дрейфа состоит в том, что на противоположных сторонах ларморовской окружности скорость движения заряда различна, из-за ускоряющего (на одной стороне) и тормозящего (на другой стороне) действия электрического поля.

Выберем постоянные интегрирования в (4.6) так, чтобы при t = 0 было x = y = 0

x = ρe sin ωet +V0d t, y = ρe (cosωet −1) .

(4.7)

Зависимости (4.7) задают в параметрической форме циклоиду. Чтобы удобнее проанализировать вид этой кривой введем безразмерные переменные

τ = ωet, ξ =	ωe	x,	ζ =	ωe	y,	µ =		v	,	(4.8)

	V0d			V0d			V0d

Александров А.Ф., Кузелев М.В. Физика электронных пучков

в которых траектория заряда запишется в виде
ξ = µ sinτ +τ, ζ = µ(cosτ −1) .	(4.9)
При µ = 0 траектория - прямая линия, параллельная оси	x ; при µ <1 – укороченная цик-

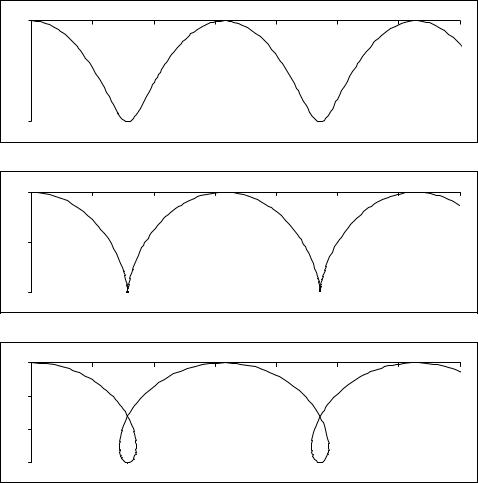
лоида (Рис. 4.1а); при µ =1 - обычная циклоида (Рис. 4.1б); при µ >1 - удлиненная циклоида

(Рис. 4.1в). Чем больше параметр µ , тем сильнее циклотронное вращение и меньше элек-

трический дрейф, и наоборот.

Проведенное в данном параграфе рассмотрение справедливо при выполнении неравенства v << c , где v - скорость любого из движений, в которых участвует заряженная части-

ца. В частности должно быть v << c и vz << c . Относительно дрейфового движения условие

применимости нерелятивистского рассмотрения V0d << c сводится к неравенству
E0 y	B0 <<1.			(4.10)
Не трудно видеть, что в векторной форме скорость электрического дрейфа в скрещен-
ных однородных электрическом и магнитном полях дается формулой
Vr	= c	[Er0 Br0 ]	.	(4.11)

0d		B2
	0

Примечательно, что дрейфовая скорость (4.11) не зависит (и по величине и по направлению) ни от заряда, ни от массы частицы. Это связано с тем, что ускорение, сообщаемое заряду электрическим полем пропорционально em , это же отношение содержит и циклотронная частота ωe .

§ 5. Движение в медленно меняющемся магнитном поле. Адиабатический инвариант

Если магнитное поле медленно меняется в пространстве и времени, то будут изме-

няться и основные характеристики движения заряженной частицы: циклотронная частота ωe ,

ларморовский радиус ρe , продольная v|| и поперечная v скорости, координаты центра лар-

моровской окружности x0 , y0 (см. формулы (3.8)). Медленность означает, что за период цик-

лотронного вращения Te				= 2π ωe на расстоянии ларморовского радиуса ρe	индукция маг-
нитного поля меняется мало. Это предполагает выполнение неравенств
T dB dt <<1,		ρ	e	gradB <<1.	(5.1)
e	B			B

Очевидно, что если неравенства (5.1) нарушены, то вводить перечисленные выше характери-

стики движения заряда (ωe , ρe ,...) вообще не имеет смысла. В этом и следующем параграфах

Александров А.Ф., Кузелев М.В. Физика электронных пучков

0							ξ
0	2	4	6	8	10	12	14
-1	ζ						а

0							ξ
0	2	4	6	8	10	12	14
-1
-2	ζ						б
							б

0							ξ
0	2	4	6	8	10	12	14
-1
-2
-3	ζ						в

Рис. 4.1

Траектории заряда в однородных постоянных взаимно перпендикулярных электрическом и магнитном полях

Александров А.Ф., Кузелев М.В. Физика электронных пучков

будет рассмотрено движение заряженной частицы в магнитном поле, удовлетворяющем неравенствам (5.1).

Введем еще одну характеристику движения заряда в постоянном однородном магнитном поле – магнитный момент. Магнитным моментом плоского контура с током называется вектор

r	1	r
µ =		ISn ,	(5.2)
	c
где I - ток в контуре,			S - площадь поверхности, ограниченной контуром, а nr- единичный

вектор нормали к поверхности, составляющий с направлением обтекания контура током, правовинтовую систему. Можно ввести и магнитный момент заряда, вращающегося по лар-

моровской орбите в магнитном поле. Действительно: если радиус орбиты равен ρe , то

S = πρ2	, если период обращения заряда e по орбите есть T , то						I = e T	. Тогда для модуля
e						e	e
магнитного момента заряда имеем
µe = IS =		eπρ	2	mv2 2	=	W		(5.3)
µe = IS =		cTe	e =		=	,		(5.3)
		cTe		B		B

где W - энергия поперечного движения заряженной частицы. Определим теперь направле-

ние магнитного момента заряда в магнитном поле. Направление вращения заряда (а значит и направление тока) зависит от знака заряда и от направления поля. Пусть вектор Br направлен от читателя в плоскость страницы. Тогда при e > 0 заряд вращается в плоскости страницы против часовой стрелки, против часовой стрелки направлен и ток. При e < 0 заряд вращается по часовой стрелке, а ток по-прежнему направлен против. Следовательно, единичная нормаль nr, составляющая с направлением тока правовинтовую систему, направлена к читателю из плоскости страницы, т.е. противоположна вектору B . Отсюда и из (5.3) окончательно находим

r	W	r	W	r
µe = −		B = −		b	,	(5.4)
	B2		\| B \|

где br- единичный вектор в направлении вектора магнитной индукции.

Магнитный момент заряженной частицы (5.4) может быть введен и в том случае, когда магнитное поле изменяется в пространстве настолько медленно, что выполнено второе неравенство (5.1). Действительно, магнитный момент (5.4) по определению характеризует заряд, находящийся в данной точке пространства. В свою очередь размер области локализа-

ции заряда в магнитном поле равен ρe . Но в силу второго неравенства (5.1) в области разме-

ром ρe магнитное поле следует считать однородным, что и позволяет строго определить магнитный момент заряженной частицы. В неоднородном магнитном поле при перемещении

Александров А.Ф., Кузелев М.В. Физика электронных пучков

заряда в пространстве изменяются поперечная скорость и магнитная индукция. Покажем, что в случае медленного пространственного изменения магнитного поля, при перемещении заряда абсолютная величина магнитного момента (5.4) сохраняется.

Из курса электродинамики известна сила, действующая в слабо неоднородном маг-

нитном поле на виток с током
r	r		r	(5.5)

F	= grad(µ	const	B) ,

где градиент следует вычислять так, как если бы вектор µ был постоянным. Формула (5.5)

предполагает, что в пределах витка с током индукция магнитного поля почти постоянна. Подставляя в (5.5) выражение (5.4), получим формулу для силы, действующей на заряженную частицу в слабо неоднородном магнитном поле

Fr = −	W	grad \| B \| ,	(5.6)
	\| B \|

где | B | = Bx2 + By2 + Bz2 . Сила (5.6) обусловлена усредненным по ларморовскому вращению

действием на заряд магнитной составляющей силы Лоренца. Видно, что сила (5.6) направле-

на так, что выталкивает частицу из областей сильного поля в области, где поле слабее.

Кинетическая энергия частицы в постоянном магнитном поле сохраняется

Wкин

=W +W||

= const .

(5.7)

Энергия продольного движения W||

в результате работы силы (5.6) изменяется, т.е.

r r

∂ | B |

dW||

= Fdr = −

dr = −

d | B | .

(5.8)

| B |

| B

∂r

Из (5.7) следует соотношение

dW|| = −dW .

(5.9)

Объединяя (5.8) с (5.9), получим равенство

d | B |

(5.10)

| B |

из которого и следует, что

= const .

(5.11)

| B |

Тем самым доказано, что в слабо неоднородном магнитном поле магнитный момент движущегося заряда сохраняет свою величину. Величины, которые сохраняются при медленном изменении условий движения называются адиабатическими инвариантами. Следовательно (5.11) является адиабатическим инвариантом.

Предположим теперь, что магнитное поле изменяется во времени, причем так медленно, что выполнено первое неравенство (5.1). В соответствии с законом электромагнитной

Александров А.Ф., Кузелев М.В. Физика электронных пучков

индукции при этом возникает вихревое электрическое поле, работа которого над электроном приведет к изменению его кинетической энергии. Очевидно, что в итоге работа эта совершается за счет внешнего источника, создающего и изменяющего магнитное поле в системе. Заметим, что при вычислении вихревого электрического поля следует иметь в виду пространственную неоднородность полей. Действительно, из уравнения Максвелла

rotEr = −	1 ∂B	(5.12а)

	c ∂t

следует, что при ∂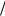∂t ≠ 0 должны отличаться от нуля и какие-то производные E по коорди-

натам. В силу первого неравенства (5.1) выполнено и второе из этих неравенств, а значит в пределах ларморовской окружности заряженной частицы электрическое поле можно считать однородным.

Для вычисления поля E уравнение (5.12а) удобно записать в интегральной форме

r	r	= −	1	∂	r r	(5.12б)
∫Edl			c	∂t	∫∫Bds ,
L					S
где контур		L совпадает с ларморовской орбитой заряда, а				S - поверхность ограниченная

этим контуром. Заметим, что при наличии E ларморовская орбита будет, вообще говоря, незамкнутой, но при выполнении (5.1) этим можно пренебречь. Тогда, из (5.12б) имеем

r	1		d \| B \| r
Е = −		ρe		τ ,	(5.13)
	2c		dt

где τr- единичный вектор касательной к ларморовской орбите, составляющий с B правовин-

товую систему. Легко видеть, что при e > 0 вектор τ	направлен против вращения заряда, а
при e < 0 эти направления совпадают (см. (5.4)), т.е.
−eτrvr =\| ev \|.	(5.14)

Поскольку электрическое поле (5.13) перпендикулярно силовой линии магнитного поля, то составляющая скорости заряда v|| под действием E не меняется. Подставляя (5.13) в

уравнение (1.7), интегрируя это уравнение по периоду циклотронного вращения от t до t +Te и учитывая (5.14), получим следующее соотношение:

mv2		−	mv2		=\| e \| πρ2	1	d \| B \|	.

2	t+T		2	t	e c dt
	e

В соответствии с первым неравенством (5.1) можно записать

mv2			mv2			d mv2
		−			= Te

							2	.
2	t+Te		2	t		dt	2
2	t+Te		2	t		dt

(5.15)

(5.16)

Подставляя (5.16) в (5.15), получим соотношение (5.10), что опять приводит нас к соотношению (5.11). Таким образом, в медленно меняющемся в пространстве и времени магнитном

Александров А.Ф., Кузелев М.В. Физика электронных пучков

поле отношение W 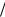| B | является адиабатическим инвариантом.

Из существования адиабатического инварианта можно получить ряд важных следствий. Остановимся на наиболее важном. Из формулы (5.6) следует, что заряженная частица выталкивается в область более слабого магнитного поля. Тем не менее, имея большую и со-

ответствующим образом направленную скорость v|| заряд может двигаться в сторону увели-

чения | B(rr) | . Выясним общий характер этого движения. Исходим из соотношений, являю-

щихся следствием (5.11) и сохранения кинетической энергии

v2 + v||2 = v02 ,

(5.17)

B |

| B |

Здесь

+ v2 - скорость заряда там, где магнитное поле равно

B . Пусть из области,

0||

где поле слабое частица движется в область сильного поля. Из (5.17) имеем

v|| =

v02

− v02 (B2 B02 )= v0 1 − (B2

B02 )sin2 β0 ,

(5.18)

где β

угол между векторами vr

и Br

. По мере продвижения частицы в область сильного

поля продольная скорость уменьшается, и при

B2 =

(5.19)

sin2 β0

продольная скорость обращается в ноль. В точке, где выполнено условие (5.19) заряд отражается и начинает двигаться обратно, в область слабого поля. Это явление имеет место в радиационных поясах Земли – области сильного поля расположены вблизи полюсов, а также используется в магнитных ловушках для удержания плазмы. Слабо неоднородное магнитное поле широко применяется для создания и фокусировки пучков заряженных частиц с задан-

ным отношением v 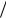v|| . Ниже, во второй главе, будет показано, что фокусирующим дейст-

вием обладает и сильно неоднородное магнитное поле, в котором адиабатическая инвариантность (5.11) не имеет места.

§6. Дрейфовое приближение

Впредыдущем параграфе предполагалось, что в слабо неоднородном магнитном поле движение заряда складывается из вращения по ларморовской орбите и перемещения вдоль силовой линии магнитного поля. На самом деле кроме этих двух основных быстрых движений заряженная частица совершает и медленный дрейф в направлении перпендикулярном к силовым линиям. С дрейфовым движением, обусловленным наличием электрического поля, мы уже имели дело в § 4. Дрейф, связанный с неоднородностью магнитного поля, имеет свои

Александров А.Ф., Кузелев М.В. Физика электронных пучков

отличительные особенности. Дрейфовое движение в неоднородном магнитном поле будет медленным, если неоднородность магнитного поля слабая, т.е. выполнено второе неравенство (5.1). Теория дрейфового движения заряда в неоднородном магнитном поле является приближенной. Она основана на усреднении точных уравнений движения заряженной частицы по быстрому циклотронному вращению.

Представим радиус-вектор заряда в виде

rr(t) = R(t) +ξ (t) ,	(6.1)
где R(t) = {X (t), Y (t), Z(t)}-	радиус-вектор ведущего центра ларморовской орбиты, являю-

щийся медленной функцией времени, а ξ (t) = {ξx (t), ξy (t), ξz (t)}- быстро осциллирующая ве-

личина, описывающая циклотронное вращение вокруг ведущего центра. Подставляя (6.1) в

нерелятивистское уравнение (1.4) (при E = 0

и B , зависящем только от rr) и разлагая с уче-

том (5.1) магнитное поле B(rr) с точностью до линейных по ξ

членов, получим следующее:

(6.2)

+ d

ξ =

+ dξ

dR (ξ )B

dξ (ξ )B

mc dt

Здесь Br0 = Br(Rr) - магнитное поле в точке ведущего центра, а

(ξrr)= ξx ∂∂X +ξy ∂∂Y +ξz ∂∂Z .

В нулевом приближении по неоднородности магнитного поля из (6.2) имеем

d 2 R			e dR		r
		=			B		,
	2
dt				0
			mc dt
d 2ξr			e dξr		r
		=			B0	.
dt	2
			mc dt

(6.3)

(6.4)

Предположим сначала, что движение заряда вдоль силовой магнитного поля отсутствует.

Тогда из первого уравнения (6.4) находим R = R0 = const , а одно интегрирование второго уравнения (6.4) дает (при этом постоянная интегрирования полагается равной нулю, по-

скольку она уже включена в Rr0 )

		dξ	r r
			= ωe[ξ n],				(6.5)
		dt	= ωe[ξ n],				(6.5)
		dt
где	nr- единичный вектор в направлении B			, а	ω	e	- циклотронная частота (3.2). Уравнение
			0			e

первого по неоднородности магнитного поля приближения получается усреднением уравнения (6.2) по быстрому циклотронному вращению, причем, в соответствии с представлением

(6.1) R = R, ξ = 0 , где угловые скобки обозначают усреднение по времени. Усредняя

(6.2), получаем следующее уравнение для радиус-вектора ведущего центра ларморовской орбиты

Александров А.Ф., Кузелев М.В. Физика электронных пучков

rr r

e dR

dξ

(ξ )B

mc dt

Величину

fr = ce ddtξ (ξrr)Br0

(6.6)

(6.7)

можно трактовать как дополнительную среднюю силу, приводящую к дрейфу ведущего центра ларморовской орбиты. Уравнения (6.5) и (6.6) являются основными в теории дрейфового движения заряда в неоднородном магнитном поле.

Выберем локальную систему координат так, чтобы ось z была направлена по магнитному полю Br0 , т.е. Br0 ={0, 0, B0}, nr ={0,0,1} и B0 > 0 . Заметим, что производная n от-

лична от нуля, поскольку направление этого вектора от точки к точке меняется. Тогда из

(6.5) находим (см. (3.8) и (3.9))

ξx = ρe sin ωet, ξy = ρe cosωet, ξz = 0 ,	(6.8)
где ρe = v ωe - ларморовский радиус. Подставляя (6.8) в (6.3) и (6.7), для усредненной силы
получим следующее выражение

mv2

∂B

mv2

= −

grad

B .

(6.9)

2B0

∂X

∂Y

2B0

Здесь i , j - орты локальной системы координат перпендикулярные к силовой линии магнит-

ного поля. Видно, что средняя сила (6.9) пропорциональна второму параметру (5.1), который в дрейфовом приближении мал.

Используя уравнение rotBr0 = 0 , можно записать

		∂B		r		∂B0 y	r	dBr
grad	B =	0 x		i	+		j =	0	.	(6.10)

	0	∂Z				∂Z		dZ

Поясним, что в выбранной при написании (6.9) локальной системе координат в точке R0
имеет место равенство					Br0 = 0 . Однако из-за искривления силовой линии магнитного поля
производная от Br0			по Z , т.е. вдоль силовой линии, в точке R0							отлична от нуля. Пусть при

смещении вдоль силовой линии на dZ единичный вектор n повернулся на угол dα . Оче-

видно, что dBr0 = (B0 dα)sr, где s - единичный вектор, направленный из точки Rr0 в центр

кривизны силовой линии. Обозначим через радиус кривизны силовой линии в точке R0 .

По определению dα = dl ≈ dZ , где dl - элемент длины дуги силовой линии. С учетом сказанного (6.10) преобразуем к виду

grad	B	=	B0	sr .	(6.11)

	0

<<< < Предыдущая 12 / 292 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке ЭЛТ

#
29.03.20164.53 Mб3427_VaN[1].pdf
#
29.03.2016116.12 Кб20Мониторы с ЭЛТ лекция.mht
#
29.03.20166.45 Кб22Схема монитора с ЭЛТ.gif
#
29.03.201634.05 Кб21Устройство кинескопа.jpg
#
29.03.2016133.55 Кб21Устройство монитора на ЭЛТ.jpg
#
29.03.201622.05 Кб22Устройство ЭЛТ.gif