ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]

Здесь, чтобы не возникло путаницы, индекс суммирования по компонентам плазмы обозначен через µ . Уравнений (21.11) столько, сколько имеется сортов частиц α . Неизвестных же функций Nα (r) , βαϕ и βαz , которые подлежат определению, в три раза больше. Поэтому за-

дача равновесия рассматриваемой заряженной плазмы имеет не единственное решение. Мы, исходя из разумных физических соображений, будем задавать некоторые из неизвестных функций, а остальные определим из уравнений баланса радиальных сил (21.11).

§ 22. Нерелятивистское недиамагнитное равновесие

Аксиальное собственное магнитное поле электронного пучка Bz , обусловленное его азимутальным вращением во внешнем магнитном поле B0 , направлено навстречу внешнему магнитному полю. То есть электронный пучок, подобно диамагнетику, стремится ослабить внешнее магнитное поле. Если этот эффект незначителен, то можно ограничиться недиамагнитным приближением. Используя вторую формулу (21.6) и учитывая, что собственное аксиальное магнитное поле максимально на оси симметрии r = 0 , условие пренебрежения диамагнетизмом пучка запишем в виде

Считаем, что неравенства (22.1) и (22.2) удовлетворяются и для всех других сортов частиц плазмы (для сортов частиц, используем обозначения: α = b - электроны пучка; α = e - электроны плазмы; α = i - ионы).

В условиях (22.1) и (22.2) уравнение баланса (21.11) записывается в виде

перепишем уравнение (22.3) следующим образом (для частиц каждого сорта):

91

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Если известны угловые скорости вращения ωα (r) , то из (22.5) следует система уравнений для определения профилей поперечного распределения компонент плазмы Nα (r) :

В дальнейшем подход, основанный на уравнениях (22.8), мы использовать не будем.

Из (22.7) следует условие, необходимое для того, чтобы у рассматриваемой плазмы имелось стационарное состояние. А именно: для всех сортов частиц α должно быть

Ограничение, накладываемое неравенством (22.9) означает, что в любой точке плазмы силы магнитного сжатия превосходят силы электростатического расталкивания и, следовательно, выполняется условие радиального удержания всех компонент в равновесии.

В качестве примера рассмотрим плазму с равномерным распределением плотности каждой компоненты по поперечному сечению, т.е.

Если плазма состоит из двух компонент – электроны пучка с плотностью n0b и бесконечно тяжелые водородоподобные ионы с плотностью n0i = f n0b и массой mi → ∞ , то формула

(22.11) для электронов дает результат (20.9), а угловая скорость ионов равна нулю. Учет ко-

нечности массы ионов mi приводит к не нулевому значению для их угловой скорости, а уг-

92

Александров А.Ф., Кузелев М.В. Физика электронных пучков

ловая скорость электронов пучка дается той же формулой, а именно:

(ωLi2 = 4πe2n0i 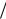mi ). Мы видим, что угловые скорости вращения электронной и ионной компо-

нент различны. В дальнейшем (см. § 38) будет показано, что наличие относительного движения электронов и ионов может быть причиной развития в системе неустойчивости.

Из формулы (22.11) следует, что в случае распределения плотностей (22.10) угловые частоты вращения не зависят от координаты r , т.е каждая компонента плазмы вращается как твердое тело – так называемый жесткий ротатор. При этом говорят, что «шир» угловой скорости внутри каждой компоненты отсутствует. Рассмотрим пример с наличием шира угловой скорости. Пусть распределение плотности имеет вид

Из (22.14) видно, что угловая скорость зависит от r , т.е. имеется шир угловых скоростей вращения. Можно показать, что этот шир приводит к возникновению так называемой slip- ping-неустойчивости.

Придадим еще явный вид неравенству (22.1), обеспечивающему малость диамагнетизма электронов пучка. В отсутствии шира скоростей и с учетом (22.4) неравенство (22.1) записывается в виде

где ωb(±) - одна из величин (22.12). Поскольку максимальное значение угловой скорости есть

ωb(+) и ωb(+) < Ωe , то неравенство (22.15) можно переписать следующим образом:

С другой стороны, поскольку ωb(+)r0 есть максимальное значение азимутальной скорости электронов пучка, то условие (22.15) согласуется со вторым неравенством (22.2).

93

Александров А.Ф., Кузелев М.В. Физика электронных пучков

§ 23. Равновесие релятивистского электронного пучка

Применим теперь уравнение (21.11) баланса радиальных сил для исследования равновесия релятивистского электронного пучка, распространяющегося параллельно внешнему магнитному полю Br = {0,0, B0 }. При этом пока не будем пренебрегать диамагнитным эффек-

том. Движение тяжелых ионов, частично нейтрализующих объемный заряд пучка, для простоты не учитываем. Предположим также, что гидродинамические плотности электронов пучка и неподвижных ионов связаны локальным соотношением

Ni (r) = f Nb (r) , (23.1)

а частиц других сортов нет. Кроме того, потребуем, чтобы распределение аксиальной скорости электронов пучка в поперечном сечении было равномерным, т.е.

Уравнение баланса (21.11) для электронов пучка, с учетом (23.1), (23.2) и определения (22.4), записывается в виде

ском случае (формально при с → ∞ ) уравнение (23.3) переходит в (22.5).

Перечислим физический смысл каждого из членов в уравнении баланса (23.3). Первое слагаемое обусловлено “растаскивающим” действием центробежной силы; слагаемое, пропорциональное (1 − f ) , обязано существованием расталкивающей электростатической силе;

член, пропорциональный − β02 , обусловлен силой магнитного сжатия, действующей со сто-

роны собственного азимутального магнитного поля Bϕ (r) ; слагаемое с множителем c−2 опи-

сывает диамагнитные свойства электронного пучка и приводит к его расталкиванию; наконец, последнее слагаемое обусловлено сжимающим (точнее удерживающим) действием со стороны внешнего магнитного поля.

Выясним, существует ли равновесное состояние электронного пучка, когда у него полностью отсутствует вращательное движение, т.е.

Вэтом случае уравнению баланса (23.3) удовлетворяет любое распределение плотности

ωLb2 (r) электронов пучка и при любом внешнем магнитном поле Ωe , но только если выпол-

нено условие

94

Условие (23.5) отражает точный баланс сил электростатического расталкивания и магнитного сжатия собственным азимутальным магнитным полем.

Предположим теперь, что вращательное движение пучка есть, но является нерелятивистским, т.е.

При этом можно пренебречь диамагнитным эффектом и записать уравнение (23.3) в виде

Из (23.8) следует, что при выполнении условия

β02 ≥1 − f (23.9)

равновесие пучка возможно и без внешнего магнитного поля. Считая (23.9) выполненным и полагая в (23.8) Ωe = 0 , для частот вращения имеем

Равновесие в отсутствии внешнего магнитного поля поддерживается азимутальным собст-

венным магнитным полем пучка Bϕ (r) , создаваемым продольным током пучка. Сам пучок при этом вращается с частотой (23.10). То есть, при Ωe = 0 и β02 >1− f для баланса ради-

альных сил необходима центробежная сила, обусловленная вращением. Если вращения нет,

или оно не достаточно, то собственное поле Bϕ сжимает пучок, при этом уменьшается ко-

эффициент его зарядовой нейтрализации f (ионы неподвижны), а значит увеличивается электростатическое расталкивание пучка, пропорциональное 1 - f. Сжатие продолжается до тех пор, пока не установится баланс трех сил – магнитной, электростатической и центробежной.

В случае распределения плотности пучка вида (22.10)

из общей формулы (23.8) имеем:

95

Александров А.Ф., Кузелев М.В. Физика электронных пучков

В нерелятивистском случае ( β02 <<1, γ0 ≈1) выражения (23.12) переходят в первую формулу

(22.12). Для распределения вида (22.13)

Как и в нерелятивистском случае (см. (22.14)) в полом пучке с трубчатым распределением плотности имеется шир угловой скорости.

Из (23.12) имеем неравенство

необходимое для существования у пучка с распределением плотности вида (22.10) стационарного состояния (см. также (22.9)). В случае трубчатого пучка, с распределением плотности вида (22.13), условие существования стационарного состояния имеет вид

В дальнейшем (см. § 26) будет показано, что даже в случае не нейтрализованного пучка

( f = 0 ) и при большом его релятивизме (γ0 >>1), условие (23.17) выполняется уже при не очень сильном внешнем магнитном поле.

§ 24. Учет диамагнетизма пучка и релятивизма вращательного движения

Отказ от предположения (23.6) значительно усложняет исследование равновесных конфигураций пучка. Основные трудности связаны как с учетом диамагнитных эффектов,

так и с зависимостью релятивистского фактора пучка γb (r) от угловой скорости (см. (21.9)).

Эти трудности, по крайней мере на качественном уровне, можно обойти в важном случае

96

Александров А.Ф., Кузелев М.В. Физика электронных пучков

тонкого (точнее бесконечно тонкого) трубчатого пучка, рассмотрением которого, не предполагая выполненным неравенство (23.6), мы здесь и ограничимся. Плотность электронов такого пучка определяется формулой

(24.1) уравнение (23.3) имеет смысл только в одной точке r = rb , хотя формально этим урав-

нением можно пользоваться и при тех r , где плотность пучка равна нулю. Запишем уравнение (23.3) баланса радиальных сил в следующем виде:

образного распределения плотности заряда (24.1). Будем использовать следующее естест-

венное обобщение основного свойства δ - функции - ∫ f (x)δ(x)dx = f (0) , а именно:

Используя (24.5), в результате выполнения интегрирования в (24.4) получим следующее уравнение для частоты вращения тонкого трубчатого пучка ω = ωb (rb ) :

97

Александров А.Ф., Кузелев М.В. Физика электронных пучков

нечно тонкого трубчатого пучка. Однако, вопрос этот важный, поскольку при переходе от интегрального уравнения (24.2) к локальному уравнению (24.4) требовалось вычислить интегралы

∫ωb (r)δ(r − rb )dr,

(24.7)

∫γb (r)ωb2 (r)δ(r − rb )dr.

Для исследования структуры функции ωb (r) и снятия вопросов, связанных с ее разрывом,

используем вместо (24.1) иное распределение плотности электронов пучка. А именно:

где ε << rb . В пределе ε → 0 распределение (24.8) переходит в (24.1). Заметим, что по смыс-

лу величины ∆b и 2ε эквивалентны. Однако, при совершении предельного перехода ε → 0

погонную плотность пучка n0b∆b следует считать постоянной. Интегралы (24.7) должны вы-

числяться на сегменте r [rb −ε, rb + ε] .

Согласно формуле (23.14), не учитывающей диамагнетизм и релятивизм вращения, для распределения (24.2) имеем следующее выражение для угловой скорости пучка:

При наличии диамагнетизма пучка и релятивизма его вращения формула (24.10) конечно не верна. В этом случае для определения ω должно использоваться уравнение (24.6). Таким образом, ω в уравнении (24.6) есть угловая скорость некоторой внутренней точки пучка – угловая скорость, усредненная по ширу вращения.

Перейдем теперь к исследованию уравнения (24.6). Основная трудность при этом связана с нелинейным вхождением ω в релятивистский фактор γ , т.е. с релятивизмом враща-

тельного движения. Диамагнетизм же приводит к элементарной поправке – второму слагае-

мому в коэффициенте при ω2 . В общем случае уравнение (24.6) решается только численно. При численном решении удобно использовать безразмерные величины

98

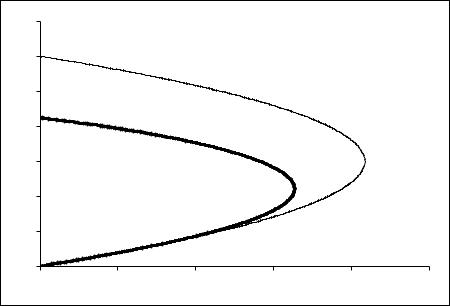
Рассмотрим результаты численного решения уравнения (24.12). Ограничимся случаем полностью не нейтрализованного электронного пучка, т.е. f = 0 . На Рис. 24.1 показаны безраз-

мерные угловые скорости y(x) , вычисленные при β0 = 0,8 и z =1. Кривая 1 получена из уравнения (24.12), а кривая 2 найдена из уравнения, в котором не учтены релятивизм вращательного движения и диамагнетизм, т.е. из уравнения (23.7), которое в переменных (24.11) имеет вид

Из Рис. 24.1 следует, что релятивизм вращательного движения пучка существенно уменьша-

ет высокую частоту ω(+) . Кроме того, уменьшается область (по безразмерной плотности x )

существования стационарного состояния пучка. Первое обстоятельство связано, в основном, с релятивизмом вращения, а второе – с диамагнетизмом пучка. На Рис. 24.2 для z =1 и раз-

личных β0 (значения указаны рядом с кривыми y(x) ) представлены безразмерные угловые скорости y(x) . Видно: чем больше продольная скорость, тем ниже обе частоты вращения

ω(±) . На Рис. 24.3 изображено то же, что и на предыдущем рисунке, но при большем магнит-

ном поле - z = 5 . Зависимости ω(+) и ω(−) стали асимметричны относительно их полусуммы.

Угловая скорость ω(+) слабее зависит от плотности пучка, чем скорость ω(−) . Асимметрия возрастает с увеличением внешнего магнитного поля и уменьшением продольного релятивизма (Рис. 24.4). На Рис. 24.5 показаны максимальные значения безразмерной плотности электронов пучка xmax как функции безразмерного магнитного поля z , рассчитанные при различных значениях β0 . При x > xmax стационарных состояний рассматриваемого вида у тонкого трубчатого пучка нет. Результат оказывается вполне очевидным: чем выше внешнее магнитное поле и больше продольный релятивизм пучка, тем шире область существования стационарных состояний. Заметим, что это не противоречит данным Рис. 24.1. Кривая 2 на этом рисунке получена из не применимого для взятых параметров уравнения (24.13). Напротив, Рис. 24.5 (также как и Рис. 24.2-24.4) построен по результатам решения верного уравне-

ния (24.12).

Рассмотрим теперь некоторые результаты аналитического анализа уравнений (24.6) и (24.12), которые приведем здесь только для частного случая f = 0 . Граница области сущест-

99

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.1

Безразмерные угловые скорости вращения y = ωrb 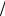c тонкого трубчатого пучка во внешнем магнитном поле при z = Ωerb c =1 и β0 = 0,8 :

1 – с учетом диамагнетизма и релятивизма вращения;

2 – без учета диамагнетизма и релятивизма вращения

100