ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]

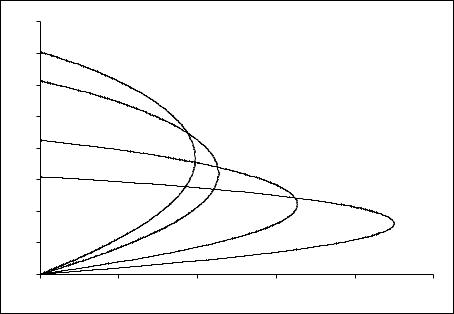
Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.2

Безразмерные угловые скорости вращения y = ωrb c тонкого трубчатого пучка во внешнем магнитном поле при z = Ωerb c =1 и различных β0 : 0,1; 0,5; 0,8; 0,9

101

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.3

Безразмерные угловые скорости вращения y = ωrb c тонкого трубчатого пучка во внешнем магнитном поле при z = Ωerb 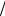c = 5 и различных β0 : 0,1; 0,5; 0,8; 0,9

102

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.4

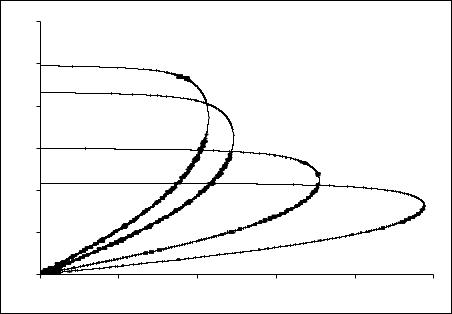
Безразмерные угловые скорости вращения y = ωrb 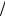c тонкого трубчатого пучка во внешнем магнитном поле при z = Ωerb 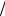c =10 и различных β0 : 0,1; 0,5; 0,8; 0,9

103

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.5

Максимальная безразмерная плотность пучка x = ∆brbωLb2 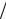2c2 в зависимости от безразмерного внешнего магнитного поля z = Ωerb 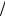c при различных β0 : 0,1; 0,5; 0,8; 0,9

104

Александров А.Ф., Кузелев М.В. Физика электронных пучков

вования стационарных состояний пучка приближенно определяется соотношениями

удовлетворительно согласующимися с данными Рис. 24.5. При x << xmax из (24.12) имеем два выражения для безразмерных угловых скоростей вращения пучка

Всегда y(+) ≥ y(−) (равенство достигается только при x = xmax , когда формулы (24.15) не при-

менимы), причем максимум y(+) достигается при x = 0 . Поэтому величина y(+) из (24.15)

дает максимальное значение безразмерной угловой скорости трубчатого пучка. С другой сто-

роны, вращательное движение пучка является нерелятивистским, если y2 <<1 − β02 (см. (23.6)). Отсюда, с учетом (24.15), устанавливаем, что релятивизм вращательного движения пучка несущественен, если выполнено неравенство

Однако, условие (24.16) касается только вращения пучка с высокой угловой скоростью y(+) .

Вращение же с низкой скоростью y(−) при x << xmax , как это следует из (24.15), является всегда нерелятивистским.

В размерном виде угловые скорости (24.15) определяются формулами

Из (24.17) следует, что при слабом внешнем магнитном поле ( z <<1), когда вращательное движение пучка нерелятивистское , угловая скорость ω(+) совпадает с релятивистской цик-

лотронной частотой Ωe 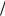γ0 , причем релятивизм здесь обусловлен только аксиальным движе-

нием электронов. В сильном магнитном поле, z >>1, когда вращение является релятивист-

ским, скорость ω(+) оказывается качественно иной. Её можно получить, если полный реля-

тивистский фактор электрона γb = (1− β02 − y2 )−12 приравнять к бесконечности, т.е. более вы-

сокой угловой скорости вращения пучка, чем c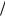rbγ0 , в принципе быть не может. Угловая

105

Александров А.Ф., Кузелев М.В. Физика электронных пучков

скорость ω(−) качественно (т.е. по структуре и физическому смыслу) не отличается от скоро-

сти ωb(−) в формулах (20.11). Вообще, релятивистские эффекты при вращении пучка со скоро-

стью ω(−) несущественны, пока x << xmax .

Определим теперь, когда существенны, или не существенны диамагнитные эффекты. Из уравнения (24.6) следует, что диамагнетизм электронного пучка мал при x << γ . Отсюда

находим условие, когда диамагнитными эффектами можно пренебречь,

Неравенство (24.18) согласуется с условием (22.16), полученным для случая нерелятивистского сплошного пучка. Неравенство (24.18) не сложно получить и из общего условия (22.1) с учетом (24.15). Из (24.18) и (24.14) следует, что при z <<1 диамагнитные эффекты всегда малы, а при z >>1 в случае пучков большой плотности учитывать их необходимо. При вра-

щении пучка на скорости ω(−) , пока x << xmax , диамагнитные эффекты несущественны.

При z <<1 и x << γ0 , когда вращательное движение нерелятивистское и диамагнит-

ные эффекты несущественны, для угловых скоростей из (24.6) имеем, как это и должно быть, выражения (24.10). Эти выражения, хотя и согласуются с формулами (23.14), но все же от них отличаются качественно: формулы (23.14) описывают шир угловой скорости, а формулы (24.10) получены усреднением по ширу вращения.

При больших z и произвольных x уравнение (24.12) аналитически исследовать достаточно сложно. Поскольку случай сильного внешнего магнитного поля представляет значительный интерес, снова обратимся к результатам численных расчетов. На Рис. 24.6 для раз-

дует, что в случае сильного внешнего магнитного поля угловые скорости пучка приближенно определяются выражениями

т.е. формулы (24.15) и (24.17) при z >>1 приближенно работают и при достаточно больших x , но тем хуже, чем x ближе к xmax .

В связи с формулами (24.19) обсудим вопрос о возможной реализации исследованных равновесных состояний пучка. Выражая y через γ и γ0 , имеем соотношение

106

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 24.6

Безразмерные угловые скорости вращения y = ωrb 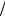c тонкого трубчатого пучка при β0 = 0,9 в сильных внешних магнитных полях z = Ωe rb 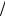c : 5; 10; 50; 100

107

Полный релятивистский фактор пучка γ следует считать величиной заданной, определяемой ускоряющим напряжением сильноточного диода. Продольный релятивистский фактор γ0

может изменяться от единицы до γ : при γ0 =1 все движение пучка связано с его вращением,

при γ0 = γ вращения у пучка вообще нет.

Если подставить в (24.20) y = y(+) , где y(+) определен в (24.19), то получим, что должно быть γ >>1 (точнее γ → ∞). Следовательно, равновесное вращение трубчатого пуч-

ка в сильном магнитном поле на высокой частоте ω(+) возможно только при большой энер-

которое, как следует из Рис. 24.5, при z >1 легко может быть выполнено при некотором

x < xmax .

§ 25. Пинч Беннета

Для того чтобы построить модель пинча Беннета в уравнение баланса радиальных сил следует ввести силу, обусловленную давлением электронного газа. Как следует из уравнения (18.2), эта сила определяется тензором давления, который через гидродинамические величины нами выражен не был. В модели пинча Беннета принимается, что внешнее магнитное поле и вращение пучка вокруг оси симметрии отсутствуют. В этих условиях, когда анизотропия системы обусловлена только направленным движением электронов пучка, естественно считать давление не тензорной величиной, а скалярной. Тогда радиальная сила давления

Давление стационарного электронного газа вычисляется по изотермическому уравнению состояния

где Tb = const - температура, κ - постоянная Больцмана.

Будем считать, что электронный пучок не вращается и его аксиальная скорость постоянна в поперечном сечении, т.е.

108

Александров А.Ф., Кузелев М.В. Физика электронных пучков

означающее, что силы магнитного сжатия собственным полем Bϕ (пинч-эффект) достаточ-

ны, чтобы скомпенсировать электростатическое расталкивание и газодинамическое расширение. Решение уравнения (25.5) записывается в виде

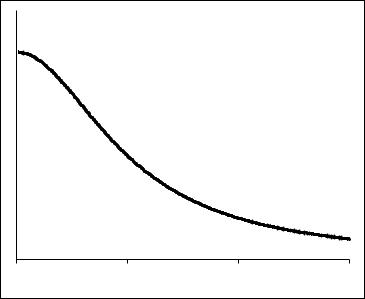
а rD = κTb mωLb2 (0) - дебаевский радиус электрона на оси электронного пучка. На Рис. 25.1

показано определяемое формулой (25.7) колоколообразное распределение электронов по поперечному сечению пинча Беннета.

109

Александров А.Ф., Кузелев М.В. Физика электронных пучков

N b

r/a

Рис. 25.1

Профиль плотности электронов в пинче Беннета

110