ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]

Александров А.Ф., Кузелев М.В. Физика электронных пучков

где Gn = Sb ϕn −2ϕn2 (rrb ) - геометрический фактор тонкого пучка в однородном плазменном волноводе. В случае цилиндрической геометрии (см. Рис. 16.2) для геометрического фактора имеем

Поэтому, с учетом данной замены, все результаты анализа уравнения (37.3) сохраняются и при резонансной неустойчивости тонкого электронного пучка в плазменном волноводе.

Нелинейное рассмотрение проведем только для случая резонансной неустойчивости тонкого электронного пучка малой плотности в волноводе со сплошным однородным плазменным заполнением. Учитывая, что при резонансной неустойчивости искажение поперечной структуры поля плазменной волны мало и вклад высших продольных пространственных

которые являются аналогами неравенств (32.8) и (37.8) соответственно. Подставим далее (37.18) в уравнения (37.1), вычислим ток пучка через интеграл по начальным данным, учтем неравенства (37.19) и перейдем к безразмерным переменным (см. (35.4)). В результате полу-

δω - инкремент резонансной неустойчивости тонкого пучка в плазменном волноводе. Он, как следует из анализа уравнения (37.16), дается формулой (37.9) с заменой ωLb2 →GnωLb2 . Таким образом, нелинейная теория резонансной пучковой неустойчивости в плазменном волноводе в целом сводится к изложенному ранее в § 35. Но это не совсем так: в силу неравенства (37.8) при неустойчивости в волноводе уравнения (35.7) применимы только, если µ <<1. С

ростом параметра µ , особенно при нарушении неравенства (37.14), проявляются особенно-

сти, связанные с непотенциальностью плазменных колебаний в волноводе. Это приводит к тому, что эффективность пучково-плазменного взаимодействия при резонансной неустойчивости в волноводе спадает при µ >1 быстрее, чем показано на Рис. 35.6.

181

Александров А.Ф., Кузелев М.В. Физика электронных пучков

§ 38. Неустойчивость плазмы с током

Рассмотрим одномерные электростатические колебания в холодной однородной безграничной плазме, в которой электроны движутся относительно ионов с нерелятивистской скоростью ur = {0,0,u}. Исходим из следующих линейных уравнений, являющихся аналогом уравнений (32.1) и (32.2) пучковой неустойчивости в безграничной плазме:

Здесь ji,e и ρi,e - плотности тока и заряда ионной и электронной компонент плазмы, а ωLi и

ωLe - ленгмюровские частоты ионов и электронов соответственно. Считаем ионы однозаряд-

ными, поэтому ωLi2 = (m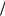M )ωLe2 , где M - масса иона.

Представляя возмущенные величины в виде ~ exp(−iωt +ikz z) , получим из уравнений

(38.1) следующее дисперсионное уравнение:

Левая часть соотношения (38.2) есть продольная диэлектрическая проницаемость холодной электронно-ионной плазмы с током. При анализе уравнения (38.2) следует учитывать, что имеет место неравенство

На Рис. 38.1 показан качественный ход дисперсионных кривых уравнения (38.2), построенных для отношения α = ωLi ωLe = 0,0234 , что соответствует водородной плазме. Дан-

ный рисунок целесообразно сопоставить с Рис. 32.1. Поскольку ωLe2 >> ωLi2 , вклад ионов в дисперсионное уравнение может быть заметным только в области малых частот

182

Александров А.Ф., Кузелев М.В. Физика электронных пучков

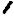y

x

Рис. 38.1

Дисперсионные кривые уравнения (38.2) при α = 0,02 . x = ku ωe , y = ω ωe

183

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Отсюда находим выражения для частот колебаний

Из (38.6) следует, что при | kzu | < ωLe плазма с током неустойчива. Это видно и из Рис. 38.1.

Данная неустойчивость называется нерезонансной неустойчивостью Бунемана.

Для выяснения физического механизма нерезонансной неустойчивости учтем, что отклик движущихся электронов на низкочастотное внешнее воздействие определяется их продольной диэлектрической проницаемостью

тельна. Таким образом, нерезонансная неустойчивостью Бунемана обусловлена отрицательностью квазистатической диэлектрической проницаемости (38.7): соотношение (38.8) следует рассматривать как дисперсионное уравнение ионных ленгмюровских волн в среде с про-

ницаемостью εe . Нерезонансная неустойчивость Бунемана вполне аналогична апериодиче-

ской пучковой неустойчивости в плазме, т.е. она принадлежит к неустойчивостям типа отрицательной массы. Нерезонансная бунемановская неустойчивость приводит к спонтанной самомодуляции ионного фона в плазме.

При | kzu | = ωLe формулы (38.6) не применимы. Для анализа этого случая перепишем

найдем следующие выражения для комплексных частот:

Заметим, что если условие резонанса взять в виде kzu = −ωLe , то для частот получатся не-

сколько иные формулы

184

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Неустойчивость с инкрементом (38.11) называется резонансной неустойчивостью Бунемана. Эта неустойчивость имеет максимальный инкремент. Легко видеть, что неравенства (38.10) сводятся к условию (38.3). В дальнейшем, в § 39, мы уточним физический механизм резонансной неустойчивости Бунемана и определим ее место в ряду других резонансных неустойчивостей прямолинейных электронных пучков (потоков) в плазме.

Перейдем теперь к нелинейной теории. Ограничимся рассмотрением только резонансной неустойчивости Бунемана, поскольку она имеет максимальный инкремент. Возможны два механизма насыщения этой неустойчивости. Из (38.11) следует, что

т.е. возбуждаемая при неустойчивости волна распространяется в ту же сторону, что и электроны плазмы. В принципе эта волна может дорасти до такого уровня, что захватит ионы и будет их ускорять. Но возможно, что данная волна раньше захватит электроны. Причем, поскольку фазовая скорость (38.12) много меньше невозмущенной скорости электронов u , захват электронов приведет к полному срыву тока в плазме. Легко показать, что имеет место именно второй механизм насыщения. Действительно, захват ионов невозможен, если

где E0 - амплитуда электрического поля волны. Оценивая E0 из условия полной модуляции электронной компоненты плазмы по плотности, получаем, что неравенство (38.13) сводится к условию (ωLi2 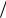ωLe2 )13 <<1 , которое, очевидно, имеет место. Выполнение сильного неравен-

ства (38.13) позволяет при исследовании нелинейной динамики резонансной бунемановской неустойчивости движение ионов описывать в линейном приближении.

Исходим из следующих нелинейных уравнений потенциального приближения, являющихся аналогом уравнений (34.1) нелинейного пучково-плазменного взаимодействия:

Начальные условия для уравнений (38.14) имеют вид

185

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Подставляя в (38.14) электрическое поле в виде разложения (34.4), получим следующие уравнения, описывающие нелинейную динамику неустойчивости Бунемана:

вочную) модуляцию электронной компоненты плазмы по плотности. Кроме того, при резонансной неустойчивости в (38.16) следует положить ϑ =1.

При выполнении сильного неравенства (38.13) уравнения движения ионов можно линеаризовать, что дает

Система уравнений (38.16) справедлива в любом случае. Если же для описания ионной ком-

поненты вместо уравнения для yi используются уравнения (38.18), то соответствующая сис-

тема уравнений будет верна только в случае резонансной неустойчивости Бунемана. Важной характеристикой рассматриваемой неустойчивости является постоянная со-

ставляющая электронного тока в плазме, определяемая в безразмерной форме выражением

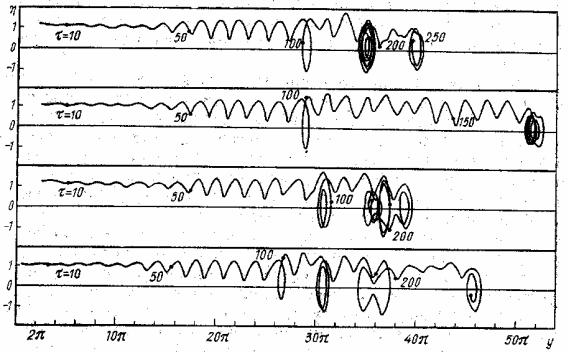
Величина (38.19) зависит от времени, но не от пространственной координаты z . Рассмотрим результаты численного моделирования резонансной (ϑ =1) неустойчиво-

сти Бунемана в водородной плазме ( m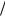M = 5,45 10−4 ). В такой плазме обратный безразмер-

ный инкремент τ0 ≈18 . Положим α~ = 0.01, что означает начальную модуляцию плотности электронов на уровне 1%. На Рис. 38.2 изображены как функции безразмерного времени τ амплитуды первой и второй гармоник плотности электронов | ρe1 | и | ρe2 | , а также постоян-

ная составляющая электронного тока (38.19). Видно, что нелинейное насыщение роста ам-

186

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 38.2

Динамика амплитуд гармоник плотности электронов и постоянной составляющей тока при резонансной неустойчивости Бунемана

187

Александров А.Ф., Кузелев М.В. Физика электронных пучков

плитуд гармоник плотности электронов происходит за время трех-четырех обратных инкрементов неустойчивости (τ ≈ 60 ). На более поздней стадии (τ ≈100 ) происходит полный

срыв электронного тока в плазме, что обусловлено захватом электронов полем Ez , которое медленно меняется со временем и имеет пространственный период u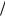ωe . На Рис. 38.3 пред-

ставлены фазовые траектории некоторых электронов плазмы: в результате захвата электрическим полем электроны останавливаются, что и приводит к срыву тока.

Сильное изменение постоянной составляющей тока в плазме при неустойчивости Бунемана приводит к необходимости учитывать факторы, поддерживающие ток, например, индуктивность системы(*). Для этого к электрическому полю (34.4) следует добавить постоян-

ную составляющую E0 (t) . В рамках первого уравнения системы (38.14) постоянную состав-

ляющую электрического поля описать нельзя, поскольку возникновение её обусловлено ис-

По поводу уравнения (38.20) требуются разъяснения. Во-первых, в правой части этого уравнения содержится только возмущение постоянной составляющей полного тока, т.е. в по-

тенциал A0 не входит вклад от статического магнитного поля тока в плазме в невозмущен-

ном состоянии. Следовательно, при t = 0 имеем A0 = 0 . Во-вторых, предполагается зависи-

мость векторного потенциала от поперечной к направлению тока координаты rr , без чего корректное вычисление постоянной составляющей E0 (t) невозможно. Что касается пере-

менных (зависящих от z ) составляющих поля (34.4), то при неустойчивости Бунемана их можно вычислять в потенциальном квазиодномерном приближении, хотя учесть реальную зависимость величин E n от rr не представляет труда. С той же точностью оператор ∆ в

уравнении (38.20) можно заменить на ( − k 2 ), где k ~ R−1 , а R - поперечный размер плазмы с током. Добавляя в правые части уравнений (38.16) вклады от постоянной составляющей электрического поля и переходя в (38.20) к безразмерным переменным, запишем следующую систему уравнений для координат электронов и ионов плазмы и уравнение для безразмерной постоянной составляющей электрического поля:

(*) В случае пучково-плазменной неустойчивости изменение постоянной составляющей полного тока мало, (см. неравенство (34.13)), а в потенциальном приближении оно вообще отсутствует.

188

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Рис. 38.3

Некоторые характерные фазовые траектории электронов плазмы при резонансной неустойчивости плазмы

189

Здесь

постоянная составляющая плотности полного тока в плазме, отнесенная к плотности тока в невозмущенном состоянии (ионный вклад в (38.22) мал, поэтому вполне можно использовать

параметр, от величины которого, как будет показано ниже, существенно зависит динамика постоянной составляющей тока в плазме.

Уравнение для постоянной составляющей тока получается из первых двух уравнений системы (38.21)

Без учета же постоянной составляющей электрического поля то же самое уравнение, как это следует из (38.16), имеет вид

используя которое перепишем уравнение (38.25) в виде

190