
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|||||
|
|
L |
|
π U |
|
|||
ω = iaLδ = ia |
|
|
a − |
. |
(47.7) |
|||
U |
||||||||
|
|
|
2 L |
|
||||
В общем случае даже простейшее уравнение (47.2) решается только численно. Введем |
||||||||
безразмерные частоту x и параметр плотности пучка σ |
|
|||||||
x = ω , |
σ = 2a |
L |
. |
|
(47.8) |
|||
|
|
|||||||
a |
|
|
|
U |
|
|
||
В новых переменных уравнение (47.2) запишется в виде |
|
|||||||
exp(iσ |
1+ x2 )= x + |
1+ x2 . |
(47.9) |
|||||
|
|
|
|
x − |
1+ x2 |
|
||
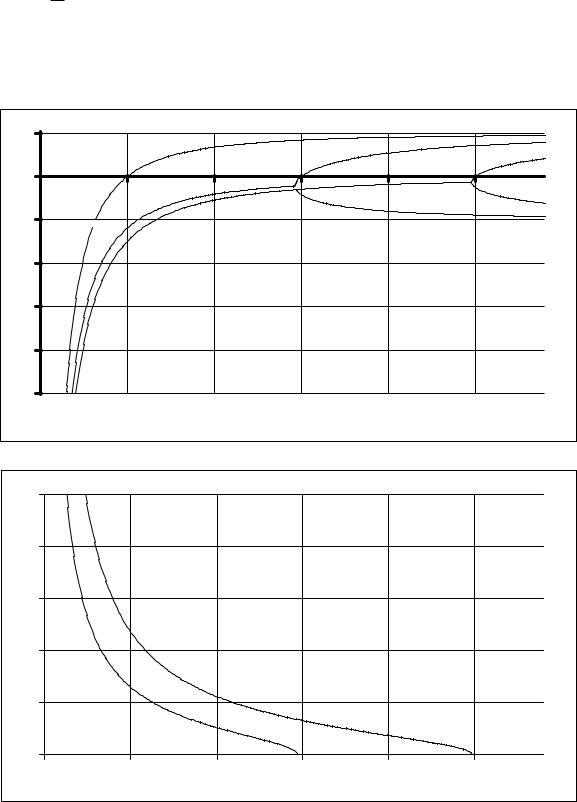
На Рис. 47.1 представлены зависимости безразмерных частот x = Re x + i Im x |
от па- |
|||||||
раметра плотности пучка σ , полученные из уравнения (47.9) численно. Имеется бесконечное множество продольных мод колебаний (на рисунке показаны частоты продольных мод с n = 0, 1, 2 ). Пороги развития неустойчивости для каждой из мод, как показано в (47.3), равны
σ =π (2n +1) . Частота моды n = 0 является чисто мнимой: при изменении σ от 0 до ∞ мнимая частота Im x этой моды изменяется от − ∞ до 1. Остальные моды n =1, 2,K на на-
чальном участке изменения σ также имеют растущую Im x , а кроме того не равные нулю и противоположные по знаку действительные части частот ± Re x (на Рис. 47.1 показаны толь-
ко Re x ≥ 0 ). У порога неустойчивости мод с n =1, 2,K действительные части Re x обраща-
ются в нуль. При дальнейшем увеличении σ у этих мод обе действительные части Re x ≡ 0 ,
но имеются две различные мнимые части Im x : растущая к +1 и убывающая к −1.
В переменных (47.8) решение (47.5) дается формулой
x = i |
2 |
|
1+ |
π |
|
(47.10) |
|
|
|
(σ −π) −1 . |
|||
|
π |
|
|
2 |
|
|
|
|
|
|
|
На Рис. 47.2 представлен результат сравнения (около порога неустойчивости) аналитического решения (47.10) – сплошная линия, с численным решением уравнения (47.9) – пунктирная линия. Наблюдается хорошее совпадение результатов.
Обсудим физический смысл порогового условия (47.6). Коллективный эффект Черенкова на встречной волне является абсолютной неустойчивостью, при которой возмущения неограниченно нарастают в любой точке пространства. При Vg < 0 и |Vg |=U собственные частоты, определяемые из первого дисперсионного уравнения (46.1), даются формулами:
ω = ± k 2U 2 − a2 . (47.11)
Следовательно, неустойчивость имеется только в следующей области волновых чисел
231
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
||||
| k |< |
a . |
|
|
|
(47.12) |
|
U |
|
|
|
|
В системе протяженностью L длина волны возмущений не может превосходить значения |
|||||
1 |
Im x |
0 |
|
|
|
|
|
1 |
2 |
||
0 |
|
|
|||
|
|
|
|
σ |
|
-1 |
|
|
|
|
|
-2 |
|
|
|
|
|
-3 |
|
|
|
|
|
-4 |
|
|
|
|
|
-5 |
|
|
|
|
|
0 |
3.14 |
6.28 |
9.42 |
12.56 |
15.7 |
10 |
Re x |
|
|
|
|
|
|
|
|
|
|
8
6 |
|
|
|
|
|
4 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
σ |
0 |
3.14 |
6.28 |
9.42 |
12.56 |
15.7 |
Рис. 47.1
Зависимости безразмерной частоты x от параметра плотности пучка σ при коллективном эффекте Черенкова на встречной волне
в резонаторе без отражений, к = 0
232

Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
Im x |
0.4 |
|
|
0.3 |
|
|
0.2 |
σ |
|
0.1 |
|
0 |
|
|
|
|
1.57 |
3.14 |
4.71 |
|
|
-0.1 |
|
|
-0.2 |
|
|
-0.3 |
|
|
-0.4 |
|
|
-0.5 |
|
Рис. 47.2 |
|
Зависимость безразмерного инкремента Im x от параметра плотности пучка σ вблизи порога развития неустойчивости. Сплошная линия – аналитическое решение (47.10), пунктирная
– численное решение уравнения (47.9)
233
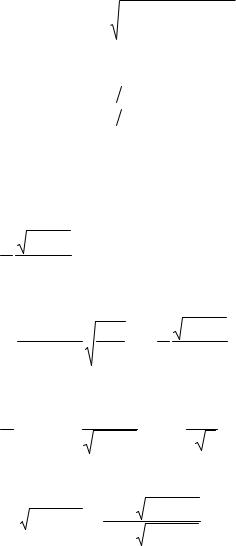
Александров А.Ф., Кузелев М.В. Физика электронных пучков
λmax = 4L - на длине резонатора помещается четверть длины волны возмущения, а значит минимальное волновое число дается соотношением
k |
min |
= |
2π |
= |
π |
. |
(47.13) |
λmax |
|
||||||
|
|
|
2L |
|
|||
Из (47.12) и (47.13) следует, что неустойчивость в конечной системе возможна при условии
kmin = |
π |
< |
|
a |
, |
(47.14) |
|
2L |
U |
||||||
|
|
|
|
||||
что совпадает со стартовым условием (47.6). Таким образом, порог (47.6) обусловлен невозможностью развития абсолютной неустойчивости в конечной системе при её малой длине. Затухание же волн в такой системе (мнимая часть частоты, как видно из (47.7) и Рис. 47.1
может |
быть отрицательной) связано, |
конечно, с вытеканием |
излучения через границы |
|||||||||
z = 0, |
z = L . |
|
|
|
|
|
|
|
|
|
|
|
|
Перейдем к рассмотрению более общего случая |Vg |≠U , |
но по-прежнему при κ2 = 0 . |
||||||||||
Вводя обозначения |
|
|
|
|
|
|
|
|
|
|||
|
ξ = |
U |
, χ0 |
= |
1 |
|
1 |
ω2 (1 +ξ)2 |
+ξa2 , |
(47.15) |
||
|
| Vg | |
|
4 |
|||||||||
|
|
|
|
U |
|
|
|
|
||||
представим уравнение (47.1) в виде |
|
|
|
|||||||||
|
exp(2iχ0 L)= |
ω |
(1+ξ) 2 + χ0U |
. |
|
(47.16) |
||||||
|
ω |
(1+ξ) 2 − χ0U |
|
|||||||||
|
|
|
|
|
|
|
||||||
Как и (47.2) уравнение (47.16) имеет решения ω = 0 , если 2χ0 L = π(2n +1) - см. (47.3). От-
сюда следует пороговое условие возникновения неустойчивости на продольной моде n = 0 , обобщающее условие (47.6)
a > |
π |
|Vg |
|U |
(47.17) |
2 |
L |
. |
||
|
|
|
Выражение для частоты вблизи порога на моде n = 0 дается формулой (см. (47.7))
ω = ia |
|
2L |
U |
|
|
− |
π |
|Vg |
|U |
|
|||
(|V |
|
| +U ) |
|V |
|
a |
2 |
L |
|
|
. |
|||
|
g |
g |
| |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Вводя аналоги величин (47.8) |
|
|
|
|
|||||||||
x = ω |
, σ = 2a |
L |
|
, µ = |
1+ξ |
, |
|
||||||
a |
|
|
|
|Vg |U |
|
|
|
2 |
ξ |
|
|
||
преобразуем уравнение (47.11) к следующему виду:
exp(iσ 1+ µ2 x2 )= |
µx + |
1 |
+ µ2 x2 . |
|
µx − |
1 |
+ µ2 x2 |
(47.18)
(47.19)
(47.20)
234

Александров А.Ф., Кузелев М.В. Физика электронных пучков
Заменой µx → x уравнение (47.20) сводится к (47.9), поэтому ничего нового, в сравнении с
приведенным на Рис. 47.1, численные решения уравнения (47.20) не содержат.
Учтем теперь конечное отражение от продольных границ системы. Подставляя реше-
ние (46.2) в общие граничные условия (45.16) при κ1,2 |
≠ 0 , получим следующее характери- |
|||||||||||
стическое уравнение: |
|
|
|
|
|
|
|
|
|
|||
exp(i(k |
− k |
|
)L)= |
ω − k2U |
+κ κ |
(k2 − k1 )U |
exp(i(k |
|
− k |
|
)L). |
(47.21) |
|
|
|
|
|||||||||
1 |
|
2 |
|
ω − k U |
1 2 (ω − k U ) |
3 |
|
2 |
|
|
||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
Заметим, что при нулевой плотности пучка ( a = 0 ) из уравнения (47.21), как это и должно быть, следует решение (46.7). Как и при нулевом отражении, случай различных скоростей волн сводится к случаю |Vg |=U , рассмотрением которого мы здесь и ограничимся. Кроме того, считаем для простоты, что κ1κ2 =κ > 0 , где κ - положительная вещественная постоян-
ная. Используя величины (47.8), преобразуем уравнение (47.21) к виду, удобному для дальнейшего анализа:
exp(iσ |
1+ x |
2 |
)= |
x + 1+ x2 |
2 1+ x2 |
|
σ |
1+ x |
2 |
|
|
σ |
|
(47.22) |
|
|
x − 1 |
−κ |
x − 1+ x2 |
exp i |
2 |
|
exp i |
2 |
x . |
||||||
|
|
|
|
+ x2 |
|
|
|
|
|
|
|
||||
Сначала определим пороги развития неустойчивости. Для этого, полагая в уравнении |
|||||||||||||||
(47.22) x = 0 , сведем его к виду |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
(47.23) |
exp(iσ) = −1+ 2κ exp i |
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Последнее уравнение, поскольку κ2 ≤1, преобразуется к следующему: |
|
|
|||||||||||||
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(47.24) |
cos |
= κ . |
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если расположить корни уравнения (47.24) относительно σ в порядке возрастания, то полу-
чатся пороговые условия развития неустойчивости на продольных модах n = 0 , |
n =1 и т.д. |
||
соответственно. Для моды n = 0 пороговое условие записывается в виде |
|
||
a > |
U |
arccos(κ) . |
(47.25) |
|
|||
|
L |
|
|
При κ = 0 неравенство (47.25) переходит в (47.6). Вблизи порога (47.25), учитывая неравенства x <<1 и (σ − 2 arccosκ) <<1, из уравнения (47.22) для безразмерной частоты получаем
x ≈ i σ / 2 − arccosκ . |
(47.26) |
1 + κ arccosκ |
|
1 −κ 2 |
|
Обобщением стартового условия начала генерации (47.25) на случай | Vg |≠ U очевидно яв-
ляется следующее (см. (47.17)):
235

|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|
a > |
U |
| Vg | |
arccos(κ) . |
(47.27) |
|
L |
|||||
|
|
|
|||
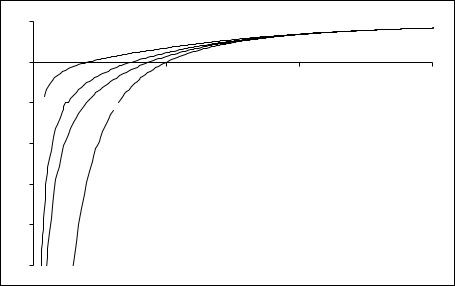
На Рис. |
47.3 представлены зависимости безразмерной частоты x |
для низшей про- |
|||
дольной моды n = 0 от параметра плотности пучка σ при различных коэффициентах отражения κ = 0, κ = 0.2, κ = 0.4 иκ = 0.8 , полученные численным решением уравнения (47.22).
Чем больше отражение κ , тем левее и выше расположена на Рис. 47.3 соответствующая кри-
вая Im x(σ) .
Из рисунков Рис. 47.1 и Рис. 47.3 следует, что при |
σ → ∞ имеет место предельное |
соотношение Im x →1, которое при | Vg |≠ U записывается |
в виде Im µx →1. Откуда, с уче- |
том определений (47.19), имеем
Imω →2a |
U | Vg | |
≤ a . |
(47.28) |
|
|||
L→∞ |
U + | Vg | |
|
|
|
|
|
Формула (47.28) дает инкремент глобальной неустойчивости при коллективном эффекте Че-
ренкова на встречной волне. При | Vg |=U он переходит в инкремент Imω = a неустойчиво-
сти, развивающейся в системе бесконечной длины. Заметим, что согласно общей теории неустойчивостей, пучковые неустойчивости на встречных волнах являются абсолютными, а неустойчивости на попутных волнах (см. предыдущий параграф) – конвективными.
§ 48. Генераторы попутных волн на одночастичном вынужденном эффекте Черенкова
Перейдем теперь к одночастичному вынужденному эффекту Черенкова в ограничен-
ной области пространства. Рассмотрение начнем со случая Vg > 0 , когда излучаемая волна распространяется в ту же сторону, что и пучок, т.е. является попутной. Представляя решения уравнений (45.12), (45.14) в экспоненциальной форме ~ exp(−iωt +ikz) , получим следующие дисперсионные уравнения:
D1 |
(ω, k) ≡ (ω − kU )2 (ω − kVg )− b3 = 0, |
(48.1) |
|
D2 (ω, k) ≡ (ω + kVg )= 0. |
|||
|
|||
Используя (48.1), запишем общее решение уравнений (45.12), (45.14) в виде (без общего множителя exp(−iωt) ):
|
Aw (z) = Aexp(ik1 (ω)z)+ B exp(ik2 (ω)z)+ C exp(ik3 (ω)z), |
|||||
|
b3 |
|
b3 |
|
b3 |
|
Ab (z) = |
|
Aexp(ik1 (ω)z)+ |
|
B exp(ik2 (ω)z)+ |
|
C exp(ik3 (ω)z), (48.2) |
(ω − k U )2 |
(ω − k U )2 |
(ω − k U )2 |
||||
|
1 |
|
2 |
|
3 |
|
Bw (z) = D exp(ik4 (ω)z).
236
Александров А.Ф., Кузелев М.В. Физика электронных пучков
1 |
Im x |
|
|
|
0 |
|
|
|
σ |
|
|
|
|
|
|
0 |
3.14 |
6.28 |
9.42 |
-1 |
|
|
|
|
-2 |
|
|
|
|
-3 |
|
|
|
|
-4 |
|
|
|
|
-5 |
|
|
|
|
|
|
|
Рис. 47.3 |
|
Зависимости мнимой частоты Im x низшей продольной моды n = 0 от параметра |
||||
плотности пучка σ при различных коэффициентах отражения: κ = 0, κ = 0.2, κ = 0.4, κ = 0.8 |
||||
237
Александров А.Ф., Кузелев М.В. Физика электронных пучков
где k1,2,3 (ω) - решения первого уравнения (48.1) относительно k , а k4 = −ω Vg - решение вто-
Vg - решение вто-
рого уравнения (48.1). |
|
|
|
|
|
|
|
|||
Чтобы не записывать сложных решений |
кубического дисперсионного |
уравнения |
||||||||
D1 (ω, k) = 0 |
получим некоторые полезные для дальнейшего формулы. Дифференцируя пер- |
|||||||||
вое уравнение (48.1) по ω находим соотношения |
|
|
|
|
||||||
|
∂k1,2,3 |
(ω) = |
k(U + 2Vg ) −3ω |
, |
∂k1,2,3 |
(0) |
= |
(U + 2Vg ) |
≡Wg−1 . |
(48.3) |
|
∂ω |
3kUVg −ω(2U +Vg ) |
|
|
||||||
|
|
|
∂ω |
|
3UVg |
|
||||
В некоторой области частот ω решения первого уравнения (48.1) являются комплексными,
причем два из решений комплексно-сопряженные. Пусть, например Im k2 (ω) < 0 , тогда функция exp(ik2 (ω)z) нарастает в положительном направлении оси Z . То есть волновое число k2 (ω) принадлежит усиливаемой волне. При этом из (48.3) следует, что максимум усиления, т.е. максимум | Im k2 (ω) |, достигается при ω = 0 . В окрестности нулевой частоты решения первого дисперсионного уравнения (48.1) очевидно записываются следующим образом:
k |
(ω) = k |
|
(0) +ω ∂k1,2,3 |
(0) = δ |
|
σ + ω |
, |
|||
1,2,3 |
1,2,3 |
|
|
∂ω |
|
|
1,2,3 |
Wg |
|
|
|
|
|
|
|
|
|
|
(48.4) |
||
|
b |
|
|
|
1−i |
3 , |
1+i |
3 , −1. |
||
σ = |
, |
δ1,2,3 |
= |
|
||||||
|
3 U 2Vg |
|
|
|
2 |
|
|
2 |
|
|
Используя (48.4), выпишем еще условие, при котором излучение пучка можно действительно считать одночастичным эффектом Черенкова. Для этого решения k1,2,3 следует подставить в
(45.11). В результате получится следующее неравенство:
b(U Vg )1 3 >> Gb ωb , |
(48.5) |
означающее, что плотность электронного пучка должна быть достаточно малой ( b ~ ωb2 3 ).
3 ).
Неравенство (48.5) является аналогом неравенства (39.11).
Перейдем теперь к выводу характеристического уравнения для определения собственных частот ω , рассматриваемой системы конечной длины. Подставляя решения (48.2) в граничные условия (45.17) и используя первое уравнение (48.1), получим следующую линейную однородную систему относительно постоянных A, B,C и D :
A + B + C = κ1D,
k1 A + k2 B + k3C = (ω Vg )κ1D,
k12 A + k22 B + k32C = (ω Vg )2 κ1D, (48.6) exp(ik1L) A + exp(ik2 L)B + exp(ik3 L)C = κ2−1 exp(ik4 L)D.
Предположим, что выполнено неравенство
238
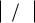
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
ω Vg << σ , |
(48.7) |
которое согласуется с формулами (48.4) и означает, что имеет место максимальное усиление одной из волн. Тогда правые части второго и третьего уравнений в (48.6) можно положить равными нулю. Выражая при этом из первых трех уравнений (48.6) А, В и С имеем:
A =α1κ1D, |
α1 |
= |
|
|
k2k3 |
, |
|
|
(k2 |
− k1 )(k3 − k1 ) |
|
||||||
|
|
|
|
|
|
|||
B =α2κ1D, |
α2 |
= |
|
|
k1k3 |
|
, |
(48.8) |
|
(k1 |
− k2 )(k3 − k2 ) |
||||||
|
|
|
|
|
|
|||
C =α3κ1D, |
α3 |
= |
|
|
k2k1 |
|
. |
|
|
(k1 |
− k3 )(k2 − k3 ) |
|
|||||
|
|
|
|
|
|
|||
Исключая далее с помощью (48.8) из последнего уравнения (48.6) постоянные А, В, С и D, находим следующее характеристическое уравнение для определения собственных комплексных частот системы:
exp(ik4 L) = κ1κ2 [α1 exp(ik1L) +α2 exp(ik2 L) +α3 exp(ik3 L)]. |
(48.9) |
При b = 0 , т.е. когда электронного пучка нет, уравнение (48.9) |
сводится, как это и |
должно быть, сводится к (46.7) (предельный переход b → 0 выводит за рамки неравенства (48.7) и применимости формул (48.4), поэтому должен совершаться не в (48.9), а в точной системе уравнений (48.6)).
Пусть теперь b ≠ 0 и выполнено неравенство (48.7). Тогда, подставляя (48.4) в (48.8),
получим |
|
|
|
|
α1 =α2 |
=α3 |
= |
1 . |
(48.10) |
|
|
|
3 |
|
Подставляя далее (48.4) и (48.10) в (48.9), сведем уравнение для собственных частот к виду
|
|
|
|
|
|
ω |
|
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|||||
exp |
−i |
L |
κ κ |
(exp(iδ σL) + exp(iδ σL) + exp(iδ σL))exp i |
L . |
||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
Vg |
|
|
|
|
|
3 |
1 |
2 |
|
|
|
1 |
2 |
|
3 |
|
Wg |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Откуда для комплексной собственной частоты ω имеем выражение |
|
|
|||||||||||||||||||||||||||
|
|
|
L |
|
|
|
|
L |
−1 |
|
|
1 |
|
|
|
3 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ω = i |
|
|
|
+ |
|
|
|
|
|
|
ln |
|
|
| κ1κ2 | |
∑exp(iδ jσL) |
|
+φ . |
|
|
|
|||||||||
|
|
|
W |
|
|
3 |
|
|
|
||||||||||||||||||||
|
|
|
V |
g |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∂k |
|
|
|
|
−1 |
|
|
3UV |
g |
|
|
|
|
|
|
|
||||||||||
W |
g |
= |
|
|
1,2 |
(0) |
= |
|
|
|
|
|
, |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
∂ω |
|
|
|
|
|
|
U + 2Vg |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(48.11)
(48.12)
(48.13)
входящая в (48.12) и введенная в (48.3), называется групповой скоростью сноса волн при усилении в режиме одночастичного эффекта Черенкова на попутной волне (для коллективного эффекта Черенкова на попутной волне аналогичная скорость определена в (46.10)).
239

|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|||||||
В длинной системе, у которой |
|
|
|
||||||||
σL >>1, |
|
|
|
|
|
|
|
|
|
|
(48.14) |
инкремент (48.12) принимает вид |
|
|
|
||||||||
L |
+ |
L |
|
−1 |
3 |
σL − ln |
3 |
|
(48.15) |
||
Imω = |
|
W |
|
|
|
2 |
| κ κ |
. |
|||
V |
g |
|
g |
|
|
|
| |
|
|||
|
|
|
|
|
|
|
1 2 |
|
|
||
Отсюда получаем стартовое условие начала генерации |
|
||||||||||
3 σL > ln |
|
3 |
|
| |
. |
|
|
|
|
(48.16) |
|
2 |
|
| κ κ |
2 |
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
при одночастичном эффекте Черенкова на попутной волне в резонаторе длины L . Известно, что одночастичный эффект Черенкова на попутной волне является конвек-
тивной неустойчивостью, при которой любые финитные возмущения сносятся по движению пучка и в каждой фиксированной точке пространства при t → ∞ из-за сноса затухают. Наличие границ препятствует сносу возмущений и при выполнении порогового условия (48.16) приводит к их нарастанию в любой точке z на отрезке [0, L] .
Совершая в (48.15) предельный переход L → ∞ , получим инкремент глобальной неустойчивости при одночастичном черенковском взаимодействии электронного пучка с попутной волной
Imω → |
3 |
b |
1 |
33 UVg2 |
. |
(48.17) |
L→∞ |
2 |
|
2 (2U +Vg ) |
|
|
|
|
|
|
|
|||
Максимального значения Imω = b 3 4 глобальный инкремент достигает при Vg =U , что в
два раза меньше инкремента обычной одночастичной пучковой неустойчивости в системе бесконечно большой длины.
Приведем еще один метод вычисления комплексной частоты (48.12). Пусть на границах z = 0 и z = L амплитуда попутной электромагнитной волны дается соотношениями (46.13) и (46.14) соответственно. Очевидно, что эти соотношения связаны между собой уравнением обратной связи (46.15). Несложно показать (например, используя (48.2)), что общее решение уравнений (45.12) c граничными условиями (46.13) и первыми двумя условиями (45.17) имеет вид
|
1 |
|
|
z |
3 |
|
Aw (z,t) = |
|
ψ |
|
|
|
(48.18) |
3 |
t − |
|
∑exp(iδ jσz) , |
|||
|
|
|
Wg j=1 |
|
||
где Wg - скорость (48.13), а σ и δ j приведены в (48.4). Подставляя (46.13) и (48.18) в соот-
ношение (46.15), получим функциональное уравнение
240
