
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
||
AIl (kz r), r < a |
|
|
|
|
|
|
Kl (kz R) , a < r < R . |
(43.4) |
|
ψ (r) = |
||||
B Kl (kz r) − Il (kz r) |
|
|
|
|
|
|
|||
|
|
Il (kz R) |
|
|
Здесь A и B - постоянные, а Il (x) и Kl (x) - функции Инфельда и Макдональда соответствен-
но. При записи решения (43.4) в области r > a полагалось, что при r = R имеется металлический кожух, на котором потенциал ψ (r) равен нулю.
На границе r = a непрерывен потенциал |
|
|
ψ (a + 0) −ψ (a − 0) = 0 , |
(43.5) |
|
а кроме того на этой границе имеет место соотношение |
|
|
′ |
′ |
(43.6) |
ε(a + 0)ψ (a + 0) −ε(a |
− 0)ψ (a − 0) = 0 , |
|
которое получается интегрированием уравнения (43.1) в окрестности точки r = a (штрихом обозначено дифференцирование по r). Подставляя решения (43.4) в условия (43.5) и (43.6) и исключая постоянные A и B , получим следующее дисперсионное уравнение:
|
|
Il+1 (kz a) |
|
|
Kl+1 (kz a) |
1 |
+ |
|
Kl (kz R) |
|
|
|
Il+1 (kz a) |
|
|
|
|
|
|
|
|
||||||
ε |
|
+ε |
|
|
|
Il (kz R) Kl+1 (kz a) |
|
= |
l |
(ε |
|
−ε |
) . |
(43.7) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 Il (kz a) |
|
2 Kl (kz a) |
|
1− |
|
Kl (kz R) |
|
Il (kz a) |
|
|
|
kz a |
|
2 |
1 |
|
|
|||||||||
|
|
|
|
Il (kz R) Kl (kz a) |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε1,2 =1 − |
|
Lb1,2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(43.8) |
||||
(ω − k u |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
z |
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проанализируем уравнение (43.7) в различных предельных случаях. В длинноволно-
вом пределе, когда kz a >>1, уравнение сводится к виду ε1 +ε2 = 0 , или
2 − |
ω2 |
|
− |
ω2 |
|
|
= 0 . |
(43.9) |
Lb1 |
|
Lb2 |
|
|||||
(ω − k u )2 |
(ω − k |
u |
)2 |
|||||
|
z |
1 |
|
z |
2 |
|
|
|
Но последнее уравнение элементарными подстановками можно свести к исследованному нами ранее дисперсионному уравнению (32.4) пучково-плазменной неустойчивости. Следовательно, и уравнение (43.9) имеет решения с Imω > 0 , т.е. описывает неустойчивую систе-
му. Функция (43.4) затухает в обе стороны от границы r = a (при kz a >>1 это затухание экс-
поненциальное). Поэтому неустойчивость, описываемая уравнением (43.9), обусловлена возбуждением поверхностной волны на границе проскальзывающих относительно друг друга электронных потоков. Ее называют slipping-неустойчивость. Напомним, что уравнение (32.4) описывает неустойчивость, связанную с возбуждением объемной волны. То есть при всем формальном математическом сходстве уравнения (32.4) и (43.9) относятся к существенно различным физическим системам: уравнение (43.9) учитывает поперечные движения про-
211
Александров А.Ф., Кузелев М.В. Физика электронных пучков
дольной границы раздела двух соприкасающихся пучков; уравнение (32.4) учитывает только продольные движения двух взаимопроникающих потоков.
Не сложно показать, что комплексные относительно ω решения у уравнения (43.9) имеются при выполнении условия
|
kz (u2 − u1 ) < [(ωLb2 |
1 |
|
2)1 3 + (ωLb2 |
2 2)1 3 ]3 2 . |
(43.10) |
||||||||
В частности, если плотности пучков по обе стороны раздела одинаковы, ωLb1 = ωLb2 |
= ωLb , то |
|||||||||||||
неустойчивость имеет место при |
|
|
||||||||||||
|
kz (u2 −u1 ) |
|
< 2ωLb . |
|
|
|
(43.11) |
|||||||
|
|
|
|
|
||||||||||
Максимальный инкремент |
|
|
||||||||||||
Imω = |
ωLb |
|
|
|
|
|
|
(43.12) |
||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
||
достигается при |
|
|
|
|
|
|
|
|
|
|
||||
kz = ± |
3 2 |
ωLb |
|
. |
|
|
|
(43.13) |
||||||
u2 −u1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Еще один интересный физический результат можно получить из уравнения (43.9). |
||||||||||||||
Полагая ωLb1 = ωLe , u1 = 0, ωLb2 = ωLb , u2 = u , запишем это уравнение в виде |
|
|||||||||||||
2 − |
ω |
2 |
|
|
|
|
ω2 |
|
|
|
= 0 . |
|
|
|
|
Le − |
|
|
|
Lb |
|
|
|
|
(43.14) |
||||
|
(ω − kzu)2 |
|
|
|||||||||||
|
|
ω2 |
|
|
|
|
|
|||||||
При ωLb = 0 решения последнего уравнения ω = ±ωLe 2 дают коротковолновую асимпто-
тику спектров частот поверхностных волн плазменного столба. При ωLb2 << ωL2e |
решение |
|||||
уравнения (43.14) можно искать в виде |
|
|||||
ω = ωLe 2 +δω = kzu +δω . |
(43.15) |
|||||
После элементарных вычислений для комплексного инкремента δω находим |
|
|||||
δω = −1 + i |
|
2 |
|
1 3 |
ωLe . |
(43.16) |
3 |
ωLb |
|
|
|||
2 |
|
2 |
|
|
2 |
|
|
2ωLe |
|
|
|||
Поскольку неустойчивость с инкрементом (43.16) развивается при резонансе kzu = ωLe 2 ,
то она очевидно обусловлена одночастичным вынужденным черенковским излучением пучком поверхностной волны ограниченной плазмы. Инкремент (43.16) имеет смысл сопоставить с инкрементом, приведенным в формуле (32.11).
В противоположном длинноволновом пределе, когда kz R <<1, уравнение (43.7) пре-
образуется к следующему виду:
212

|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
||
ε1+ε2 |
2 |
|
= 0 , l = 0, |
|
|
kz2a2 ln(R a) |
(43.17) |
||||
|
|
1 + (a R)2l |
|
. |
|
ε +ε |
|
= 0 , l =1,2,... |
|
||
|
1− (a R)2l |
|
|||
1 |
2 |
|
|
|
|
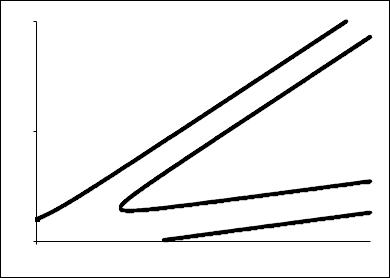
Мы не будем здесь приводить решений уравнений (43.17), поскольку существенно нового по сравнению с уже изложенным не возникает. На Рис. 43.1 изображены дисперсионные кривые первого уравнения (43.17) для системы с вполне реальными параметрами. Видно, что в длинноволновой части спектра ( kz R < 0.5) расположена область slipping-неустойчивости.
Топология дисперсионных кривых, изображенных на Рис. 43.1, такая же, как и кривых, представленных на Рис. 32.1.
Рассмотренная slipping-неустойчивость является сильной, в том смысле, что ее инкремент может быть того же порядка, что и вещественная часть частоты. Действительно, в
случае, когда инкремент дается формулой (43.12) имеем Reω ~ ωLb . Данное обстоятельство связано с тем, что скорость u(r) в некоторой точке меняется скачком. Иная неустойчивость
имеет место в случае, когда скорость u(r) является медленно меняющейся функцией коор-
динаты. Для исследования этой неустойчивости запишем дифференциальное уравнение
(43.1) для случая ωLb2 (r) = const |
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
||||
[(ω − k |
u(r))2 |
−ω2 |
] |
1 |
|
d |
|
r |
dψ |
− |
l |
|
ψ − k 2ψ |
= 2k |
|
ωLb |
|
du |
|
dψ |
. |
(43.18) |
|
|
|
|
r2 |
|
|
|
|
||||||||||||||||
z |
|
Lb |
r dr dr |
z |
|
|
z |
(ω − kzu(r)) dr dr |
|
||||||||||||||
Если скорость постоянна, т.е. |
u(r) = u0 |
= const , |
то из уравнения (43.18) получаются |
||||||||||||||||||||
спектры частот объемных пучковых волн плотности заряда – быстрой и медленной (см. § 27)
ω = kzu0 ±ωLb . |
(43.19) |
Потенциал этих волн следует задать в виде ψ (r) ~ Jl (k r) , где k = µls |
R , Jl (x) - функция |
Бесселя, а µls - ее корень. Заметим, что уравнения (43.18) с нулевой правой частью и условия
ψ (R) = 0 не достаточно для определения потенциала поля объемных волн пространственно-
го заряда пучка. Необходимо учесть хоть маленькое, но все же не нулевое внешнее магнитное поле. Однако подробно обсуждать этот вопрос мы здесь не имеем возможности.
Определим поправки к спектрам (43.19), связанные с отличием правой части уравне-
ния (43.18) от нуля. Положим для определенности |
|
|||
u(r) = u0 + ∆u |
r |
, |
(43.20) |
|
R |
||||
|
|
|
||
где ∆u - постоянная, которую считаем малой. Будем действовать методом последовательных приближений по ∆u . Умножим обе части уравнения (43.18) на собственную функцию ψ (r)
213
Александров А.Ф., Кузелев М.В. Физика электронных пучков
1 ω
0.5
k z
0 

 0 0.5 1
0 0.5 1
Рис. 43.1
Дисперсионные кривые уравнения (43.17) для l = 0 :
ωb1 = ωb2 =109 рад/ c, u1 = 2 109 см/ с, u2 =1010 см/ с, a =1см, R = 2см.
214

Александров А.Ф., Кузелев М.В. Физика электронных пучков
и проинтегрируем его по rdr в пределах от нуля до R . При этом в левой части пренебрежем ∆u в результате чего получим
[(ω − kzu0 )2 −ωLb2 ](k 2 + kz2 ) |
|
|
|
ψ |
|
|
|
2 = −kz ∫R |
ωLb2 |
|
du dψ 2 |
rdr . |
(43.21) |
||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 (ω − kzu(r)) dr dr |
|
|
|||||
Здесь ψ

 - норма собственной функции. Причем при подстановке в соотношение (43.21) соб-
- норма собственной функции. Причем при подстановке в соотношение (43.21) соб-
ственной функции следует взять функцию нулевого приближения Jl (k r) .
Очевидно, что вклад правой части в соотношение (43.21) существенен только если при некотором r разность ω − kzu(r) проходит через ноль (в противном случае правая часть
(43.21) пропорциональна ∆u ). Но при ω − kzu(r) → 0 под интегралом в (43.21) возникает особенность. Для ее устранения используем правило Ландау, для чего полагаем ω = ω + iδ , где δ → +0 . В результате имеем
ω − k |
u(r) ≈ ±ω |
Lb |
+ k |
z |
[u |
0 |
−u(r)]+ iδ = −(r − r )k |
z |
du(r0 ) |
+ iδ , |
(43.22) |
|
|||||||||||
z |
|
|
|
0 |
dr |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
где r0 - корень уравнения |
|
|
|
|
|
|
|
|
|||
±ωLb |
+ kz [u0 − u(r)]= 0 . |
|
|
|
|
(43.23) |
|||||
При получении (43.22) было использовано дисперсионное уравнение (43.19) нулевого по ∆u приближения.
Подставляя (43.22) в правую часть соотношения (43.21) и совершая предельный переход δ → +0 , получим
R |
αωLb2 |
|
dψ 2 |
2 |
dψ02 |
|
|
∫ |
|
|
|
rdr ≈ iπωLbr0 |
|
. |
(43.24) |
α(r − r ) − iδ |
|
dr |
dr |
||||
0 |
0 |
|
|
|
|
|
|
Здесь α = kz du dr = kz ∆u R , а ψ0 =ψ (r0 ) . При вычислении (43.24) была использована из-
вестная формула Сохоцкого. С учетом (43.24) из (43.21) находим следующее дисперсионное уравнение первого по ∆u приближения:
(ω − kzu0 )2 −ωLb2 |
= iπωLb2 |
r dψ 2 |
dr |
2 . |
(43.25) |
|
0 0 |
|
|||||
|
|
|
(k 2 + kz2 )ψ |
|
|
|
Будем искать решение уравнения (43.25) в виде |
|
|||||
ω = kzu0 ±ωLb +δω , | δω | << ωLb , |
|
(43.26) |
||||
где δω - мнимая поправка к частоте. Подставляя (43.26) в (43.25), имеем |
|
|||||
δω = ±iπωLb |
r dψ 2 dr |
2 . |
|
|
(43.27) |
|
0 |
0 |
|
|
|||
(k 2 |
+ kz2 )ψ |
|
|
|||
|
|
|
|
|
||
Преобразуем последнюю формулу к более простому виду. Из (43.23) и (43.20) находим
215

Александров А.Ф., Кузелев М.В. Физика электронных пучков
k 2 = ω2 R2 |
|
(∆u)2 r2 . |
|
|
|
|
(43.28) |
||||||||
z |
Lb |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Поскольку |
здесь |
|
малая |
|
величина |
∆u входит в знаменатель, естественно |
считать, что |
||||||||
kz2 >> k 2 . Тогда выражение (43.27) для δω записываем в следующем виде: |
|
||||||||||||||
δω = ±iπ |
|
1 |
|
∆u |
|
2 r2 |
r |
dψ |
2 |
. |
(43.29) |
||||
|
|
|
|
|
|
0 |
|
|
0 |
||||||
|
|
|
|
|
|
|
|||||||||
|
|
ωLb R |
|
|
|
ψ |
2 |
0 dr |
|
|
|
||||
В качестве иллюстрации приведем выражение для δω в случае азимутально симметричных возмущений системы
δω = mi4π |
1 |
|
∆u 2 |
r |
3 |
J |
|
(µ |
r R)J |
(µ |
r R) |
. |
(43.30) |
||
|
|
|
|
0 |
|
|
0 |
|
0s 0 |
1 |
|
0s 0 |
|||
|
ωLb |
R |
|
R |
|
|
|
|
J12 (µ0s ) |
|
|
|
|||
В зависимости от взятого в (43.30) знака и от знака произведения функций J0 (x)J1 (x)
возможно как затухание возмущений, так и их раскачка, т.е.неустойчивость. И нарастание и затухание возмущений обусловлены резонансным черенковским взаимодействием (взаимодействие волна-частица) между волной (43.12) пространственного заряда пучка и слоем ре-
зонансных электронов, для которых выполнено условие ω − kzu(r0 ) = 0 . Явление вполне ана-
логично прямому и обратному затуханиям Ландау. Разница только в том, что затухание Ландау обусловлено тепловым разбросом частиц по скоростям, а резонансная slippingнеустойчивость обусловлена различием скоростей частиц из-за пространственной неоднородности потока. Условие применимости формул (43.29) и (43.30) сводятся, как это следует из (43.26), к неравенству
|
∆u 2 |
r |
3 |
|
||
4π |
|
|
0 |
|
<< ωLb2 . |
(43.31) |
|
||||||
|
R |
|
R |
|
|
|
В силу (43.28) резонансная slipping-неустойчивость является коротковолновой. Одна-
ко, при большом значении производной du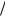 dr такая неустойчивость смещается в длинно-
dr такая неустойчивость смещается в длинно-
волновую область, а инкремент ее по порядку величины равен kz R du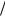 dr .
dr .
Учтем теперь наличие внешнего магнитного поля. Если это поле бесконечно велико,
то Ω2bε b → 0 и дифференциальное уравнение (40.18) записывается в виде
1 d |
r |
dψ |
− |
l2 |
ψ − k 2ε(r)ψ = 0 , |
(43.32) |
|||
|
|
|
|
|
|||||
r dr |
dr |
r2 |
|||||||
|
|
z |
|
||||||
где ε(r) дается формулой (43.2). Если распределения плотности и скорости электронов пуч-
ка определить формулами (43.3) и положить, например, u 1 = 0 , то уравнение (43.32) будет описывать колебания цилиндрической плазмы, обдуваемой полым электронным пучком. В такой системе возможна обычная пучково-плазменная неустойчивость, подробно рассмот-
ренная нами в § 37. Резонансные (ω − kzu(r) ≈ 0 ) раскачка и затухание возмущений описы-
216
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ваются уравнением (43.32) и при плавной зависимости u(r) . Однако, к явлениям типа slip- ping-неустойчивости мы эти процессы причислять не будем. Условимся для slippingнеустойчивостей считать важным как наличие градиента продольной скорости электронов, так и возможность их поперечного к направлению внешнего магнитного поля смещения. Поэтому запишем дифференциальное уравнение (40.18) для случая достаточно большого,
ωLb2 << Ωe2 , но все же конечного внешнего магнитного поля и для однородного по r распреде-
ления плотности электронов пучка
|
1 d |
dψ |
|
l |
2 |
|
2 |
|
|
2 |
|
|
l |
|
2 |
|
du(r) |
|
|
|||
|
|
|
|
|
|
ωLb |
|
|
|
ωLb |
|
|
|
|||||||||
|
|
|
|
r |
|
− |
|
ψ |
− kz |
1 |
− |
|
ψ |
= kz |
|
ψ |
|
|
|
. |
(43.33) |
|
r |
dr |
dr |
r2 |
(ω − kzu(r))2 |
r |
Ωe (ω − kzu(r))2 |
|
dr |
||||||||||||||
Проанализируем уравнение для случая малого градиента скорости u(r) , |
например, |
|||||||||||||||||||||
для распределения (43.20). Умножим обе части уравнения (43.33) на собственную функцию
ψ (r) и проинтегрируем его по rdr |
|
в пределах от нуля до |
R . При этом в знаменателях |
|||||||||||
ω − kzu(r) |
пренебрежем членами ~ kz ∆u по сравнению с ω . В результате чего получим сле- |
|||||||||||||
дующее дисперсионное уравнение: |
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
lkz |
|
|
2 |
|
∆u |
|
|
2 |
2 |
|
ωLb |
|
|
|
|
|
ωLb |
|
|
|
||
k |
+ kz |
1 − |
|
|
|
= − |
|
|
|
|
|
|
G , |
(43.34) |
(ω − kzu0 ) |
2 |
Ωe |
|
(ω |
− kzu0 ) |
2 |
R |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
где
G = ∫Rψ 2dr ∫R rψ 2dr ~ |
1 . |
|
0 |
0 |
R |
Из уравнения (43.34) для частоты ω находим
|
|
|
2 |
1 2 |
|
l ∆u |
|
ω = kzu0 |
|
|
kz |
|
1 − |
. |
|
±ωLb |
2 |
2 |
|
Ωekz R R |
|||
|
k |
+ kz |
|
|
|
||
(43.35)
(43.36)
Неустойчивость имеет место при выполнении неравенства |
|
||||||||||
| kz | < k0 |
≡ |
| l | |
|
| ∆u | |
. |
|
(43.37) |
||||
|
|
|
|
||||||||
|
|
|
|
R | Ωe | R |
|
||||||
При k0 < k максимальный инкремент достигается при kz = k0 |
2 и составляет |
||||||||||
δω = iω |
|
|
|
| l | |
|
|
| ∆u | |
. |
(43.38) |
||
|
|
|
|
|
|
|
|
||||
|
Lb 2k R | Ωe | R |
|
|||||||||
Рассмотренные неустойчивости приводят не только к выравниванию поперечного профиля скорости электронов пучка, но и к перемешиванию соседних слоев электронов. Последнее связано с возможностью поперечного смещения электронов в конечном внешнем магнитном поле. Поэтому при slipping-неустойчивости ламинарное движение электронов пучка становится турбулентным.
217

Александров А.Ф., Кузелев М.В. Физика электронных пучков
§ 44. Неустойчивость пучка с неоднородным поперечным профилем плотности - диокотронная неустойчивость
Данная неустойчивость развивается в частично нейтрализованном электронном пучке с радиально неоднородным профилем плотности и обусловлена его азимутальным вращением. Считаем, что нейтрализация пучка обеспечивается фоном бесконечно тяжелых ионов,
электроны фона отсутствуют, а продольная скорость электронов пучка Vbz(s) ≡ u постоянна в поперечном сечении. Ограничимся рассмотрением только длинноволновых возмущений, для чего в общем уравнении (40.18) положим продольное волновое число kz = 0 . Предположим также, что выполнены следующие неравенства:
ω −lωb(s) (r) 2 << Ωe2 γb2 ,
ωLb2 << Ωe2γb−1 , |
(44.1) |
[ωb(s) (r)]2 << Ωe2 γb2 . |
|
В условиях (44.1) и при kz = 0
записано в следующем виде:
|
1 |
|
d |
r |
d |
− |
l2 |
ψ = − |
l |
ψ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
dr |
|
r |
2 |
|
r |
|
|
r dr |
|
|
|
|
|
||||||
основное дифференциальное уравнение (40.18) может быть
1 |
|
dωLb2 (r) |
. |
(44.2) |
Ωe (ω −lωb(s) ) |
|
dr |
||
|
|
|
Рассмотрим трубчатый электронный пучок с профилем плотности, заданным формулой (см. распределение (23.13))
|
|
0, |
0 < r < rb1 |
|
|
|
ω2 |
(r) = |
ω2 |
= const, r |
≤ r ≤ r |
. |
(44.3) |
Lb |
|
Lb |
b1 |
b2 |
|
|
|
|
0, |
|
r > r |
|
|
|
|
|
|
b2 |
|
|
В силу последнего неравенства (44.1) пучок вращается с меньшей из двух возможных угловых скоростей (23.14), т.е.
|
(s) |
|
(−) |
|
Ωe |
|
|
|
2γ0ωLb2 |
|
|
2 |
)(1 |
|
2 |
|
2 |
1 2 |
|
|
|
||
ω |
|
(r) = ω |
|
(r) = |
|
|
1 − |
|
1 |
− |
|
(1 − f |
− β |
|
− r |
|
r |
|
|
|
, |
(44.4) |
|
|
b |
|
b |
|
2γ |
0 |
|
|
|
|
Ω2 |
|
|
0 |
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
где β0 = u c , γ0 = (1− β02 )−1
c , γ0 = (1− β02 )−1 2 . При малой плотности электронов пучка (см. второе неравенст-
2 . При малой плотности электронов пучка (см. второе неравенст-
во (44.1)) выражение для угловой скорости (44.4) упрощается
ωb(−) (r) = ωD (1− rb21 |
r2 ), ωD = |
ωLb2 |
(1− f − β02 ) , |
(44.5) |
|
2Ωe |
|||||
|
|
|
|
где ωD - угловая скорость, обусловленная дрейфовым движением электронов в скрещенных собственном электрическом и внешнем магнитном полях (см. (20.11) и (42.12)) и с учетом собственного азимутального магнитного поля.
Подстановка ступенчатого распределения (44.3) в правую часть уравнения (44.2) при218

Александров А.Ф., Кузелев М.В. Физика электронных пучков
водит к следующему уравнению:
1 d |
r |
d |
|
l2 |
|
l |
|
|
ωLb2 |
|
|
[δ(r − rb1 ) −δ(r − rb2 )] , |
(44.6) |
|||||
|
|
|
|
|
− |
|
ψ |
= − |
|
ψ |
|
|
|
|
||||
r dr |
|
dr |
|
r |
|
|
r |
|
Ωe (ω −lωb |
(r)) |
|
|
|
|||||
которое вне точек r = rb1 |
и r = rb2 |
является однородным. Общее решение однородного урав- |
||||||||||||||||
нения (44.6) есть линейная комбинация функций r l и r −l . Поэтому, если при r = R > r |
на- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
ходится металлический кожух, то решение уравнения (44.6), удовлетворяющее условиям |ψ (0) | < ∞ и ψ (R) = 0 , имеет вид
Arl , |
0 < r < rb1 |
|
|
rb1 < r < rb2 |
(44.7) |
ψ (r) = Brl + Cr−l , |
||
D(rl − R2l r−l ), rb2 < r < R |
|
|
Для исключения постоянных A, B, C, D следует использовать граничные условия в точках
r = rb1 и r = rb2 , в которых правая часть уравнения (44.6) имеет сингулярность. Первые два условия заключаются в непрерывности потенциала
ψ (rb1 |
+ 0) −ψ (rb1 |
− 0) = 0, |
(44.8) |
|
ψ (rb2 + 0) −ψ (rb2 − 0) = 0. |
||||
|
||||
Еще два условия получаются интегрированием с весом r уравнения (44.6) по бесконечно малым окрестностям особых точек правой части, что дает
ψ ′(rb1 + 0) −ψ ′(rb1 −0) = − |
l |
|
ψ (rb1 ) |
ωLb2 |
|
||||
|
Ωe (ω −lωb(−) (rb1 )) |
, |
|
||||||
rb1 |
(44.9) |
||||||||
|
l |
|
|
|
ωLb2 |
||||
ψ ′(rb2 +0) −ψ ′(rb2 −0) = |
ψ (rb2 ) |
|
|
||||||
|
Ωe (ω −lωb(−) (rb2 )) |
, |
|
||||||
rb2 |
|
||||||||
где штрихом обозначено дифференцирование по r. Как видно из (44.5) имеют место соотно-
шения ωb(−) (rb1 ) = 0 и ωb(−) (rb2 ) =ωD (1−rb21  rb22 ).
rb22 ).
Подставляя решение (44.7) в граничные условия (44.8) и (44.9) и исключая постоянные A, B, C, D , после простых, но довольно громоздких вычислений получим следующее
квадратное дисперсионное уравнение для определения собственных частот ω : |
|
||
(ω ωD )2 − a (ω ωD )+ b = 0 , |
|
(44.10) |
|
где |
|
|
|
a = l(1 − rb21 rb22 )+ ((rb2 R)2l − (rb1 |
R)2l ), |
(44.11) |
|
b = l(1 − rb21 rb22 )(1 − (rb1 R)2l )− (1 − (rb1 rb2 )2l )(1 − (rb2 R)2l ). |
|||
|
|||
Решение уравнения (44.11) имеет вид |
|
|
|
ω = ωD [a ± a2 − 4b]. |
|
(44.12) |
|
2 |
|
|
|
219
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Частоты (44.12) действительные, т.е. рассматриваемая система устойчива, если вы-
полнено неравенство a2 ≥ 4b . Не сложно показать, что для любых l условие устойчивости выполнено при rb1 = 0 , или при rb2 = R . Кроме того, не зависимо от значений радиусов rb1 , rb2 и R устойчивы возмущения с l = 0 и l =1 . Таким образом для возникновения неустой-
чивости необходимо наличие у пучка двух свободных границ. Можно считать, что неустойчивость, если она есть, обусловлена взаимодействием поверхностных волн, бегущих по внутренней и внешней границам пучка, движущимся относительно друг друга из-за шира угловой скорости (44.5). Инкремент данной неустойчивости, называемой диокотронной, по порядку величины, как это следует из (44.12), равен дрейфовой частоте ωD .
На Рис. 44.1 для примера построены безразмерные инкременты диокотронной неус-
тойчивости δ = 2 Imω ωD для трубчатого пучка в волноводе с R = 2см и различных радиу-
ωD для трубчатого пучка в волноводе с R = 2см и различных радиу-
сах rb1 и rb2 . Неустойчивость имеется только в конечном диапазоне азимутальных волновых чисел l . Причем, чем меньше толщина пучка, тем шире этот диапазон и больше инкремент:
при rb2 − rb1 = 0.1см неустойчивы моды с l от 2 до 13, а максимум инкремента δ = 0.725 дос-
тигается при l = 9 (кривая 1); при rb2 − rb1 = 0.6см неустойчивы только вторая и третья моды,
а максимум инкремента δ = 0.279 имеет вторая мода (кривая 4). С дальнейшим увеличением толщины пучка неустойчивость остается лишь на второй моде: при rb2 − rb1 =1см δ = 0.116 .
А при еще большей толщине неустойчивость совсем пропадает. Диокотронная неустойчивость приводит к поперечному расслоению трубчатого электронного пучка на токовые нити. Число нитей по-видимому совпадает с азимутальным числом l , на котором достигается максимум инкремента.
220
