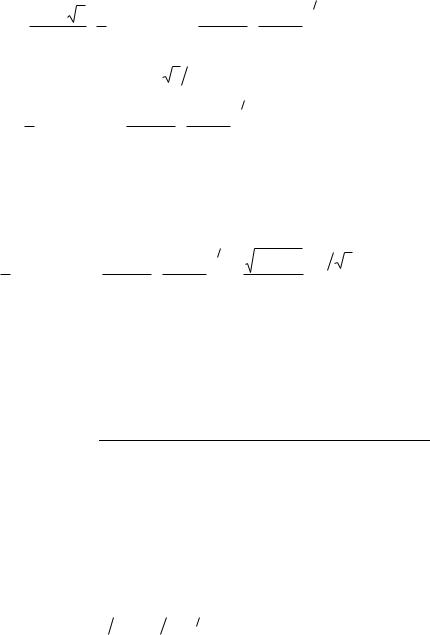27_VaN[1]

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

Аппаратные средства вычислительной техники

Файл:

t=0 = z0 ,

В линейном приближении полагаем

z′ = z0 +ξ,

v′ = u +ξ&.

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

4.53 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2627 / 2927 28 29 > Следующая >>>

Александров А.Ф., Кузелев М.В. Физика электронных пучков

dz′

= v

′

−u,

dv′

= −

ωLb2

γ ′−3 [ exp(−i∆1t

+ i(k + χ)z′)−C.С.]−

(52.19)

(k + χ)

e 2

−6

′

)−C.С.].

−

iE0

k sγ

′

2 +

[As exp(−i∆1t + i(k + χ)z

Ω0

∆0

Уравнения (52.13), (52.19) и соотношения (52.14), (52.17) являются основными для исследования вынужденного излучения в электростатическом ондуляторе и расчета лазеров на свободных электронах, основанных на этом излучении. Из (52.9) следуют начальные условия для уравнений движения электронов (52.19)

Малыми возмущениями, по которым уравнения ондуляторного излучения следует линеари-

зовать являются ξ, As , . При этом γ				′	= γ ,	ˆ	−3	, где γ - невозмущенный релятивист-
зовать являются ξ, As , . При этом γ					= γ ,	= γ		, где γ - невозмущенный релятивист-
ский фактор пучка, а
	2	z +L0	2
= −i exp(i∆1t)	2	∫(k + χ)ξ exp(−i(k + χ)z0 )dz0 .							(52.22)
= −i exp(i∆1t)	L	∫(k + χ)ξ exp(−i(k + χ)z0 )dz0 .							(52.22)
0		z −L	2
		0

Подставляя (52.21) в линеаризованные уравнения (52.19), исключая из них ξ&, умножая далее уравнение для ξ на exp(i∆1t) exp(−i(k + χ)z0 ) и интегрируя его по z0 на отрезке длиной L0 ,

получим с учетом (52.22) следующее уравнение для амплитуды волны плотности заряда пучка :

∂

+ u

∂

−i∆

= −ω

−3

−

−6

ω2

A .

(52.23)

Ω02

∂t

∂z

В (52.23) учтено, что согласно определению полной производной d dt = ∂ ∂t + u ∂ ∂z .

Объединяя с уравнением (52.23) уравнение (52.13) для амплитуды As

поля излучения,

получим следующую систему линейного приближения:

∂A

c2ω

2 γ −3

s +V

s = −i

4ω

s Ω02

∂t

g ∂z

(52.24)

∂

ω2

+ u

−i∆

= −ω

−3

−

−6

A .

Ω02

∂t

∂z

Последнее уравнение системы (52.24) можно расписать более подробно

∂

−3

e 2

−6

ω2

+ u

− 2i∆

+ u

− (∆

−ω

) = −

A . (52.25)

∂t

∂z

∂t

∂z

Ω02 s

261

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Очевидно, что аналогом первого уравнения системы (45.3) в случае ондуляторного излучения является ∆21 −ωLb2 γ −3 = (ω − ku − Ω0 )2 −ωLb2 γ −3 = 0 (второе уравнение (45.3) уже использо-

вано при получении уравнения для амплитуды As ). Поэтому окончательно систему (52.24)

можно записать в виде

∂

+ u

∂

−3 2

∂

+ u

∂

−6

ω2

∂t

m 2iω

∂t

= −

∂z

Ω02 s

(52.26)

∂A

c2ω2

γ −3

s +V

s = −i

∂t

g ∂z

4ω

s Ω02

Уравнения (52.26) по структуре в точности совпадают с системой (45.6). Поэтому результаты общего анализа, проведенного в главе IX без изменений переносятся на лазеры на свободных электронах, основанные на ондуляторном излучении релятивистского электронного пучка в электростатическом поле накачки. Сформулируем окончательные результаты.

Дисперсионное уравнение, которое следует из уравнений (52.26) при подстановке в них As , ~ exp(−iδω t + iδkz) , имеет вид

(δω −δkV

)(δω −δku)[(δω −δku) ± 2ω

−

3 2

] =

k 2

ωω2

−

3 .

(52.27)

χmu

Ω0

Максимальные инкременты получаются из (52.27) при δk = 0 . При выполнении неравенства

ωLb2 γ −3		eE0	k 2sc2
ω2	<<	χmu2γ 2	Gs Ω02	(52.28)

имеет место пучковая неустойчивость, обусловленная одночастичным ондуляторным излучением, инкремент которой дается формулой

δω =

−1+ i

k 2

ω2

−3 1 3

(52.29)

ω .

χmu

Ω0

Если выполнено неравенство противоположное (52.28), то неустойчивость обусловлена коллективным ондуляторным излучением и имеет следующий инкремент развития:

	1	eE0		2	2	ωLbγ	−3 2	1 2
	1	eE0		k sc		ωLbγ			ω .	(52.30)
δω =	4 i	χmu2γ 2	Gs	Ω02		ω			ω .	(52.30)

Применим формулы (52.29) и (52.30) для определения стартовых условий начала генерации в ондуляторе длины L . Учитывая связь Imω = a и используя формулу (52.30), найдем выражение для общего параметра (45.10) при коллективном ондуляторном излучении

	1	eE0		2	2	ωLbγ	−3 2	1 2
	1	eE0		k sc		ωLbγ			ω .	(52.31)
a =	4	χmu2γ 2	Gs	Ω02		ω			ω .	(52.31)

Аналогично, используя связь Imω = b 3 2 и формулу (52.29), для общего параметра (45.13) 262

Александров А.Ф., Кузелев М.В. Физика электронных пучков

имеем

b =	1			eE			2	k 2	c2	ω2	γ		−3 1 3		(52.32)
b =		G			0			s	2	Lb		2		ω .	(52.32)
	2		s	2		γ	2		2	ω		2
	2			χmu		γ		Ω0		ω

Подставляя (52.31) в общие условия (46.11) и (47.27), найдем стартовые условия начала генерации в ондуляторе в условиях коллективного эффекта

k 2

c2 ω

γ −3 2

1 2

arcch | κ κ

|−1,

ω = ω+ ,

> 4 ωL

1 2

χmu2γ 2

Ω2

arccos | κ κ

|−1,

ω = ω+. .

(52.33)

Здесь ω+1 > 0 и ω+2

> 0 - частоты, определенные в (51.9). При ω = ω+1

генерация происходит

на попутной волне (Vg

~ c > 0 ), а при ω = ω+2

генерируется встречная волна (Vg ~ −c < 0 , см.

Рис. 51.1).

Подставляя далее (52.32) в общие условия (48.16) и (49.6), получим стартовые условия начала генерации в ондуляторе в условиях одночастичного эффекта

		eE			2	k 2	c2	ω2	γ		−3 1 3
G			0			s	2	Lb		2
	s	2		γ	2		2	ω		2
		χmu		γ		Ω0		ω

>	u	(4 3) ln 3 \| κ κ			\|−1, ω = ω+	,	.	(52.34)
			2 p(\| κ1κ2	1 2	1
	ωL			\|),	ω = ω2+.

При получении (52.33) и (52.34) вместо групповой скорости излучаемой в ондуляторе волны

Vg в общие формулы была подставлена скорость света c , а при вычислении частот излуче-

ния отброшены поправки ~ ωLb , что справедливо при ω+1,2 >> ω , ωLbγ −32 .

§ 53. СВЧ генераторы на основе периодических волноводов

Излучение пучка электронов прямолинейно и равномерно движущихся в системе, параметры которой (диэлектрическая проницаемость, радиус и т.п.) являются периодическими функциями пространственных координат, аналогично ондуляторному излучению осциллирующих электронов. Формальная разница заключается в том, что в периодической системе осциллируют не сами электроны, а их изображения (т.е. заряды и токи, наведенные в системе движущимися электронами). В качестве примера рассмотрим излучение прямолинейного пучка электронов в гофрированном волноводе. Так называется симметричный металлический волновод кругового сечения, радиус которого периодически зависит от продольной ко-

ординаты z . В простейшем случае эта зависимость имеет следующий вид:
r(z) = R + h cos χz .	(53.1)
Глубину гофрировки h считаем малой, т.е.
h R <<1 ,	(53.2)

и ограничимся исследованием возбуждения пучком азимутально симметричных волновод263

Александров А.Ф., Кузелев М.В. Физика электронных пучков

ных волн E -типа. Поляризационный потенциал электромагнитного поля таких волн удовле-

творяют системе уравнений (см. (37.1))

∂

−

= −4πPb (r ) jb ,

∂r

∂z

∂t

∂t r ∂r

(53.3)

∂

ω2 γ −3

∂E

+ u

z .

∂t

∂z

4π ∂t

Компоненты электрического поля волны вычисляются по формулам

∂

∂ ψ

−

Er =

(53.4)

Ez =

∂z

∂t

ψ ,

∂r∂z

На металлической границе волновода r = r(z)

обращается в ноль тангенциальная со-

ставляющая электрического поля Eτ . Пусть α - угол между осью z и касательной к функ-

′
ции r(z) , тогда tgα = r (z) . Из простого геометрического построения следует, что на метал-
лической стенке волновода Eτ = Ez cosα + Er sin α .	Следовательно, граничное условие для
уравнений (53.3) записывается следующим образом:
(Ez + Er r′(z))r=r(z) = 0 .	(53.5)

С учетом (53.1) и (53.4), с точностью до квадратичных по малому параметру (53.2) членов, граничное условие (53.5) преобразуется к виду

∂

2 2

∂

1 + (cos χz)h

(cos χz) h

−

ψ −

∂r

∂r2

∂z2

∂t2

(53.6)

∂

∂2ψ

− hχ(sin χz) 1

+ (cos χz)h

= 0 .

∂r

∂r∂z r=R

Дифференциальное уравнение (53.3) для функции ψ (t, z, r) имеет постоянные коэф-

фициенты. Но из-за периодического по z характера граничного условия (53.6) это уравнение эквивалентно дифференциальному уравнению с коэффициентами, являющимися периодическими функциями z . Из теории дифференциальных уравнений с периодическими коэффициентами следует, что для функции ψ (t, z, r) имеет место следующее представление:

+∞
ψ (t, z, r) = exp(−iωt + ikz) ∑φn (r) exp(inχz) .	(53.7)

n=−∞

Подставляя решение (53.7) в систему уравнений (53.3), исключая из нее плотность тока пуч-

ка jb и используя ортогональность функций exp(inχz) , получим бесконечное множество обыкновенных дифференциальных уравнений для функций φn (r)

1 d

dφ

P (r)

ω2

γ −3

−κ

= −κ

(53.8)

r dr

n b

∆2n

264

Александров А.Ф., Кузелев М.В. Физика электронных пучков

где κn2 = (k + nχ)2 −ω2 c2 , ∆n = ω − ku − nχu , а n = 0, ±1, ± 2,... .

Уравнения (53.8) зацеплены между собой через граничное условие (53.6). При подстановке решения (53.7) в граничное условие (53.6) будем, используя неравенство (53.2),

учитывать зацепление только трех ближайших функций φn (r) : φn−1 (r) , φn (r) , φn+1 (r) . При этом будут учтены все члены вплоть до квадратичных по малому параметру hR . В резуль-

тате несложных вычислений получаем из (53.6) и (53.7) следующую систему зацепляющихся граничных условий:

	h	2		h
φn (r) +			φn′′(r) +		(Kn,n−1φn′−1	(r) + Kn,n+1φn′+1	(r))	= 0 ,	(53.9)
	4			2
							r=R

где Kn,m =[(k + nχ)(k + mχ) −ω2 c2 ]κn−2 .

Прежде чем приступить к анализу общей и довольно сложной краевой задачи (53.8), (53.9) сделаем некоторые замечания о собственных электромагнитных волнах вакуумного гофрированного волновода. Полагая ωLb2 = 0 и учитывая ограниченность поля при r = 0 , за-

пишем общее решение уравнений (53.8) в виде

φn (r) = An J0 (iκnr), n = 0, ±1, ± 2,... . (53.10)

Подставляя (53.10) в условия (53.9) получим следующую бесконечную систему однородных линейных алгебраических уравнений относительно постоянных An :

h	[Kn,n−1J0′(iκn−1R)]An−1		h	2		h	[Kn,n+1J0′(iκn+1R)]An+1 = 0 . (53.11)
		+ J0 (iκnr) +			J0′′(iκnr) An +
2			4			2

Бесконечный определитель системы (53.11) – он называется определителем Хилла – является

дисперсионным уравнением Dh (ω, k) = 0						для спектров частот ω(k)	собственных электро-
магнитных волнах вакуумного гофрированного волновода.
	При h = 0 дисперсионное уравнение оказывается очевидно следующим:
		+∞
	Dh=0 (ω, k) ≡ Π J0 (iκn R) = 0 .									(53.12)
		n=−∞
Уравнение (53.12) удовлетворятся если,						например, J0 (iκ0 R) = 0 , т.е.		ω2 = k 2c2 +ω2 , где
ω2	= k 2	c2 . Поскольку при этом J	0	(iκ	n≠0	R) ≠ 0 , то из (53.11) имеем	A		= 0 , а	A - произ-
	m		0		n≠0		n≠0			0

вольная постоянная. Таким образом из (53.10) и (53.11) при h = 0 следуют собственные частоты и собственные функции обычного вакуумного волновода кругового сечения.

При h ≠ 0 все коэффициенты An ≠ 0 , причем, если выполнено неравенство (53.2), то

A	= O(h R)n A +... .		(53.13)
±n		0
В частности A		= O(h R) A . Поправки к собственным частотам оказываются ~ (h R)2 и при
	±1	0
			265

Александров А.Ф., Кузелев М.В. Физика электронных пучков

hR <<1 не играют принципиальной роли (кроме сравнительно узких зон волновых чисел k

около точек ±(χ 2), ± 2(χ 2) и т.д., о чем см замечание ниже). Поэтому при малой глубине гофрировки, поскольку | ωk | > u , обычное черенковское излучение прямолинейного пучка в волноводе невозможно. Однако, из-за наличия в потенциале (53.7) пространственных гармоник с n ≠ 0 возможно резонансное взаимодействие пучка и поля при ω − ku − nχu ≈ 0 . В силу

(53.13) наиболее эффективным излучение будет в условиях резонанса (см. (51.8))

ω − ku m χu = 0,

ω2 − k 2c2 −ω2 = 0,

(53.14)

рассмотрением которого мы здесь и ограничимся (в первом уравнении (53.14) условимся в дальнейшем брать знак минус).

Заметим, что при достаточной глубине гофрировки, из-за резонансного взаимодейст-

вия пространственных гармоник с разными n , при k ≈ ±(χ 2), ± 2(χ 2),K происходит значи-

тельное замедление электромагнитных волн периодического волновода. В связи с чем появляется возможность обычного черенковского излучения. Соответствующие СВЧ излучатели, называемые карсинотронами, здесь не рассматриваются.

Записывая условие резонанса в виде ω − ku − χu ≈ 0 (см. (53.14)) и ограничиваясь уче-

том в (53.7) только трех гармоник с n = 0, ±1 , сведем краевую задачу (53.8), (53.9) к сле-

дующей:

1 d

dφ−1

1 d

dφ0

−κ

−1

= 0,

−

= 0,

r dr

−1

r dr

1 d

dφ1

−κ φ

= −κ

P (r)

ω2 γ

−3

φ ,

r dr dr

1 1

1 b

(ω − ku − χu)2

(53.15)

φ−1 (r) +

φ−′′1 (r) +

K−1,0φ0′

(r)

= 0, φ1

(r) +

φ′′1 (r) +

K1,0φ0′(r)

= 0,

r=R

φ0 (r) +

φ0′′(r) +

(K0,−1φ−′1

(r) + K0, 1φ′1

(r))

= 0.

r=R

Задача (53.15) все еще слишком сложна. Поэтому ограничимся ее решением только в предельном случае электронного пучка малой плотности.

Если плотность пучка мала, то дисперсионное уравнение можно получить методом последовательных приближений. В нулевом приближении по плотности пучка (т.е. при

ωLb2 = 0 ) имеем решения (53.10). Подставляя их в граничные условия задачи (53.15), получа-

ем дисперсионное уравнение нулевого приближения (оно определяет частоты вакуумного гофрированного волновода):

2 2 ~	(53.16)
Dh (ω, k) ≡ J0 (iκ−1R)J0 (iκ0 R)J0 (iκ 1R) +κ0 h D(ω, k) = 0 ,

266

Александров А.Ф., Кузелев М.В. Физика электронных пучков

где D~(ω, k) ~1 – функция, явный вид которой не имеет для нас значения. В следующем при-

ближении

φ−1 (r) = A−1J0 (iκ−1r),

φ0 (r) = A0 J0 (iκ0r),

φ1 (r) = A1[J0 (iκ 1r) + Φ(r)],

(53.17)

а функция Φ(r)

удовлетворяет неоднородному уравнению

1 d

dΦ

−κ2Φ = −κ2 P (r)

ω2 γ −3

(iκ

r) .

(53.18)

r dr

(ω − ku − χu)2

1 b

Определяя ограниченное в нуле решение уравнения (53.18), получаем следующее выражение для собственной функции первого по плотности электронного пучка приближения:

			~
φ1 (r) = A1J0 (iκ 1r)[1− Φ(r)],
~	2 ωLb2 γ −3	r	′ 2	′	−1 r′		′′ ′′	2	′′ ′′ ′	(53.19)
Φ(r) = κ 1 ∆2		∫(r J0		(iκ 1r ))		∫r Pb (r )J0			(iκ 1r )dr dr	.
	1	0				0

Подставляя функцию (53.19) и первые две функции (53.17) в граничные условия зада-

чи (53.15) и исключая постоянные A0, ±1 , приходим к дисперсионному уравнению первого приближения

Dh (ω, k) +

′

~ ′

= 0 .

(53.20)

K0,1K1,0 J0 (iκ 1R)J0 (iκ−1R)J0

(iκ0 R)Φ (R)

Отбрасывая в выражении (53.16) для Dh (ω, k)

несущественные поправки, пропорциональные

h2κ02 , запишем дисперсионное уравнение (53.20) в более простом виде

−3

k mс

ωLbγ

− k

− k mс

(hχ)

Gbmω

1 −

(53.21)

(ω − ku − χu)

Здесь введено обозначение для геометрического фактора электронного пучка

Gbm =

∫0

rPb (r)I0

(xR)dr

, x =

(53.22)

R2 I02 (xR)

uγ

а I0 (xr) - функция Инфельда.

Будем искать решение уравнения (53.21) в виде ω = ω0 +δω ,

k = k0 +δk , где ω0 , k0 -

решение системы (53.14). В переменных δω и δk

уравнение (53.21) записывается следую-

щим образом:

−3

k m

(δω −δkVg )(δω −δku)

(hχ)

Gbm 1 −

ω0ωLbγ

(53.22)

где Vg = k0c2 ω0 - групповая скорость излучаемой волны. Легко видеть, что между уравнени-

ем (53.22) и дисперсионным уравнением (52.27) ондуляторного излучения имеется сходство - дисперсионное уравнение (53.22) описывает пучковую неустойчивость, обусловленную од-

267

Александров А.Ф., Кузелев М.В. Физика электронных пучков

ночастичным вынужденным излучением прямолинейного пучка электронов в гофрированном волноводе. Заметим, что в рамках теории возмущений по плотности пучка, использованной при получении уравнения (53.22), коллективный режим излучения описан быть не может.

Полагая в (53.22) δk = 0 , найдем максимальный инкремент неустойчивости, обусловленной одночастичным излучением в гофрированном волноводе (сравни с (52.29))

	−1 + i			3	1				2							2			2			2	−3 1 3
δω =	−1 + i			3	1	(hχ)			2					−	k mс							ωLbγ	ω0 .	(53.23)
δω =		2			4	(hχ)				Gbm 1				−	χ	2	2	γ		2		2	ω0 .	(53.23)
		2			4										χ		u	γ				ω0
Учитывая теперь связь Imω = b													3 2 и формулу (53.23), для общего параметра (45.13) имеем
	1		2						2			2			2		−3	1 3
b =	1	(hχ)	2				−	k mс						ωLbγ							ω0 .			(53.24)
b =	4	(hχ)		Gbm 1			−	χ	2	2	γ		2			2					ω0 .			(53.24)
	4							χ		u	γ				ω0

Подставляя далее (53.24) в общие условия (48.16) и (49.6), получим стартовые условия начала генерации в излучателях на прямолинейных электронных пучках в слабо гофрированных резонаторах на попутной и встречной волнах, работающих в одночастичном режиме

−3 1 3

3 u2 | V

| (2

3) ln 3 | κ κ

|−1, V

> 0,

(hχ)2 G

−

1 2

(53.25)

|),

< 0.

χ2u2γ 2

ω2

p(| κ κ

Возможен конечно и коллективный режим генерации в гофрированных системах. Однако рассмотрение его связано с громоздкими математическими выкладками и поэтому здесь не проводится.

§U 54. Мазеры на циклотронном резонансе

В постоянном однородном внешнем магнитном поле B0 электрон движется по закону

(см. (3.6) и (3.8))

rr	(t) = ρ	e	sin Ω	t er	+ ρ	e	cos Ω	t er	+ ut er	,
e	r&	e	e	x		e	e	y	z		(54.1)
r	r&						r		r	r	(54.1)
ve (t) = re (t) = u cos Ωet ex −u sin									Ωet ey	+ u ez ,

Здесь Ωe = ωe γ , ωe = eB0 mc - электронная циклотронная частота, ρe = u Ωe - ларморов-

ский радиус, γ = (1 − u2 c2 − u2 c2 )−1 2 - релятивистский фактор электрона, u и u - состав-

ляющие скорости поперек и вдоль магнитного поля, а erx , ery , erz - единичные орты декартовой системы координат (внешнее магнитное поле направлено вдоль оси Z ). Вычислим работу

W , совершаемую в единицу времени полем E ={Ex , Ey , 0} монохроматической поперечной циркулярно поляризованной электромагнитной волны

Ex + iEy = E0 exp[mi(ωt − kz)]

(54.2)

268

Александров А.Ф., Кузелев М.В. Физика электронных пучков

над электроном, движущимся по закону (54.1):

W (t) = evr

(t)E(t, rr)

r r

= eu

cos[(ω − ku m Ω

)t].

(54.3)

r =re (t )

Среднее за интервал времени

значение работы W определяется выражением (сравни с

(51.4))

1 t

sin ∆±t

W =

∫0 W (t′)dt′ = eu E0

(54.4)

∆±t

где ∆± = ω − ku m Ωe . При t → ∞ средняя работа (54.4) отлична от нуля только при выполне-

нии одного из резонансных условий ∆± = ω − ku m Ωe = 0 . Возникающее при этом излучение называется магнитно циклотронным. Соотношения (сравни с (51.7) и (51.8))

ω − ku m Ωe = 0,			(54.5)
D (ω, k) ≡ ω2	− k 2c2	−ω2
			= 0
w

определяют частоту магнитно циклотронного излучения электрона в волноводе. СВЧ приборы, основанные на магнитно циклотронном излучении, получили название мазеров на циклотронном резонансе – МЦР.

Движение электрона в магнитном поле, описываемое формулами (54.1), в отличие от (51.1) не является плоским. Поэтому теория магнитно циклотронного излучения оказывается более сложной, чем теория ондуляторного излучения, изложенная в § 52. Тем не менее при определенных условиях описание мазеров на циклотронном резонансе возможно в рамках моделей, рассмотренных в главе IX. Рассмотрим пучок электронов, движущихся по винтовым траекториям в однородном внешнем магнитном поле. Невозмущенную функцию рас-

пределения пучка по импульсам зададим в виде

(rr , p

, p ) =

(rr

)

n0b

δ( p

− p

)δ( p − p ) .

(54.6)

2πp 0

||0

Здесь

P (rr ) - функция, задающая поперечное к направлению магнитного поля распределе-

ние плотности электронов,

p и p|| - поперечная и продольная составляющие импульса элек-

трона,

p 0 = mu γ , p||0

= muγ , а u и u - величины, входящие в (54.1).

Электронный пучок с распределением (54.6) в электродинамике плазмы называют потоком моноэнергетических осцилляторов. Используем известное из электродинамики плазмы выражение для тензора диэлектрической проницаемости потока осцилляторов. Напомним, что тензор диэлектрической проницаемости полностью описывает электромагнитные свойства любой плазмаподобной среды в линейном приближении. В цилиндрической систе-

ме координат ( rr ={r, ϕ}, rr ={r, ϕ, z} ) тензор диэлектрической проницаемости потока ос-

цилляторов является оператором и определяется следующими формулами: 269

ε(+)

ε(−)

ε|(| +)

ε|(| −)

= − ωLb2 γ −1

2ω2

= − ωLb2 γ −1

2ω2

= ω2

ωLb ω

2 2

= ω2

ωLb ω

2 2

Александров А.Ф., Кузелев М.В. Физика электронных пучков

ω − ku

1 u2 (k 2 −ω2 c2 )

ω − ku − Ω

2 (ω − ku − Ω

ω − ku

1 u2 (k 2 −ω2 c2 )

ω − ku + Ω

2 (ω − ku + Ω

+ u 2

(ω − Ωe )

−ω

u ωe

−1

− ku − Ωe

(ω − ku − Ωe )

−1

ωe

+ u 2

(ω + Ωe )

−ω

− ku + Ωe

(ω − ku + Ωe )

εb = ε(+) +ε(−) ,

gb = ε(+) −ε(−) ,

ε|b| = ε|(|+) −ε|(|−) ,

= ε

ϕϕ

=1 +εb P (r),

rϕ

= −ε

ϕr

= −igb P

(r),

= −

ugb

P (r)

ϕz

ω − ku b

ugb

1 d

rP (r),

ω − ku r dr

zϕ

= −i

γu

gb P (r)

ωe

= −i

γu

rP (r),

ωe

r dr

=1 −

ω2

γ −3

+εb

1 d

(r)

(ω − ku)2

| |

r dr b

(54.7а)

(54.7б)

(54.7в)

При помощи тензора диэлектрической проницаемости вычисляются компоненты вектора

индукции электрического поля D : например, Dϕ = εrr Er +εrϕ Eϕ +εrz Ez .

Полная система уравнений Максвелла для возмущений f (r) exp(−iωt + ikz + ilϕ) в

среде с тензором диэлектрической проницаемости (54.7в) имеет вид:

(1)i rl Ez −ikz Eϕ = i ωc Br ,

(2)ikz Er − dEdrz = i ωc Bϕ ,

(3)

1 d

(rE

)−i

= i

ω B

r dr

(54.8)

ω ε

(4)

− ik

B = −i

−i

z ϕ

rϕ ϕ

(5)ikz Br − dBdrz = −i ωc εϕr Er −i ωc εϕϕ Eϕ − i ωc εϕz Ez ,

(6)1r drd (rBϕ )−i rl Br = −i ωc εzr Er − i ωc εzϕ Eϕ − i ωc εzz Ez .

Если система (54.8) решается в круглом волноводе с радиусом R , то должны использоваться

270

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2627 / 2927 28 29 > Следующая >>>

Соседние файлы в папке ЭЛТ

#
29.03.20164.53 Mб3427_VaN[1].pdf
#
29.03.2016116.12 Кб20Мониторы с ЭЛТ лекция.mht
#
29.03.20166.45 Кб22Схема монитора с ЭЛТ.gif
#
29.03.201634.05 Кб21Устройство кинескопа.jpg
#
29.03.2016133.55 Кб21Устройство монитора на ЭЛТ.jpg
#
29.03.201622.05 Кб22Устройство ЭЛТ.gif