Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

Аппаратные средства вычислительной техники

Файл:

27_VaN[1]

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

4.53 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 295 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Александров А.Ф., Кузелев М.В. Физика электронных пучков

электронно-оптическом изображении. Ее называют линейным увеличением. Кроме (10.6)

имеет место еще одно соотношение
r′(a) = c1 ,	r′(b) = c1r1′(b) .		(10.8)
Поскольку (см. Рис. 10.2) tgα ≈α = c1,		′
Поскольку (см. Рис. 10.2) tgα ≈α = c1,		tgβ ≈ β = c1r1	(b) , то величина
β	′		(10.9)
K = α = r1 (b)			(10.9)

характеризует изменение угла раствора пучка электронов при переходе от объекта к изображению. Ее называют угловым увеличением.

Найдем связь между линейным и угловым увеличениями. Из теории дифференциаль-

ных уравнений вида (10.2) известно следующее соотношение:
′	′				C	,	(10.10)
r1 (z)r2 (z)	− r1	(z)r2 (z) =			ϕ0 (z)

где C - постоянная. Выражение в левой части (10.10) называется определителем Вронского
функций r1,2 (z) . Полагая в (10.10)						z = a и учитывая условия (10.3), найдем	C = − ϕ0 (a) .
Подставляя далее в (10.10) z = b и учитывая, что r1 (b) = 0 , получим равенство
′	=	ϕ0	(a)	.			(10.11)
r1 (b)r2 (b)		ϕ0	(b)

Из (10.11) следует искомое соотношение между линейным и угловым и угловым увеличениями

K Kl =	ϕ0	(a)	.	(10.12)
	ϕ0	(b)

Пусть la и lb - линейные размеры объекта и его изображения соответственно, а a и

b - углы растворов конусов лучей, выходящих из некоторой точки объекта и сходящихся в сопряженной точке изображения. Очевидно, что в параксиальном приближении можно записать

K	l	=	lb	, K	=	b .	(10.13)

			la			a
Подставляя (10.13) в (10.12), получим важное соотношение
la a			ϕ0 (a) = lb b ϕ0 (b) .				(10.14)
В обычной оптике световых пучков аналог соотношения (10.14) la a n(a) = lb b n(b)							известен

как теорема Лагранжа-Гельмгольца.

Получим теперь непосредственно из уравнения (10.2) формулу тонкой электростатической линзы и выражение для ее фокусного расстояния. Для простоты рассмотрим линзу, в

Александров А.Ф., Кузелев М.В. Физика электронных пучков

которой потенциал одинаков с обеих сторон от оптического центра (по Рис. 8.1 левее точки “А” и правее точки “В”). Такие линзы называются не иммерсионными. Не иммерсионную линзу можно изготовить при помощи трех цилиндров (или трех диафрагм), крайние из которых должны находиться под одинаковым потенциалом.

Здесь опять будет полезен Рис. 8.1. Потенциал вне линзы обозначим через ϕ00 . Элек-

тронные траектории выходят из точки “Р” (она расположена в плоскости объекта z = a ) и собираются в сопряженной точке “Р'” (плоскость изображения z = b ). Проинтегрируем уравнение (10.2а) от a до b . Получим

dr(b)

−

dr(a)

= −

ϕ0′′(z)

dz .

(10.15)

r(z)

ϕ0 (z)

4 ∫a

Поскольку линза является тонкой, то r(z) под интегралом в (10.15) можно заменить на r(0) .

С той же точностью (с учетом знаков)

dr(a)

= −

r(0)

dr(b)

= −

r(0)

(10.16)

ξ′

Подставляя (10.16) в (10.15) и вводя обозначения

∂2ϕ

′

f = 4

dz,

= − f

(10.17)

∫

∂z2

r=0

перепишем соотношение (10.15) в виде формулы тонкой линзы (8.21). Легко видеть, что выражениями (9.16) для фокусных расстояний электростатической линзы, полученные по ана-

логии с лучевой оптикой, при ϕ 1 =ϕ 2 =ϕ00 сводятся к формулам (10.17).

Очевидно, обобщение проведенного рассмотрения на случай иммерсионной линзы. В этом случае при интегрировании уравнения (10.2) вместо (10.15) получим следующее соотношение:

dr(b)		dr(a)		1	b	ϕ0′′(z)
ϕ02 dz	− ϕ01	dz	= −	4	∫a r(z)	ϕ0 (z)	dz ,	(10.18)

где ϕ01 и ϕ02 потенциалы на главной оптической оси в плоскости объекта и изображения со-

ответственно. У иммерсионной электростатической линзы по определению ϕ01 ≠ ϕ02 . В пара-

ксиальном приближении из (10.18) легко могут быть получены формулы (9.16).

§11. Фокусировка электронных пучков постоянным магнитным полем

Воднородном постоянном магнитном поле движение заряженной частицы складывается из движения по окружности поперек магнитного поля и равномерного прямолинейного

движения вдоль поля. В результате траекторией частицы является винтовая линия. Если v и

Александров А.Ф., Кузелев М.В. Физика электронных пучков

v|| компоненты скорости электрона поперек и вдоль вектора магнитного поля Br0 , то радиус

орбиты кругового движения есть ρe = v Ωe , Ωe = eB0									mc - электронная циклотронная час-
тота, а шаг винтовой линии определяется формулой
h		= v T	= v	2π		= 2π	mc	v cos β .	(11.1)
							eB
	e	\|\| e	\|\| Ω		e			0
						0
Здесь v	0	= v2	+ v2 - полная скорость электрона, которая в постоянном магнитном поле по-
			\|\|
стоянна,		а β - угол между направлениями начальной скорости и магнитного поля. Поясним,

что здесь мы ограничиваемся рассмотрением нерелятивистского движения. Кроме того, все сказанное очевидно относится не только к электрону, но и к любой заряженной частице при замене e → eα , m → mα , где α - сорт частицы.

Предположим, что электронный пучок с малой угловой расходимостью 2∆β выходит из некоторой точки “O” под средним углом β0 , т.е. в формуле (11.1) β (β0 − ∆β, β0 + ∆β) .

Поскольку траектории электронов винтовые линии, то через интервал времени Te = 2πΩe

они пересекут силовую линию магнитного поля, проходящую через точку “O”. Однако пере-

секут указанную линию они не в одной точки, а в области x (x0 − ∆x, x0 + ∆x) , где

= 2π

cos β

, ∆x = 2π

sin β

∆β ,

(11.2)

причем координата

x отсчитывается от точки “O” вдоль силовой линии в направлении по-

ступательного движения электрона.

При β0

= 0 имеем и ∆x = 0 . Следовательно, электронные траектории, выходящие из

точки “O” на силовой линии магнитного поля, собираются в точке “O1” на той же силовой линии. Расстояние между точками “O” и “O1” дается величиной x0 из (11.2) (при cos β0 →1 ).

Таким образом, имеет место продольная фокусировка параксиального ( ∆β <<1) электронно-

го пучка однородным магнитным полем. При увеличении среднего угла β0 фокусировка ухудшается. Продольная фокусировка может быть использована для получения электроннооптического изображения. Если в плоскости перпендикулярной к магнитному полю поместить объект, каждая точка которого испускает электронный пучок с малой угловой расходи-

мостью, то на расстоянии x0 сформируется прямое изображение объекта с увеличением,

равным единице.

Рассмотрим теперь поперечную фокусировку электронов в однородном магнитном поле. Пусть электрон со скоростью v0 = v вылетает из точки “A” оси x вдоль оси y , а маг-

нитное поле направлено параллельно оси z. Совершив в магнитном поле половину оборота

Александров А.Ф., Кузелев М.В. Физика электронных пучков

по ларморовской окружности электрон возвратится к оси x в точке “B”, отстоящей от “A” на расстоянии 2ρe . Рассмотрим еще один электрон, вылетающий из точки “A”, тоже в плоско-

сти xy , но под углом δ к первому электрону. Элементарный тригонометрический расчет по-

казывает, что второй электрон пересечет ось x в точке, отстоящей от “B” на расстоянии

∆ = 4ρ	e	sin2 δ ≈ ρ δ 2 .		(11.3)
	e	2	e
		2

Если теперь рассмотреть пучок электронов, вылетающих из точки “A” с угловой расходимостью в пределах ±δ , то окажется, что около точки “B” этот пучок сходится в области с размером (11.3). Это и есть поперечная фокусировка электронного пучка в однородном магнитном поле.

Поперечная магнитная фокусировка находит широкое применение в приложениях (например, в масс-спектроскопии и электромагнитном разделении изотопов). Дело в том, что

ларморовский радиус частиц сорта α
ρα	=	mα		v c	,	(11.4)
		e		B
		α	0

определяющий положение и размер области фокусировки зависит от отношения массы частицы к ее заряду. Поэтому ионы разного сорта фокусируются в разных точках оси x , где они и улавливаются соответствующими приемниками. Но этот вопрос, как не относящийся к физике электронных пучков, здесь не рассматривается.

Применительно к электронным пучкам ни продольная ни поперечная фокусировки в однородном магнитном поле существенного практического значения не имеют. А вот фокусировка электронных пучков с помощью магнитостатических линз оказалась чрезвычайно важной для современной экспериментальной физики. Магнитной линзой может быть короткий соленоид – короткая магнитная катушка, по обмотке которой протекает постоянный азимутальный ток. Такой соленоид создает аксиально-симметричное магнитное поле с от-

личными от нуля компонентами магнитной индукции Br (r, z) и Bz (r, z) , а азимутальная компонента магнитной индукции Bϕ в соленоиде равна нулю. Здесь r, ϕ, z - цилиндрические координаты, которые следует использовать при описании движения электрона в аксиальносимметричном магнитном поле. Ось цилиндрической системы координат является осью симметрии магнитного поля и совпадает с осью соленоида.

Фокусирующее действие аксиально-симметричного магнитного поля можно пояснить с помощью Рис. 11.1. На рисунке в плоскости, проходящей через ось симметрии z, изображены сечение соленоида, две силовые линии магнитного поля – тонкий пунктир и две характерные траектории электронов – жирный пунктир. Электроны, влетающие слева параллельно

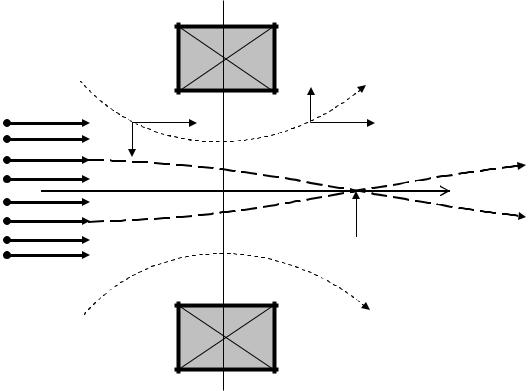
Александров А.Ф., Кузелев М.В. Физика электронных пучков

		Br	B
e	v	Bz	Bz
		Br
			z
			B
		z = 0

Рис. 11.1

К пояснению фокусирующего действия магнитной линзы

Александров А.Ф., Кузелев М.В. Физика электронных пучков

оси, показаны стрелками. Определяющим для фокусирующего действия магнитного поля соленоида является азимутальное движение электрона, которое возникает под действием со-

ставляющей силы Fϕ = e(vz 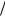c)Br . Если Br направлена так, как изображено на рисунке, то в области z < 0 в верхней части соленоида компонента скорости электрона vϕ направлена к

читателю, а в нижней части – от него ( e < 0 ). При этом компонента силы Fr = e(vϕ 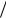c)Bz на-

правлена к оси системы. Именно Fr производит фокусировку. Вплоть до плоскости z = 0

компонента скорости vϕ нарастает, растет и Bz (см. Рис. 11.2), т.е. эффект фокусировки уси-

ливается. В области z > 0 направление Br изменяется на противоположное. Фокусировка,

однако, продолжается, поскольку знаки vϕ и Bz не меняются. В результате прохождения

электрона через линзу его траектория повернется на некоторый угол вокруг оси симметрии линзы и пересечет эту ось в некоторой точке (возможно даже несколько последовательных пересечений). Так как траектория электрона поворачивается, то на Рис. 11.1 изображены на самом деле не траектории, а геометрические места точек пересечения траекторий с плоскостью рисунка. Точка фокуса отмечена на рисунке стрелкой. Легко видеть, что результат нашего качественного рассмотрения сохранится, если направления магнитного поля соленоида поменять на противоположное.

Отметим особенности магнитных линз как фокусирующих элементов электроннооптических систем. Во-первых, фокусировка в магнитном поле неизбежно сопровождается поворотом изображения. Во-вторых, поле магнитной линзы всегда собирает электронный пучок, т.е. рассеивающих магнитных линз не существует.

Перейдем к вычислению фокусного расстояния магнитной линзы с аксиальносимметричным магнитным полем. В параксиальном приближении можно положить

	Bz (r, z) ≈ Bz (0, z) ≡ Bz0 (z) .							(11.5)
Запишем, с учетом (11.5), уравнение div B = 0 в цилиндрической системе координат
	1		∂	(rB ) +		dBz0	= 0 .	(11.6)
				(rB ) +			= 0 .	(11.6)
	r ∂r			r		dz
	r ∂r					dz
Будем искать Br					в виде
	B = a(z)rn ,							(11.7)
		r

где n - постоянная, а a(z) - функция только z. Подставляя данное представление в (11.6), по-

лучим уравнение для a(z)

(n +1)rn−1a(z) +	dBz0	= 0 .	(11.8)
(n +1)rn−1a(z) +	dz	= 0 .	(11.8)
	dz
Из (11.8) видно, что следует положить n =1, иначе функция a(z)			будет зависеть еще и от r.
		46

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Отсюда и из (11.7) находим выражение для компоненты Br (r, z)

в параксиальном приближе-

нии

B (r, z) = −

dBz0

(11.9)

Запишем теперь уравнение движения электрона в цилиндрических координатах в

магнитном поле с ненулевыми компонентами Br , Bz и Bϕ = 0

d 2 z

dϕ

B ,

dt2

d 2r

dϕ

− r

= −

(11.10)

dt2

dϕ

r(vz Br − vr Bz ).

= −

Используя соотношение (11.9), преобразуем последнее уравнение в (11.10) к виду

dϕ

dBz0 dz

e d

Bz0 ).

+ r

Bz0 =

(11.11)

2mc dt

Интегрирование уравнения (11.11) дает следующее выражение для угловой скорости вращения электрона:

dϕ	=	e	B	z0	(z) ,	(11.12)
dt		2mc

где z = z(t) - продольная координата электрона. При получении (11.12) полагалось, что при z → −∞ магнитное поле равно нулю и вращение у электрона отсутствует.

В параксиальном приближении можно записать

dϕ

= v

dϕ

≈ v

dϕ

(11.13)

dz dt

z dz

где v - полная скорость электрона,

которая в постоянном магнитном поле неизменна. Из

(11.13) находим выражение для угла поворота траектории, т.е. изображения, в плоскости z = z0

	e	z0
ϕ(z0 ) =		Bz0 (z)dz .	(11.14)
	2mvc
		−∫∞

Подставляя (11.14) во второе уравнение (11.10) и переходя от дифференцирования по t к

дифференцированию по z (в параксиальном приближении dt = dz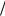v ), после простых преобразований получим следующее уравнение:

d 2r(z)		1			e	2	2
	= −					B	z0	(z)r(z) .	(11.15)
dz2		4v	2
				mc

Уравнения (11.14) и (11.15) полностью описывают формирование электронно-оптических

Александров А.Ф., Кузелев М.В. Физика электронных пучков

изображений с помощью аксиально-симметричного магнитного поля магнитной линзы. Уравнение (11.15) является аналогом уравнения (10.2) электростатической линзы. Фокусирующее действие магнитной линзы, в отличие от линзы электростатической, разное для зараженных частиц разного сорта, поскольку зависит от отношения заряда к массе.

Интегрируя уравнение (11.15) по z от плоскости объекта ( z = a ) до плоскости изображения ( z = b ) в приближении тонкой линзы, получим формулу (8.21), в которой фокусные расстояния определяются формулами (сравни с (10.17))

1		1		e 2 b			2
	=				∫a	B	z0	(z)dz, f ′ = − f .	(11.16)
		4v2
f			mc

Из общего курса физики известно, что индукция магнитного поля на оси соленоида длины L

и радиуса R на расстоянии L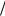2 от его концов (т.е. в точке z = 0 ) максимальна и вычисляет-

ся по формуле

			4π	NI			R	2	−1
Bz0
	(0)	=			1	+ 4			.	(11.17)
			c	L			2
							L
Здесь N -	полное число витков соленоида,									I - сила тока в витке. Если 2R < L (длинный со-

леноид), то вне соленоида магнитное поле мало и интегрирование в (11.16) достаточно проводить по внутренней области соленоида. Тогда для фокусного расстояния длинного соленоида из (11.16) и (11.17) имеем следующую оценку:

f =	1	L	v2	I	0	2
						,	(11.18)
	4π 2		c2
				NI

где I0 = mc3e - величина размерности тока, численно равная 17 103 A . Таким образом фо-

кусное расстояние тонкой магнитной линзы на основе длинного соленоида пропорционально его длине L и обратно пропорционально квадрату числа ампер-витков NI .

Рассмотрим теперь противоположный случай короткого соленоида. Более того, пе-

рейдем к пределу LR → 0 . В этом случае вместо приближенной оценки проще получить точную формулу. Используем известную из общего курса формулу для индукции магнитного поля на оси бесконечно тонкого кольцевого тока с силой NI (все витки соленоида собраны в точку)

		2π	NI			z	2		−3 2
Bz0	(z) =				+					(11.19)
		c	R	1		R		2	.

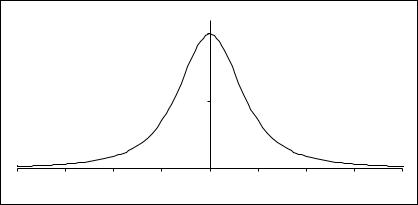
Зависимость (11.19), типичная для тонких магнитных линз, представлена на Рис. 11.2. Подстановка (11.19) в (11.16) дает следующий результат:

Александров А.Ф., Кузелев М.В. Физика электронных пучков

				1	Bz 0(z )/Bz 0(0)
				1
				0.5
				0				z/R
				0
-4	-3	-2	-1	0	1	2	3	4

Рис. 11.2

Продольная составляющая индукции магнитного поля короткого соленоида

				Александров А.Ф., Кузелев М.В. Физика электронных пучков
f =	8	R	v2		I	0	2
							.	(11.20)
	3π 3		c2
					NI

Следовательно фокусное расстояние тонкой магнитной линзы на основе короткого соленоида пропорционально его радиусу R и обратно пропорционально квадрату числа ампервитков NI . Фокусное расстояние, определяемое формулой (11.20), является минимально возможным. Поскольку уменьшать длину соленоида с большим числом ампер-витков NI сколь угодно сильно нельзя, то применяют бронирование катушки железным панцирем с узким кольцевым зазором с внутренней стороны соленоида. Короткофокусные магнитные линзы дают большое увеличение и применяются в электронной микроскопии.

§ 12. Электронный микроскоп

Самым важным практическим результатом геометрической электронной оптики является создание электронного микроскопа. Ход лучей в электронном микроскопе, предназначенном для получения изображения тонкого объекта в проходящих электронных лучах, такой же, как в аналогичном оптическом микроскопе (Рис. 12.1). Разница заключается в том, каким образом возникает контраст между различными частями изображения. В оптическом микроскопе контраст обусловлен различным поглощением световых лучей в разных частях объекта. Электроны в объекте не поглощаются (в противном случае объект бы просто разрушился), но рассеиваются. Причем участки объекта с большей плотностью или толщиной рассеивают электроны сильнее, т.е. отклоняют их на больший угол. Различие в степени рассеяния электронов различными частями объекта и используется для формирования контрастного изображения в электронной микроскопии. Если изображение получается при помощи электронных лучей отклоненных в объекте на малые углы, то оно называется светлопольным. Изображение может быть сформировано и при помощи лучей рассеянных на большие углы, а электроны с малыми углами отклонения к плоскости изображения с помощью какихто приспособлений не пропускаются. В этом случае изображение называется темнопольным.

Рис. 12.1 иллюстрирует формирование светлопольного изображения. Электронный пучок созданный источником фокусируется конденсорной линзой на объект А0В0. Объектив формирует промежуточное, увеличенное, действительное изображение объекта А1В1. Проекционная линза дает окончательное изображение А2В2 на фото пластинке или флюоресцирующем экране.

Основными характеристиками микроскопа являются увеличение и разрешающая способность. Увеличение определяется совместным увеличением объектива и проекционной линзы. Причем увеличение тем больше, чем меньше фокусные расстояния линз. Из формул (9.16), (9.17), (11.16), (11.18) и (11.20) видно, что электростатические и магнитостатические

<<< < Предыдущая 1 2 3 45 / 295 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке ЭЛТ

#
29.03.20164.53 Mб3427_VaN[1].pdf
#
29.03.2016116.12 Кб20Мониторы с ЭЛТ лекция.mht
#
29.03.20166.45 Кб22Схема монитора с ЭЛТ.gif
#
29.03.201634.05 Кб21Устройство кинескопа.jpg
#
29.03.2016133.55 Кб21Устройство монитора на ЭЛТ.jpg
#
29.03.201622.05 Кб22Устройство ЭЛТ.gif