|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
d |
jei = −(1 |
|
+ |
1 |
(1 |
1 |
i∑ |
1 |
|
(38.30) |
dτ |
+ m M ) 1 |
λ |
2 |
+ m M ) |
n |
(ρen ρin − к.с) . |
|
|
|
|
|
4 |
n |
|
|
В силу неравенства (38.28) уравнение (38.30) практически не отличается от полученного в потенциальном приближении уравнения (38.25). Следовательно, при выполнении неравенства (38.28) постоянная составляющая тока в плазме изменяется почти так же, как в потенциальном случае.
Рассмотрим теперь предел, противоположный (38.28). В этом случае из третьего урав-
нения системы (38.21) имеем |
|
|
|
|
|
|
|
|
|
|
|
dB |
|
= jei −1 . |
|
|
|
|
|
|
|
|
|
(38.31) |
|
dτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (38.31) и (38.25) следует, что |
|
|
|
|
|
|
|
|
|
|
d 2 |
|
|
1 |
|
d |
|
1 |
|
|
|
|
2 |
+ (1 + m M ) ( jei −1)= −(1 |
+ m M ) |
|
i |
|
∑ |
|
(ρen ρin − к.с) . |
(38.32) |
4 |
|
n |
dτ |
|
|
|
|
dτ |
n |
|
|
|
Уравнение (38.32) совершенно не похоже на (38.30). Левая часть этого уравнения описывает волны постоянного тока (с kz = k = 0 ) в безграничной электрон-ионной плазме со спектром волн
ω2 = (1+ m M )ωLe2 . |
(38.33) |
Правая часть уравнения (38.32) изменяется за времена, определяемые инкрементом (38.11), что значительно меньше частоты (38.33). Поэтому из (38.32) для тока получаем следующее выражение:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
d |
|
1 |
|
|
|
jei =1− |
|
i |
|
∑ |
|
(ρen ρin − к.с) . |
(38.34) |
4 |
|
n |
|
|
dτ |
n |
|
|
|
Выше говорилось, что при резонансной неустойчивости Бунемана ионы плазмы могут описываться в линейном приближении, а значит безразмерные амплитуды гармоник возмущения плотности ионов малы, т.е. | ρin |<<1. Поскольку | ρen | ~ 1(*) (см. Рис. 38.2), то из (38.34) име-
ем оценку jei ~ 1.
Таким образом величина параметра (38.24) существенно определяет динамику постоянной составляющей тока в плазме при бунемановской неустойчивости. Следует ожидать,
что при λ 2 >>1 должно наблюдаться значительное уменьшение тока, а при λ 2 <<1 срыва тока в плазме нет. На Рис. 38.4 представлены результаты численного решения уравнений
(38.21) при различных значениях параметра λ 2 , полностью подтверждающие сказанное вы-
ше. Заметим, что кривая тока с Рис. 38.2 соответствует случаю λ 2 = ∞.
(*) Размерные амплитуды гармоник возмущений плотности определяются формулами n0i ρin , n0e ρen .
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Рис. 38.4
Динамика тока при бунемановской неустойчивости в квазиодномерной системе с учетом непотенциальных эффектов: 1 - λ 2 = 0.1 ; 2 - λ 2 =1; 3 - λ 2 = 5
Александров А.Ф., Кузелев М.В. Физика электронных пучков
§ 39. Общая классификация пучковых неустойчивостей
Чтобы дать универсальную классификацию пучковых неустойчивостей и родственных им явлений запишем классическое дисперсионное уравнение (32.4) в виде
(ω2 −ωLe2 )((ω − kzu)2 −ωLb2 γ −3 )= ωLe2 ωLb2 γ −3 . |
(39.1) |
Первая скобка в левой части описывает собственные колебания холодной безграничной плазмы: ω2 = ωLe2 . Вторая скобка описывает собственные волны пучка (см. спектры (27.7)): (ω − kzu)2 = ωLb2 γ −3 . Правая часть в (39.1) задает связь двух колебательных систем – плазмы и пучка. Оказывается, что структура типа (39.1) свойственна большинству систем, в которых развиваются пучковые неустойчивости, связанные с вынужденным излучением волн произвольной природы.
Перепишем дисперсионное уравнение (39.1) в универсальной обобщенной форме
(ω2 − Ω2Le ) ((ω − kzu)2 − Ω2Lb )= ΘΩ2LeΩ2Lb . |
(39.2) |
Величины Ω2Le и Ω2Lb , очевидно, имеют смысл квадратов частот собственных колебаний плазмы (или какой-то другой среды) и пучка соответственно. В общем случае выражения
ω = ΩLe и ω = kzu ± ΩLb нельзя рассматривать как явное задание спектров собственных коле-
баний. Это – неявные формы спектров, поскольку ΩLe и ΩLb зависят, вообще говоря, от kz и
ω . Тем не менее, запись (39.2) оказывается весьма полезной и эффективной. Уравнение (39.1) имеет вид (39.2) при Θ =1, Ω2Le = ωLe2 , Ω2Lb = ωLb2 γ −3 . Параметр Θ будем называть коэффициентом связи волн (колебательных систем).
Для выяснения сути вопроса без усложняющих подробностей рассмотрим дисперси-
онное уравнение (39.2) в предположении, что величины Ω2Le , Ω2Lb и Θ являются постоянны-
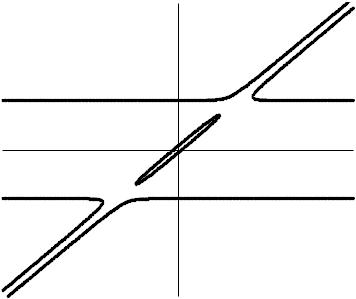
ми. На Рис. 39.1 изображены дисперсионные кривые уравнения (39.2), построенные для слу-
чая Θ = 0,5 и того же отношения ΩLb 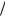 ΩLe , что взято при построении дисперсионных кри-
ΩLe , что взято при построении дисперсионных кри-
вых, приведенных на Рис. 32.1. Видно, что уменьшение Θ от единицы до 0,5 привело к значительному изменению топологии дисперсионных кривых. Так, непрерывная зона неустойчивости меду метками «1» и «2» (Рис. 32.1) разбилась на две довольно узкие зоны неустойчивости между метками «1» – «1*» и «2*» – «2» (Рис. 39.1). При дальнейшем уменьшении коэффициента связи Θ зона неустойчивости сужается: метки «1» и «2» остаются примерно на прежнем месте, а метки «1*» и «2*» удаляются от центра kz = 0 . Таким образом, при умень-
шении коэффициента связи пропадает нерезонансная апериодическая неустойчивость. Резонансная же неустойчивость остается, сосредоточиваясь во все более узкой зоне волновых чисел. Чуть ниже мы выясним, что при этом меняется и физический механизм резонансной не-
193
Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
|
ω |
|
|
ωLe |
|
|
|
|
1 |
1* |
2* |
2 |
kz |
l |
l |
l |
l |
|
|
|
|
|
-ωLe |
|
|
Рис. 39.1 |
|
|
Дисперсионные кривые уравнения (39.2) |
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков
устойчивости.
Факт исчезновения при малых Θ апериодической неустойчивости представляется достаточно понятным. Действительно, апериодическая неустойчивость имеет место, если электростатические силы, возникающие при нарушении квазинейтральности пучка, меняют знак. Это возможно только, если диэлектрическая проницаемость среды, в которой распространяется пучок, отрицательна. Уравнение (39.2) можно переписать в виде (см. (32.12))
|
Ω2 |
γ −3 |
|
|
Ω2 |
|
− (1 |
− Θ) |
Ω2 |
−1 |
|
|
|
Lb |
|
|
|
|
|
Le |
|
Le |
|
|
εэфф. − |
|
2 = 0 , |
− |
|
|
, |
(39.3) |
|
εэфф. = 1 |
ω |
2 |
1 |
ω |
2 |
|
|
(ω − kzu) |
|
|
|
|
|
|
|
|
|
|
где εэфф. - эффективная диэлектрическая проницаемость системы, в которой движется пучок.
Легко показать, что εэфф. |
< 0 |
в области |
|
ω=kzu |
|
|
|
(1 − Θ)Ω2Le < kz2u2 < Ω2Le . |
(39.4) |
При Θ → 0 нижняя граница этой области стремится к ΩLe , а ширина обращается в нуль.
Рассмотрим теперь, что происходит при уменьшении коэффициента связи с резонансной неустойчивостью. При Θ = 0 уравнение (39.2) распадается на два уравнения
|
ω2 |
= Ω2Le , |
(39.5) |
|
(ω |
− kzu)2 |
|
= Ω2Lb . |
Первое уравнение определяет спектр волн среды, второе – спектры пучковых волн: быстрой
и медленной. Совместное решение этих уравнений определяет на плоскости |
(ω, kz ) точки |
резонанса волн. Будем искать около резонансных точек решение уравнения (39.2) в виде |
ω = ΩLe +δω = kzu ± ΩLb +δω, |
(39.6) |
где верхний знак относится к резонансу между волной среды и быстрой пучковой волной, а нижний – к резонансу между волной среды и медленной волной пучка. Считаем также, что выполнено неравенство
означающее, что плотность пучка мала (см. (32.5)). Подставляя с учетом (39.7) выражения (39.6) в уравнение (39.2), преобразуем его к виду
|
|
|
|
|
|
|
δω(δω2 ± 2ΩLbδω)= |
1 |
ΘΩ2LbΩLe . |
(39.8) |
|
2 |
|
|
Проанализируем (39.8) в двух противоположных характерных предельных случаях. |
|
I. Предположим, что выполнено неравенство |
|
|
δω |
|
>> 2ΩLb . |
(39.9) |
|
|
При этом (39.8) сводится к кубическому уравнению, из которого следует комплексный инкремент

Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
−1 + i |
3 |
|
|
2 1 3 |
|
|
δω = |
|
Θ |
ΩLb |
ΩLe . |
(39.10) |
2 |
|
|
2 |
|
|
|
|
2ΩLe |
|
|
При Θ =1 инкремент (39.10) полностью совпадает (с точностью до обозначений) с инкрементом (32.11) резонансной неустойчивости безграничных пучка и плазмы. Резонансную пучковую неустойчивость с инкрементом типа (39.10) называют одночастичным вынужденным эффектом Черенкова. Подставляя (39.10) в (39.9), находим условие применимости инкремента (39.10)
В силу предположения (39.7) последнее неравенство выполняется только при достаточно больших коэффициентах связи. Например, оно выполнено для взаимопроникающих пучка и плазмы, когда Θ =1.
Неравенство (39.9) означает, что за время развития неустойчивости τ =δω−1 собственные волны пучка не успевают развиться. Следовательно, пучок ведет себя как набор отдельных частиц в поле волны в среде. Отсюда и название данной неустойчивости – одночас-
|
|
|
|
|
|
|
тичный вынужденный эффект Черенкова. |
|
II. Предположим теперь, что выполнено неравенство обратное (39.9) |
|
|
δω |
|
<< 2ΩLb . |
(39.12) |
|
|
При этом уравнение (39.8) сводится к следующему квадратному уравнению |
|
±δω2 = |
1 |
ΘΩLbΩLe , |
(39.13) |
|
4 |
|
|
в котором знак плюс следует брать при резонансе волны среды и быстрой волны пучка, а знак минус выбирается при резонансе волны среды и медленной пучковой волны. Видно, что неустойчивость имеет место только при резонансе с медленной волной электронного пучка, что обусловлено отрицательностью энергии последней. Из (39.13) при выборе знака минус следует инкремент
|
1 |
|
|
1 2 |
|
|
δω = |
|
Θ |
ΩLb |
ΩLe . |
(39.14) |
2 |
i |
|
|
|
|
ΩLe |
|
|
Этот инкремент по структуре качественно отличается от инкремента (4.1.11). Он характеризует иную резонансную неустойчивость - коллективный вынужденный эффект Черенкова. Подставляя (39.14) в (39.12), находим условие применимости инкремента (39.14)
Θ<<16 ΩLb . (39.15)
ΩLe
Всилу предположения (39.7) последнее неравенство выполняется только при малых коэф-

Александров А.Ф., Кузелев М.В. Физика электронных пучков
фициентах связи Θ .
Неравенство (39.12) означает, что за время развития неустойчивости τ =δω−1 элек-
троны пучка совершают много колебаний с частотой собственного волнового движения ΩLb .
Следовательно, пучок ведет себя как коллектив частиц, связанных единым волновым движением в собственном высокочастотном поле (плюс поле волны в среде). Отсюда и название данной неустойчивости – коллективный вынужденный эффект Черенкова. Заметим, что го-
воря о частоте собственных колебаний пучка мы взяли ΩLb без учета слагаемого kzu . Это так, поскольку частота kzu связана только с поступательным движением и описывает допле-
ровский сдвиг, к колебаниям отношения не имеющий.
Весьма полезной может быть следующая терминология и интерпретация рассмотренных процессов. Уравнение (39.2) можно трактовать как математическую структуру, описы-
вающую систему из двух связанных осцилляторов: один с частотой ΩLe , другой с частотой
ΩLb . Неустойчивость возникает при взаимодействии данных осцилляторов, поскольку знаки энергий у них различные. При одночастичном эффекте Черенкова взаимодействие столь сильное и быстрое, что осциллятор с частотой ΩLb не успевает совершить ни одного колеба-
ния. При коллективном эффекте взаимодействие слабое и на частоте ΩLb совершается много колебаний. В любом случае осциллятор с частотой ΩLe возбуждается, поскольку в силу ус-
ловия (39.7) выполнено неравенство δω << ΩLe . Последнее означает, что неустойчивость и при одночастичном и при коллективном эффектах приводит к возбуждению (излучению) волн среды (системы), в которой распространяется пучок.
Обсудим теперь в свете сделанной классификации резонансную неустойчивость Бу-
немана. Переписывая дисперсионное уравнение (38.2) в виде |
|
(ω2 −ωLi2 )((ω − kzu)2 −ωLe2 )= ωLi2 ωLe2 |
, |
(39.16) |
делаем вывод, что (39.16) описывает |
две связанные колебательные |
системы – ионную |
(ω2 = ωLi2 ) и электронную ( (ω − kzu)2 = ωLe2 ). Инкремент (38.11) имеет структуру инкремента
(39.10), т.е. является инкрементом неустойчивости при одночастичном эффекте Черенкова. Однако, правое неравенство (38.10) свидетельствует, что это - коллективный эффект. Противоречия, конечно, никакого нет. Дело здесь в левом неравенстве (38.10), которое по смыслу противоположно неравенству (39.7). То есть по ионам (а в более общем смысле по волнам среды) резонансная неустойчивость Бунемана является одночастичным эффектом, но не эффектом Черенкова. По электронам же эта неустойчивость действительно является коллективным вынужденным эффектом Черенкова, в полном соответствии с классификацией, изложенной выше.
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Глава VIII. Неустойчивости электронных пучков
вконечном внешнем магнитном поле
§40. Общее уравнение линейной теории электростатических колебаний цилиндрического столба радиально неоднородной заряженной плазмы
ВГлаве V были рассмотрены стационарные равновесные состояния многокомпонентной аксиально симметричной заряженной плазмы, ориентированной вдоль внешнего одно-
родного конечного магнитного поля Br = {0,0, B0 } и состоящей из пучка электров и заряжен-
ных частиц других сортов, частично или полностью нейтрализующих статический заряд электронного пучка. Предполагалось, что плазма бесконечна и однородна вдоль оси z и все характеризующие ее величины зависят только от координаты r цилиндрической системы координат. Данная глава посвящена рассмотрению малых возмущений найденных ранее состояний равновесия, в том числе исследованию этих состояний на устойчивость.
Для описания динамики заряженных частиц используем систему уравнений многожидкостной гидродинамики, записанных для каждого сорта заряженных частиц плазмы в цилиндрической системе координат
∂∂Ntα + 1r ∂∂r (rNαVαr )+ 1r ∂∂ϕ (NαVαϕ )+ ∂∂z (NαVαz )= 0 ,
∂V |
|
∂V |
|
Vαϕ |
∂V |
|
+V |
∂V |
|
− |
Vαϕ2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
αr +V |
αr + |
|
r |
αr |
|
|
|
|
|
αr |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
αr |
∂r |
|
|
∂ϕ |
|
|
αz |
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eα |
|
Vα2 |
|
|
|
|
|
1 |
(Vαϕ B |
|
|
Bϕ )− |
|
1 |
|
|
|
|
|
r r |
|
|
|
= |
|
|
1 − |
|
|
E |
|
|
+ |
|
|
|
−Vα |
|
|
|
|
Vα |
(Vα E) , |
|
|
|
|
mα |
|
c2 |
|
|
c |
|
c2 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
z |
z |
|
|
|
r |
|
|
|
∂Vαϕ +V |
∂Vαϕ + Vαϕ ∂Vαϕ |
+V |
|
∂Vαϕ |
+ VαrVαϕ = |
|
|
|
|
|
|
|
|
|
|
|
∂t |
αr |
∂r |
|
|
r |
∂ϕ |
|
|
αz |
|
|
|
∂z |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eα |
|
|
Vα2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
r r |
|
|
|
= |
|
1 − |
|
|
E |
|
|
+ |
|
|
(V B |
−V B )− |
|
|
|
|
|
|
V |
|
(V E) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mα |
|
|
c2 |
|
ϕ |
|
|
c |
α |
z r |
α |
r z |
|
c2 |
|
|
αϕ |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V |
|
∂V |
|
Vαϕ |
∂V |
|
+V |
∂V |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αz +V |
αz + |
|
r |
αz |
|
|
|
|
|
αz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
αr |
∂r |
|
|
∂ϕ |
|
|
αz |
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eα |
|
|
Vα2 |
|
|
|
|
|
|
1 |
(Vα |
|
|
|
−Vαϕ B )− |
1 |
|
|
|
|
r r |
|
|
|
= |
|
1 − |
|
E |
|
|
+ |
|
|
|
Bϕ |
|
|
|
|
|
Vα |
(Vα E) . |
|
|
|
mα |
c2 |
|
|
c |
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
r |
|
|
|
r |
|
|
|
|
z |
|
|
Здесь (Vα E) =Vαr Er +Vαϕ Eϕ +Vαz Ez , Vα2 =Vα2r +Vαϕ2 +Vα2z . Релятивистские уравнения (40.2) по-
лучены очевидным объединением уравнений (18.8) и (18.12). Заметим, что релятивистским является только электронный пучок (α = b ). Частицы других сортов (α = e и α = i - электроны и ионы нейтрализующего фона) релятивистскими по существу не являются.
В соответствии с результатами Главы V, представим входящие в уравнения (40.1) и (40.2) величины в виде (см. также (19.5) и (19.6))

Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
r |
(s) |
|
|
~ |
|
|
r |
|
|
|
|
|
|
|
Nα (t, r ) = Nα |
|
(r) + Nα |
(t, r ) , |
|
|
(s) |
|
~ |
|
|
r |
r |
~ |
|
|
r |
(s) |
|
~ |
|
r |
|
|
r |
Vα (t, r ) = {Vαr |
(t, r ), Vαϕ |
(r) +Vαϕ (t, r ), Vαz (r) +Vαz (t, r )}, |
r |
r |
(s) |
|
|
~ |
|
r |
~ |
r |
~ |
|
r |
|
|
(40.3) |
E(t, r ) |
= {Er |
(r) + Er (t, r ), Eϕ |
(t, r ), Ez (t, r )}, |
~ |
|
r |
r |
~ |
|
r |
(s) |
|
|
~ |
r |
|
|
(s) |
|
r |
|
|
|
|
|
|
|
|
+ Bz |
|
|
B(t, r ) |
= {Br (t, r ), Bϕ |
|
(r) + Bϕ (t, r ), B0 |
(r) + Bz (t, r )}. |
Здесь величины с индексом “ (s) ” характеризуют состояние равновесия, величины со знаком
“~” являются малыми возмущениями, B0 - продольная составляющая внешнего магнитного поля, а r ={r,ϕ, z}. Равновесные величины определяются формулами (21.1)-(21.3), (21.6) и
связаны между собой уравнением баланса радиальных сил (21.8). Как показано в § 21 при определении равновесных конфигураций цилиндрически симметричной заряженной плазмы в магнитном поле имеется определенный произвол (в § 21 при обозначении равновесных величин индекс “ (s) ” был для сокращения записей опущен).
Дальнейшая задача состоит в получении и исследовании замкнутых уравнений для малых возмущенных величин. Однако, учет всех введенных в формулах (40.3) возмущений достаточно сложен. Поэтому ограничимся только потенциальным (электростатическим) приближением. В этом приближении (см. § 19) можно пренебречь возмущением магнитного поля, B~r = B~ϕ = B~z = 0 , а возмущение электрического поля выразить через возмущение ска-
лярного потенциала ϕ~(t, rr)
~ |
|
|
~ |
|
|
~ |
|
|
1 |
~ |
|
~ |
~ |
|
|
|
|
|
∂ϕ |
|
|
|
|
∂ϕ |
|
∂ϕ |
|
|
|
|
Er = − |
|
, |
Eϕ = − |
|
|
|
|
, |
Ez = − |
|
, |
|
(40.4) |
∂r |
|
r |
∂ϕ |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
который, в свою очередь, определяется из уравнения Пуассона (см. уравнение (19.20)) |
|
|
1 ∂ |
|
~ |
|
|
|
|
2 ~ |
|
|
2 |
~ |
|
|
~ |
r |
|
|
|
∂ϕ |
|
1 ∂ ϕ |
|
|
∂ ϕ |
|
|
|
|
|
|
|
|
r |
|
+ |
|
|
|
|
2 |
+ |
|
2 |
|
= −4π∑eα Nα (t, r ) . |
(40.5) |
|
r ∂r |
∂r |
r |
2 |
∂ϕ |
∂z |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
При получении последнего уравнения было учтено первое соотношение (21.6), записанное для равновесных величин Er(s) (r) и Nα(s) (r) .
Предположим также, что равновесное поперечное (вращательное) движение частиц любого сорта является нерелятивистским, а также нерелятивистскими оказываются все возмущения скоростей, т.е. выполнены следующие неравенства:
(s) |
~ |
c <<1. |
(40.6) |
Vαϕ |
c <<1, Vαr,ϕ,z |
Первое из указанных неравенств позволяет пренебречь диамагнетизмом плазмы, т.е. поло-
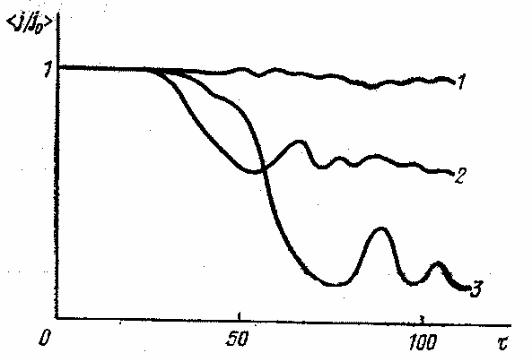
жить собственное продольное магнитное поле равным нулю: Bz(s) = 0 . Что касается собст-
венного азимутального магнитного поля Bϕ(s) , то из-за возможного релятивизма продольного движения пучка, Vbz(s) 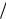 c →1, им пренебрегать нельзя. Поле Bϕ(s) (r) определяется третьим со-
c →1, им пренебрегать нельзя. Поле Bϕ(s) (r) определяется третьим со-
Александров А.Ф., Кузелев М.В. Физика электронных пучков
отношением (21.6).
Подставляя выражения (40.3) в уравнения (40.1), (40.2) и учитывая сделанные выше предположения, получим следующую гидродинамическую систему линейного приближения:
|
∂ |
|
(s) |
|
∂ |
|
|
Vαϕ(s) |
|
|
+V |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
∂t |
αz |
|
∂z |
|
|
r |
|
|
|
|
|
|
|
|
|
∂ |
|
(s) |
|
∂ |
|
|
Vαϕ(s) |
|
|
+V |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
∂t |
αz |
|
∂z |
|
|
r |
|
|
|
|
|
|
|
|
|
∂ |
|
(s) |
|
∂ |
|
|
Vαϕ(s) |
|
|
+V |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
∂t |
αz |
|
∂z |
|
|
r |
|
|
|
|
|
|
|
|
|
∂ |
|
(s) |
|
∂ |
|
|
Vαϕ(s) |
|
|
+V |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
∂t |
αz |
|
∂z |
|
|
r |
|
|
|
|
|
|
|
|
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
(r)] |
2 |
|
|
|
− |
[Vαz |
|
|
γα = 1 |
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ ~ ∂ϕ Nα
∂ ~ ∂ϕ Vαr
∂ ~ ∂ϕ Vαϕ
∂ ~ ∂ϕ Vαz
−1 2
-
|
1 |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
(s) ~ |
|
|
|
|
(s) |
1 ∂Vαϕ |
|
|
|
(s) |
∂V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
αz |
|
|
|
+ |
|
|
|
|
|
(rNα Vαr ) |
+ Nα |
|
|
|
+ Nα |
|
|
∂z |
= 0 , |
|
r |
∂r |
r |
∂ϕ |
|
|
|
|
|
|
|
|
|
(s) |
|
|
|
|
e B |
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
Vαϕ |
|
|
|
|
|
|
−1 |
~ |
|
|
|
|
−1 |
∂ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α 0 |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
− |
|
2 |
|
|
|
+ |
|
|
|
|
|
|
γ |
α |
Vαϕ = − |
|
|
γα |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
mα с |
|
|
|
|
|
|
|
|
|
|
mα |
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂Vαϕ |
|
|
Vαϕ |
|
e B |
|
|
|
|
|
|
|
|
|
e |
|
|
|
~ |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
−1 |
1 ∂ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
0 |
|
~ |
|
|
|
|
|
α |
|
|
|
|
|
+ |
|
|
+ |
|
|
|
+ |
|
|
|
|
γα |
Vαr |
= − |
|
|
γ |
α |
|
∂ϕ |
, |
|
∂r |
|
|
r |
|
|
m с |
m |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(s) |
|
|
|
|
eα |
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ ∂Vαz |
|
|
|
|
|
|
−3 ∂ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
+Vαr |
|
|
|
|
= − |
|
γα ∂z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
mα |
|
|
|
|
|
|
|
|
|
|
|
|
невозмущенный продольный релятивистский фактор частиц сорта α . При получении уравнений (40.7) было учтено уравнение баланса радиальных сил (см. (21.8))
|
(Vαϕ(s) )2 |
|
eα |
|
−1 |
|
(s) |
|
1 |
|
(s) |
|
|
1 |
|
(s) |
|
(s) |
|
− |
|
= |
|
γ |
|
E |
|
+ |
|
V |
|
B |
− |
|
V |
|
B |
|
, |
(40.9) |
r |
mα |
|
|
c |
|
|
|
|
|
|
|
α |
|
r |
|
αϕ |
0 |
|
c αz |
ϕ |
|
|
а релятивистский фактор (40.8) вычислялся в нулевом приближении по параметрам (40.6). Кроме того, были использованы соотношения (40.4).
Представим возмущения потенциала, плотностей и компонент скоростей в виде
~ |
|
|
|
|
ϕ(t, r,ϕ, z) =ψ (r) exp(−iωt + ikz z + ilϕ) , |
|
~ |
~ |
(r) exp(−iωt + ik |
z + ilϕ) , |
|
N |
(t, r,ϕ, z) = n |
|
~α |
α |
z |
|
|
Vαr (t, r,ϕ, z) = vαr (r) exp(−iωt + ikz z + ilϕ) , |
(40.10) |
~ |
|
|
|
|
Vαϕ (t, r,ϕ, z) = vαϕ (r) exp(−iωt + ikz z + ilϕ) , |
|
~ |
(t, r,ϕ, z) = vαz (r) exp(−iωt + ikz z + ilϕ) , |
|
Vαz |
|
где ω - частота, kz - продольное волновое число, l = 0,±1,±2,...- азимутальное волновое число.
Подстановка решений (40.10) во второе, третье и четвертое уравнения системы (40.7) приводит к следующей системе алгебраических уравнений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i∆ |
|
(r)v |
+ Ω |
|
(r)v |
|
|
= |
eα |
γ −1 |
dψ |
, |
|
|
|
|
|
mα |
|
|
|
|
|
|
α |
αr |
|
|
2α |
|
αϕ |
|
|
|
|
|
α |
dr |
|
|
i∆ |
|
(r)v |
− Ω |
(r)v |
|
|
= i |
eα |
|
γ −1 |
|
l |
ψ , |
(40.11) |
|
|
|
mα |
|
|
|
α |
αϕ |
|
|
1α |
|
αr |
|
|
|
|
|
α |
|
r |
|
|
i∆ |
|
(r)v |
− |
dV (s) |
(r) |
v |
|
= ik |
|
|
e |
|
γ −3ψ. |
|
|
|
αz |
|
|
|
|
α |
|
|
|
|
dr |
|
|
z mα |
|
|
|
α |
αz |
|
|
|
|
αr |
|
|
|
|
|
α |
|
|


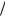 ΩLe , что взято при построении дисперсионных кри-
ΩLe , что взято при построении дисперсионных кри-