
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
Александров А.Ф., Кузелев М.В. Физика электронных пучков
проницаемость ε0 меньше нуля. При апериодической пучковой неустойчивости в плазме от-
рицательность диэлектрической проницаемости плазмы обеспечивается именно движением электронов пучка. Пучок, имеющий затравочную модуляцию на длине волны 2π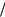 | kz | , дей-
| kz | , дей-
ствует на плазму с вынуждающей силой на частоте | ω | = | kz | u < ωLe . Происходит вынуж-
денная поляризация плазмы в поле пространственного заряда пучка. Отклик плазмы на такое воздействие характеризуется ее отрицательной в данной области частот диэлектрической проницаемостью (32.14). Но это не статическая диэлектрическая проницаемость ε0 , а дина-
мическая εe .
При | kz | u = ωLe величина εe из (32.14) обращается в ноль, и выражения (32.10) и (32.16) становятся неприменимыми. Равенство kzu = ±ωLe означает совпадение частоты вы-
нуждающей силы со стороны пучка и частоты собственных ленгмюровских колебаний электронов плазмы, т.е. возникновение резонанса. Решения дисперсионного уравнения (32.4) при этом определяются формулами (32.11). Среди решений δω из (32.11) одно имеет положительную мнимую часть. Следовательно, в резонансе пучково-плазменная неустойчивость сохраняется. Более того, инкремент этой резонансной неустойчивости в силу (32.8) существенно больше инкремента нерезонансной апериодической неустойчивости (32.10). Равенство kzu = ±ωLe означает совпадение фазовой скорости собственной волны плазмы и скорости электрона пучка, что является известным условием возникновения излучения Вавилова – Черенкова (*). Таким образом, резонансная пучковая неустойчивость в плазме есть вынужденное черенковское излучение плазменной волны электронами пучка.
Заметим, что резонансная неустойчивость апериодической не является. Действитель-
но, как следует из (32.11), в системе покоя пучка частота волны ω − kzu имеет отличную от нуля действительную часть. Между апериодической и резонансной неустойчивостями имеется важное различие. Апериодическая неустойчивость не связана с излучением, а приводит лишь к модуляции пучка. Наоборот, резонансная неустойчивость приводит к интенсивному возбуждению электронным пучком плазменных колебаний.
Для детального анализа дисперсионного уравнения (32.4), а точнее, его упрощенного аналога (32.9), введем безразмерные величины: безразмерный инкремент неустойчивости
δ = |
δω |
(ω = kzu(1+δ)), |
(32.17) |
|
kzu |
|
|
безразмерную расстройку черенковского резонанса
(*) Это излучение было открыто как излучение поперечных электромагнитных (световых) волн в среде прямолинейно движущимся электроном. Оно, однако, возможно в любой замедляющей волны среде при самой разнообразной поляризации и природе волн. Поляризация определяет диаграмму направленности излучения.
151
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|
∆ = |
|
k 2u2 |
−ω2 |
(32.18) |
||
|
|
z |
Le |
|
||
|
|
2ωLe2 |
||||
|
|
|
|
|||
и малый параметр, характеризующий выполнимость неравенства (32.5) |
|
|||||
|
1 |
ωLb2 γ −3 |
|
|||
ν = |
|
ωLe2 . |
(32.19) |
|||
2 |
||||||
В новых переменных уравнение (32.9) записывается в виде |
|
|||||
δ 2 (δ + ∆)=ν . |
(32.20) |
|||||
Комплексное решение уравнения (32.20) с положительной мнимой частью, т.е. соответствующее неустойчивой волне, имеется при
∆ < |
|
|
3 |
ν1 3 . |
|
|
|
|
|
|
|
|
|
(32.21) |
|||||||
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Мнимая и действительная части δ |
выражаются по формулам Кардана |
||||||||||||||||||||
Imδ |
|
= i |
|
3 |
(G(+) |
−G(−)), |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Reδ = − |
1 |
|
(G(+) + G(−)), |
|
|
|
|
(32.22) |
|||||||||||||
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(±) |
|
|
|
3 |
|
∆3 |
|
ν |
|
|
|
|
∆3 |
|
ν |
|
|||
G |
|
= |
− |
|
|
|
+ |
|
± −ν |
|
|
− |
|
|
|||||||
|
|
|
|
27 |
2 |
|
27 |
4 |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
В размерной форме неравенство (32.21) записывается как |
|||||||||||||||||||||
k |
2 |
< |
ω2p |
|
|
|
|
6 |
ν |
1 3 |
|
|
|
|
|
(32.23) |
|||||
z |
|
|
u2 |
1+ |
|
|
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 4 |
|
|
|
|
|
|
|
|
||||
что определяет область неустойчивости пучково-плазменной системы между метками «1» и «2» на оси волновых чисел kz на Рис. 32.1.
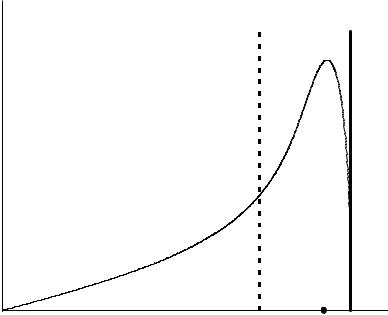
На Рис. 32.2 представлена зависимость безразмерной величины y = (kzu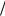 ωLe )| Imδ | от безразмерного волнового числа x = kzu
ωLe )| Imδ | от безразмерного волнового числа x = kzu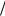 ωLe , полученная по формулам (32.22). Вертикальную пунктирную линию условно можно считать границей между областью резонансной не апериодической пучковой неустойчивости и областью нерезонансной апериодической неустой-
ωLe , полученная по формулам (32.22). Вертикальную пунктирную линию условно можно считать границей между областью резонансной не апериодической пучковой неустойчивости и областью нерезонансной апериодической неустой-
чивости. Максимум безразмерного инкремента ymax = ( 3 2)ν1 3 достигается при |
x =1, т.е. |
||||
при точном черенковском резонансе, когда расстройка (32.18) равна нулю. |
|
||||
Заметим, что можно ввести “абсолютные” безразмерные инкремент δ~ = δν −1 3 и рас- |
|||||
~ |
|
−1 3 |
. При этом уравнение (32.20) записывается в следующей универсальной |
||
стройку ∆ = ∆ν |
|
||||
форме: |
|
|
|
|
|
~2 |
~ |
~ |
|
|
(32.24) |
δ |
(δ |
+ ∆) =1, |
|||
не содержащей ни одного свободного параметра. В частности, | δ~ |max =1. 152
Александров А.Ф., Кузелев М.В. Физика электронных пучков
y |
|
1 |
x |
Рис. 32.2 |
|
Зависимость от безразмерного волнового числа x безразмерного инкремента y пучковой неустойчивости в плазме.
153

Александров А.Ф., Кузелев М.В. Физика электронных пучков
§ 33. Формальное решение кинетического уравнения Власова
Из дальнейшего будет ясно, что адекватное описание нелинейной динамики пучковой неустойчивости в плазме возможно только при использовании кинетического уравнения Власова. Решение кинетического уравнения связано с серьезными математическими трудностями. Многие пучковые и плазменные неустойчивости исследуются в постановке так называемой начальной задачи, когда описывающие неустойчивую физическую систему уравнения дополняются периодическими по пространству граничными условиями. В подобной ситуации решение кинетического уравнения Власова целесообразно записывать в виде интеграла по начальным данным характеристической системы этого уравнения. Построению такого формального решения посвящен данный параграф.
Исходим из следующего простейшего кинетического уравнения (17.10) для функции
распределения fα (t, z, p) |
|
|
частиц сорта α , совершающих одномерное движение вдоль оси |
||||||||||||||||||||||||||||||||||||||||||||||||
OZ в электрическом поле Ez (t, z) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
∂fα |
|
+ v |
∂fα |
|
+ e E |
|
|
∂fα |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.1) |
|||||||||||||||||||||
|
∂t |
∂z |
|
z |
∂p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Здесь p - продольная составляющая импульса, а |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
v = c |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.2) |
|||||||||
mα2 c2 + p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
скорость частиц. Обозначим через z(t, z |
0 |
, p |
0 |
) и |
|
p(t, z |
0 |
, p |
0 |
) |
решения характеристической сис- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
||||
темы уравнения (33.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
dz |
|
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
ˆ |
= v, |
|
|
|
|
|
|
ˆ |
= e E |
z |
(t, z) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.3) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
dt |
ˆ |
|
|
|
|
dt |
|
|
|
|
|
α |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
дополненной начальными условиями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
z |
|
|
|
|
|
= z |
|
, |
|
|
|
p |
|
|
|
|
= p |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
ˆ |
|
t |
=0 |
|
|
0 |
|
|
|
|
ˆ |
|
|
t=0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Покажем, что если в начальный момент времени |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
fα (t, z, p) |
|
t=0 = f0α ( p) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.5) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
то во все последующие моменты функция распределения определяется выражением |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
f |
α |
(t, z, p) = |
∫∫ |
dz |
0 |
dp |
0 |
f |
0α |
( p |
0 |
|
ˆ |
|
|
|
0 |
, p |
0 |
|
|
ˆ |
|
|
0 |
, p |
0 |
)]. |
(33.6) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
)δ[z − z(t, z |
|
|
)]δ[p − p(t, z |
|
|
||||||||||||||||||||||||||||||||||
Подставляя в формулу (33.6) t = 0 и учитывая начальные условия (33.4), находим, что |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
fα (0, z, p) = ∫∫dz0dp0 f0α ( p0 )δ(z − z0 )δ( p − p0 ) . |
|
|
|
|
|
|
|
|
|
(33.7) |
||||||||||||||||||||||||||||||||||||||||
Учитывая далее основное свойство δ -функции |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
∫ϕ(x)δ(x − a)dx = ϕ(a) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.8) |
||||||||||||||||||||||||||||||
154
Александров А.Ф., Кузелев М.В. Физика электронных пучков
получаем из (33.7) соотношение (33.5). Таким образом функция распределения (33.6) удовлетворяет начальному условию (33.5). Остается только проверить, что функция (33.6) удовлетворяет кинетическому уравнению (33.1). Сделаем это прямой подстановкой. С учетом характеристической системы (33.3) имеем:
|
∂fα |
= − |
∫∫ |
|
0 |
dp |
0 |
f |
0α |
( p |
0 |
|
|
|
ˆ |
|
′ |
|
p |
|
α |
|
z |
|
|
ˆ |
|
z |
|
|
′ |
|
}, |
|
|
|
||||||||||
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
z |
δ |
|
|
|
|
|
δ |
p |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
dz |
|
|
|
|
|
){vδ |
|
|
+ e E |
|
(t, z)δ |
|
|
|
|
(33.9) |
||||||||||||||||||||||||
|
|
|
∂fα |
|
|
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂fα |
|
|
|
|
∫∫ |
|||||||
v |
= v |
dz0dp0 f0α ( p0 )δz′δp , eα Ez (t, z) |
|
= eα Ez (t, z) |
dz0dp0 f0α ( p0 )δzδ′p . |
|||||||||||||||||||||||||||||||||||||||||
∂z |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|||||||
Здесь δ |
z |
≡ δ[z − z(t, z |
0 |
, p |
0 |
)], δ |
p |
|
≡ δ[p − p(t, z |
0 |
, p |
0 |
)], а “штрих” означает дифференцирование. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подстановка (33.9) в левую часть уравнения (33.1) приводит к следующему выражению: |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∫∫ |
|
0 |
|
|
|
|
0 |
0α |
|
|
|
|
0 |
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
z |
|
|
|
|
|
|
|
|||
|
F(t, z, p) ≡ dz dp f ( p )(v − v)δ( p − p)δ |
′ |
|
+ |
|
|
(33.10) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
α |
∫∫ |
|
|
0 |
dp |
0 |
f |
0α |
( p |
0 |
)[E |
z |
(t, z) − E |
z |
|
|
|
ˆ |
ˆ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ e |
|
|
|
dz |
|
|
|
|
|
|
|
(t, z)]δ(z − z)δ′. |
|||||||||||||||||||||||||
Для доказательства того, что функция (33.6) является решением уравнения (33.1), требуется показать, что выражение (33.10) тождественно равно нулю.
Вычислим якобиан преобразования от переменных z, |
p к переменным |
z |
0 |
, p |
0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
||
|
|
|
∂(z, |
p) |
|
|
∂z ∂z |
|
|
|
∂z ∂p |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ˆ |
|
0 |
|
|
|
|
ˆ |
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
D(t) = |
|
|
ˆ |
|
ˆ |
|
|
) = |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
(33.11) |
||||
|
∂(z |
0 |
, p |
0 |
|
∂p |
∂z |
0 |
|
∂p |
∂p |
0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
||||||
При t = 0 , согласно (33.4), |
|
z = z |
0 |
и |
p = p |
0 |
, а следовательно, |
D(0) =1. В момент времени ∆t |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
||
( ∆t → 0 ) из характеристических уравнений имеем |
|
|
|
|
|
|||||||||||||||||||||||||||
|
z = z |
0 |
+ v |
∆t, |
|
|
p = p |
0 |
+ e E |
z |
(0, z |
0 |
)∆t , |
|
|
|
|
(33.12) |
||||||||||||||
|
ˆ |
0 |
|
|
|
|
|
|
ˆ |
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где v0 и p0 |
связаны так же, как v и p в (33.2). Подставляя (33.12) в (33.11) находим, что |
|||||||||||||||||||||||||||||||
|
D(∆t) =1− eα |
|
dv0 |
|
∂Ez (0, z0 ) |
(∆t)2 . |
|
|
|
|
|
|
|
(33.13) |
||||||||||||||||||
|
dp0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dD(0) |
= lim |
D(∆t) − D(0) |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
(33.14) |
||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
∆t→0 |
|
|
|
|
∆t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как выбор начала отсчета времени произволен, то соотношение (33.14) верно при любом t , а не только при t = 0 . Учитывая, что D(0) =1, окончательно получаем
|
|
|
|
|
D(t) ≡1 |
(33.15) |
||
или dz |
dp |
0 |
= dzdp , что отражает теорему Лиувилля о сохранении фазового объема. |
|||||
|
|
|
|
0 |
|
ˆ |
ˆ |
|
|
|
|
|
Учитывая теорему Лиувилля, сделаем в (33.10) замену переменных интегрирования |
||||
z |
0 |
, p |
0 |
→ z, p , что дает |
||||
|
|
|
ˆ |
ˆ |
|
|||
155

|
∫∫ |
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
|
|
|
||||||||||||||||||
F(t, z, p) = |
|
ˆ ˆ |
0α |
ˆ0 |
|
|
|
|
ˆ ˆ |
|
ˆ |
z |
|
|
|
|
|
|
|
|
|
|||
|
dzdpf |
|
[p |
|
(t, z, p)](v( p) − v( p))δ( p − p)δ′ + |
|
|
|
|
|
|
|
(33.16) |
|||||||||||
|
+ e |
|
dzdpf |
|
|
[p |
(t, z, p)][E |
|
(t, z) − E |
|
(t, z)]δ(z |
− z)δ′. |
|
|
|
|||||||||
|
|
0α |
z |
z |
|
|
|
|
||||||||||||||||
|
|
α ∫∫ |
|
ˆ |
ˆ |
ˆ0 |
|
|
ˆ |
|
|
ˆ |
|
p |
|
|
|
|
||||||
Здесь функция p |
(t, z, p) |
определяется из уравнений |
|
z = z(t, z |
0 |
, p |
0 |
) |
и p = p(t, z |
0 |
, p |
0 |
) , а v( p) |
|||||||||||
ˆ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
ˆ |
|
|
||||
и vˆ( pˆ ) - функции (33.2); ни одна из перечисленных функций особенностей не имеет. Исполь-
зуя теперь тривиальное следствие основного свойства δ -функции (33.8)
∫[ϕ(x) −ϕ(a)]δ(x − a)dx = 0 , |
(33.17) |
находим, что выражение (33.16) тождественно равно нулю. Таким образом, доказано, что функция (33.6), называемая интегралом по начальным данным, является решением кинетического уравнения Власова (33.1) с начальным условием (33.5). Безусловно это - формальное решение, представляющее только иную форму записи исходного уравнения. Однако, в последствии мы убедимся, что с помощью формального решения (33.6) в ряде случаев удается решать сложные задачи.
Используя решение (33.6) и общие формулы (17.11), запишем следующие выражения для возмущений плотности заряда и тока частиц сорта α :
ρ |
α |
α |
∫∫ |
|
|
|
0 |
dp |
0 |
f |
0α |
( p |
0 |
|
|
|
|
ˆ |
|
|
0 |
, |
p |
0 |
)], |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(t, z) = e |
|
|
dz |
|
|
|
|
|
|
|
)δ[z − z(t, z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(t, z |
|
, p |
|
) |
|
|
|
|
|
|
|
|
|
(33.18) |
|||||||
j |
|
(t, z) = e c |
|
|
dz |
|
dp |
|
f |
|
( p |
|
|
) |
|
|
|
|
|
|
|
δ |
[z − z(t, z |
|
, p |
|
)]. |
|||||||||||||||||||
α |
α |
|
∫∫ |
|
|
|
0 |
|
|
|
0 |
|
|
0α |
|
|
0 |
|
|
m2 c2 |
+ p2 (t, z |
0 |
, p |
0 |
) |
|
ˆ |
0 |
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае начального распределения вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
f0α ( p) = n0αδ( p − p0α ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.19) |
|||||||||||||||||
описывающего холодную систему частиц ( n0α - плотность частиц, |
p0α - общий для всех час- |
|||||||||||||||||||||||||||||||||||||||||||||
тиц импульс), формулы (33.18) упрощаются: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
ρ |
α |
(t, z) = e n |
|
∫ |
dz |
δ[z − z(t, z |
0 |
)], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
α |
|
0α |
|
|
|
0 |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(33.20) |
||||||
j |
|
(t, z) = e n |
c |
|
|
dz |
|
|
|
|
|
|
p(t, z |
) |
|
|
δ[z − z(t, z |
|
)]. |
|
|
|
|
|
||||||||||||||||||||||
α |
α |
|
0α |
|
|
∫ |
|
|
|
0 |
|
|
|
m2 c2 |
|
+ p2 |
(t, z |
0 |
) |
|
|
|
|
|
|
|
ˆ |
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Формулы (33.6), (33.18) и (33.20) очевидным образом обобщаются на многомерный случай.
§34. Нелинейные уравнения пучковой неустойчивости в плазме
В§ 32 в линейном приближении была рассмотрена безграничная однородная пучко- во-плазменная система и ее неустойчивость относительно одномерных потенциальных возмущений, зависящих только от координаты в направлении движения пучка (ось OZ ). Проведем теперь соответствующее нелинейное рассмотрение. Исходим из следующих нелинейных уравнений:
156

Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
∂Ez |
= 4πe |
∑ |
n |
|
|
∫ |
dz |
δ |
(z − z (t, z |
0 |
)), |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∂z |
|
|
|
0 |
α |
|
0 |
|
|
ˆα |
|
|
|
||||||||||
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
(34.1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dz |
|
|
|
|
dp |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ˆα |
= v , |
|
|
|
ˆα |
|
|
= eE |
z |
(t, z ). |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dt |
ˆα |
|
|
|
dt |
|
|
|
|
|
|
|
ˆα |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнения движения в системе (34.1) дополняются начальными условиями |
||||||||||||||||||||||||
|
z |
|
|
= z |
|
, |
|
p |
|
|
|
|
= p |
|
. |
|
|
|
(34.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ˆα |
|
t=0 |
|
0 |
|
|
|
ˆα |
|
t=0 |
|
|
|
0α |
|
|
|
|
(α = e − электроны плазмы, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Здесь |
n0α - невозмущенные плотности частиц сорта |
α |
||||||||||||||||||||||
α = b - электроны пучка), |
а |
p0α - их невозмущенные импульсы. Для холодной покоящейся |
||||||||||||||||||||||
плазмы |
p0e |
= 0 , |
|
а для релятивистских электронов пучка |
p0b |
= m(1−u2 c2 )−1 2 , где u − невоз- |
||||||||||||||||||
мущённая скорость электронов пучка. Связь между скоростями и импульсами электронов дается формулами
v |
= |
cpb |
, v |
e |
= pe , |
(34.3) |
|
b |
m2c2 + pb2 |
|
m |
|
|
|
|
|
|
|
Поясним, что первое уравнение в (34.1) является уравнением Пуассона для напряженности электрического поля, а плотности заряда электронов плазмы и пучка записаны через интегралы по начальным данным в предположении, что в начальный момент разброс по скоростям у электронов отсутствует (см. первую формулу (33.20)).
Будем рассматривать пучковую неустойчивость в постановке начальной задачи, для чего предположим, что начальное возмущение пучково-плазменной системы имеет пространственный период L . Тогда все возмущенные величины, в том числе, и электрическое поле Ez можно представить в виде следующего ряда:
E |
(t, z) = |
1 |
∞ (E |
(t)exp(ink |
z) +C.C.), |
(34.4) |
||
2 |
||||||||
z |
|
∑n=1 |
n |
z |
|
|
||
где kz = 2π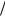 L − основное продольное волновое число. Подставляя (34.4) в первое уравнение
L − основное продольное волновое число. Подставляя (34.4) в первое уравнение
(34.1), интегрируя его по z |
от нуля до L и учитывая ортогональность функций exp(inkz z) , |
||||||||||||||||||||||||||||||
получим следующие выражения для коэффициентов разложения En (t) в (34.4): |
|||||||||||||||||||||||||||||||
E |
n |
(t) = − |
i |
4πe(n |
ρ |
bn |
+ n |
ρ |
en |
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
(34.5) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
nkz |
0b |
|
|
0e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где ραn − амплитуды гармоник возмущений плотностей пучка и плазмы, |
вычисляемые по |
||||||||||||||||||||||||||||||
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ρ |
αn |
= |
1 |
2πexp(−iny (t, y |
0 |
))dy |
0 |
, |
y |
(t, y |
0 |
) = k |
z |
(t, z |
0 |
), |
y |
0 |
= k |
z |
z |
. |
(34.6) |
||||||||
π |
|||||||||||||||||||||||||||||||
|
|
∫ |
α |
|
|
|
|
|
|
α |
|
|
z ˆα |
|
|
|
|
0 |
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, что ραn |
определяют безразмерные амплитуды пространственных Фурье - гармо- |
||||||||||||||||||||||||||||||
157
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ник возмущений плотности соответствующей системы частиц, а размерные амплитуды даются величинами n0α ραn . При получении (34.6) учтено свойство (33.8).
Подставляя далее (34.5) и (34.4) в уравнения движения электронов из системы (34.1), приходим к следующим нелинейным уравнениям:
d2 ye |
= − |
1 |
i∑∞ |
1 |
[(ωLe2 |
ρen +ωLb2 ρbn )exp(inye ) −C.C.], |
|
||||||
2 |
|
n |
|
||||||||||
dt |
|
2 n=1 |
|
|
|
|
|
|
|
||||
|
|
|
|
vb |
|
|
|
|
|
∞ |
[(ωLb2 ρbn +ωLe2 ρen )exp(inyb ) −C.C.], |
|
|
kz |
d |
1 |
|
|
|
= − |
1 i∑1 |
(34.7) |
|||||
|
dt |
−v2 |
c2 |
|
|
2 n=1 n |
|
|
|||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
dydt2b = kzvb.
Уравнения (34.7) являются точными, поскольку учитывают все нелинейные эффекты, могущие быть существенными в рамках принятой модели пучково-плазменной системы. К таковым эффектам относятся: зависимость массы релятивистских электронов пучка от скорости; отклонение траекторий электронов пучка и плазмы от их невозмущенных траекторий на расстояние порядка длины волны – нелинейные члены~ exp(inyα ) ; генерация гармоник плотно-
сти заряда частиц – суммы по n в уравнениях движения.
При анализе уравнений (34.7) ограничимся случаем электронных пучков малой плотности. Оказывается, что при этом плазма в течение достаточно длительного периода развития и стабилизации неустойчивости остается линейной. Получим условие, при котором нелинейность движения электронов пучка является определяющей, а электроны плазмы можно описывать в линейном приближении. При качественном рассмотрении оценочного характера уравнения движения электронов пучка и плазмы можно записать в виде
|
|
2 |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
zb |
= |
e |
γ −3 E |
0 |
cos(ωt − k |
z |
z) |
|
|
, |
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt |
2 |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
z=ut+z0 |
|
|
(34.8) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
|
ze |
|
= |
|
e |
|
E |
0 |
cos(ωt − k |
z |
z) |
|
|
|
, |
|
|
|
|||||||
|
dt |
|
|
m |
z |
=z0 |
|
|
|
|||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где E0 - амплитуда, а |
|
~ |
− ut |
− z0 и |
~ |
- возмущения траекторий пучка и плазмы |
||||||||||||||||||||||
|
zb = zb |
ze = ze − z0 |
||||||||||||||||||||||||||
соответственно. Учитывая (32.7) и (32.8), из (34.8) имеем следующую оценку: |
||||||||||||||||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
kz zb |
≈ |
|
|
|
|
kz u |
|
|
|
, |
|
|
|
|
|
|
|
|
|
(34.9) |
|||||||
|
|
|
~ |
|
|
γ |
3 |
| δω |
| |
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
kz ze |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
нелинейность движения |
где δω определен в (32.10) или (32.11). Очевидно, что при | kz zb |≈1 |
||||||||||||||||||||||||||||
~ |
, то электроны плазмы можно рас- |
электронов пучка существенна, а если при этом | kz ze | <<1 |
сматривать в линейном приближении. Отсюда и находим критерий справедливости линейного приближения для описания плазмы
158

Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
γ 3 | δω |2 << kz2u2 , |
(34.10) |
Позднее, при рассмотрении конкретных режимов пучковой неустойчивости в плазме, мы придадим неравенству (34.10) более явную форму. Теперь же, считая неравенство (34.10) выполненным и линеаризуя первое уравнение системы (34.7), получим следующие уравнения:
d2 ρ |
|
+ω2 |
ρ |
|
= −ω2 |
ρ |
, |
n =1,2,K, |
|
|
||||||
|
en |
|
|
|
||||||||||||
dt2 |
|
Le |
|
en |
|
|
|
Lb |
bn |
|
|
|
|
|
||
kz d |
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
ρen )exp(inyb ) −C.C.], |
|
|
|
vb |
|
|
|
|
= −1 i∑1 [(ωLb2 ρbn +ωLe2 |
(34.11) |
|||||||||
dt |
1−v2 |
c2 |
|
2 |
n=1 |
|
n |
|
|
|
||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
dyb |
= k v , |
|
y |
|
|
|
= y , |
v |
|
|
=u. |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
dt |
|
z b |
|
b |
|
t=0 |
|
0 |
b |
|
t=0 |
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Записывая систему (34.11), мы привели для полноты и начальные условия для уравнений движения электронов пучка, означающие, что при t = 0 пучок не возмущен.
Преобразуем уравнения (34.11), сделав следующие замены: |
|
|||||
yb = kzut + y( y0 |
,t), υ = |
vb −u |
, |
. |
(34.12) |
|
u |
||||||
|
|
|
||||
ρen = ρn (t) exp(−inkzut).
Первые две из них учитывают начальные условия для уравнений движения электронов пучка, а третья – вводит медленно меняющиеся амплитуды гармоник возмущения плотности плазмы ρn (t) . Медленность изменения этих амплитуд следует из (32.7) и неравенства (32.8).
Заметим, что поскольку плазма описывается в линейном приближении, генерация гармоник ее плотности может быть обусловлена только нелинейными процессами в пучке. Предположим еще, что изменение относительной скорости электронов пучка мало, т.е. выполнено неравенство
|
vb −u |
|
|
|
|υ |= |
<<1, |
(34.13) |
||
u |
||||
|
|
|
что фактически сводится к (32.8). Подставляя (34.12) в уравнения (34.11) и учитывая мед-
ленность изменения амплитуд ρn (t) |
и неравенство (34.13), получим следующую систему: |
||||||||||
2inkzu |
dρn |
|
+ [(nkzu)2 −ωLe2 ]ρn |
= ωb2 ρbn , |
n =1,2,K, |
|
|||||
dt |
|
||||||||||
|
dy |
|
|
|
|
|
|
|
|
|
|
|
= kzuυ, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
. |
(34.14) |
||||
|
dt |
|
|
|
|
||||||
kzu |
dυ |
= − |
|
1 |
iγ −3 (1 − 2β 2γ 2υ)3 2 ∑∞ 1 [(ωLb2 |
ρbn +ωLe2 ρn )exp(iny) − C.C.], |
|
||||
|
2 |
|
|||||||||
|
|
|
dt |
|
n=1 n |
|
|
||||
y t=0 = y0 , υ t=0 = 0.
Здесь величины
159

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ρbn = |
1 |
2∫πexp(−iny)dy0 |
(34.15) |
π |
|||
0 |
|
||
отличаются фазовым множителем exp(−inkzut) |
от тех, что определены в (34.6). Новые обо- |
||
значения для них не вводятся, поскольку к недоразумениям это привести не может. Дальнейший анализ уравнений (34.14) зависит от режима пучковой неустойчивости в плазме.
§ 35. Нелинейная теория резонансной пучково-плазменной неустойчивости
Предположим, что черенковский резонанс имеет место вблизи первой (основной)
пространственной гармоники начального возмущения, т.е ωLe2 ≈ kz2u2 . Тогда из первых урав-
нений системы (34.14) находим
2ikzu |
dρ1 |
+ [(kzu)2 −ωLe2 ]ρ1 = ωLb2 ρb1 |
, |
||
|
|||||
|
dt |
[(nkzu)2 −ωLe2 ]−1 ρbn , |
|
(35.1) |
|
ρn = ωLb2 |
n = 2,3,K . |
||||
Подставляя величины ρ2 , ρ3 и т.д. в уравнение для относительной скорости электронов пуч-
ка υ , преобразуем систему (34.14) к следующему виду:
2ikzu ddtρ + [(kzu)2 −ωLe2 ]ρ = ωLb2 ρb1, dydt = kzuυ,
kzu |
dυ |
+ |
1 |
iωLb2 |
γ −3 (1− 2β 2γ 2υ)3 2 ∑∞ 1 |
(gn ρbn exp(iny) −C.C.)= |
(35.2) |
dt |
2 |
|
|||||
|
|
|
n=1 n |
|
|
= − 12 iωLe2 γ −3 (1− 2β 2γ 2υ)3 2 (ρ exp(iy) −C.C.).
2 (ρ exp(iy) −C.C.).
Здесь ρ ≡ ρ1 - медленная амплитуда резонансной первой пространственной гармоники плаз-
менной волны, а
|
|
|
|
1 , |
|
|
|
|
|
|
n =1; |
|
||||||
gn = 1 +ω2 |
[(nk |
u)2 |
−ω2 |
]−1, n = 2,3,K . |
(35.3) |
|||||||||||||
|
|
|
Le |
z |
|
|
|
|
|
Le |
|
|
|
|
|
|
||
Введем безразмерные переменные |
|
|||||||||||||||||
τ = |
|
δω |
|
t, |
η = ωp |
|
δω |
|
−1υ, |
ε = −i2ωLe |
|
δω |
|
ωLb−2 ρ , |
(35.4) |
|||
|
|
|
|
|
|
|||||||||||||
где δω −инкремент (32.11) резонансной черенковской пучковой неустойчивости в плазме. Использование переменных (35.4) позволяет записать нелинейные уравнения (35.2) в виде, содержащем минимальное число свободных параметров. В линейном приближении эти переменные эквивалентны использованным при получении универсального дисперсионного уравнения (32.24). В безразмерных переменных уравнения (35.2) записываются в виде
160
