
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Глава VI. Предельные токи и динамика электронных пучков
всильном внешнем магнитном поле
§26. Предельный вакуумный ток
Вочень сильном внешнем магнитном поле электроны пучка движутся практически прямолинейно вдоль силовых линий магнитного поля, а поперечное движение электронов в основном заморожено. Внешнее магнитное поле будем считать сильным, если выполнено неравенство, противоположное (24.16), т.е.
|
|
z = Ωerb >>1 , или |
B >> |
I0 |
≡ B |
0 |
, |
|
|
(26.1) |
|
|
|
|
|
||||||
|
|
c |
0 |
rbc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где I |
0 |
- ток (16.1). При радиусе пучка |
r =1см имеем B |
0 |
≈ 0,17Т =1,7 103 |
Гс. В практике экс- |
||||
|
|
|
|
b |
|
|
|
|
||
периментальных исследований и технических разработок, связанных с релятивистскими сильноточными электронными пучками, такое магнитное поле вполне обычно.
Выполнения неравенства (26.1) еще недостаточно, чтобы в применении к конкретному электронному пучку внешнее магнитное поле можно было бы считать сильным - необходимы ограничения и на величину тока пучка. Пусть пучок находится в равновесии, т.е. имеет
место следующее (см. (24.11) и (24.14)): |
|
|
|
|
|
|||||||||||||
x < x |
max |
= |
1 |
γ |
0 |
z , или |
I |
b |
< |
1 |
|
u |
γ |
0 |
I |
0 |
z . |
(26.2) |
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
2 c |
|
|
|
|||||||||
Здесь u - продольная скорость пучка, γ0 |
= (1−u2 |
c2 )−1 2 . Будем предполагать, что неравенст- |
||||||||||||||||
во (26.2) является сильным. В состоянии равновесия пучок может иметь две угловые скоро-
сти вращения ω(+) и ω(−) , определенные при z >>1 в (24.19). Ранее было показано, что в ус-
ловиях (26.1) для вращения пучка на высокой частоте ω(+) требуется большая энергия элек-
тронов пучка, поскольку γ = γ0 |
1 + z2 >>1. Исключая этот экстремальный случай, считаем, |
|||||||||||||
что угловая скорость вращения пучка есть |
|
|
||||||||||||
ω(−) = |
c |
|
|
|
x |
= ω(+) |
|
x |
|
<< ω(+) < Ωe |
(26.3) |
|||
r γ |
|
|
γ |
|
γ |
|
z |
|||||||
|
0 |
|
0 |
z |
0 |
γ |
0 |
|
||||||
|
b |
|
|
|
|
|
|
|
|
|
||||
(при написании (26.3) учтены неравенство (26.1) и сильное неравенство (26.2)). При этом из
(24.20) имеем
|
|
|
x |
2 |
−1 2 |
|
γ |
|
− |
|
|
(26.4) |
|
= γ0 1 |
2 |
|
2 . |
|||
|
|
|
γ0 z |
|
|
|
Видно, что при выполнении сильного неравенства (26.2) угловая скорость вращения пучка не велика, а вклад вращательного движения в полную энергию электронов мал. Подводя итог, сформулируем условия, при которых внешнее магнитное поле является сильным:
111

Александров А.Ф., Кузелев М.В. Физика электронных пучков |
|
z >>1, x γ0 z <<1 . |
(26.5) |
Формально предполагаем, что выполнен предельный переход z → ∞. |
Соответствующее |
приближение называют приближением бесконечно сильного внешнего магнитного поля. В этом приближении электроны пучка полностью замагничены, т.е. движутся прямолинейно вдоль силовых линий внешнего магнитного поля (ω(−) → 0, γ → γ0 ). Заметим, что хотя не-
равенства (26.5) сформулированы на основании результатов § 24, где рассматривался тонкий пучок, они имеют смысл и для сплошного пучка, если под ∆b в (24.11) понимать rb .
Рассмотрим стационарную транспортировку полностью замагниченного электронного пучка в вакуумном дрейфовом пространстве, в которое пучок инжектируется после прохождения ускоряющего промежутка диода. В вакуумном пространстве дрейфа пучок электронов своим зарядом создает поле, препятствующее дальнейшей инжекции электронов в дрейфовое пространство. Поэтому существует некоторое максимальное значение тока пучка, выше которого стационарная транспортировка пучка через дрейфовое пространство вообще невозможна. Ситуация аналогична той, с которой мы столкнулись при выводе закона трех вторых в § 16. Разница в том, что в диоде имеется внешнее ускоряющее напряжение, а в пространстве дрейфа его нет.
Значение максимального тока бесконечно тонкого полностью замагниченного электронного пучка в цилиндрическом вакуумном пространстве дрейфа произвольного (т.е. не обязательно кругового) поперечного сечения определяется как условие разрешимости сле-
дующей стационарной системы уравнений: |
|
|
|
|
|
||||||||
∆ ϕ + ∂2ϕ |
= −4πen (z)S |
δ(rr |
− rr ),, |
|
|
|
|
|
|||||
|
∂z2 |
b |
b |
|
b |
|
|
|
|
|
|
|
|
nb (z)v(z) = n0bu = const, |
|
|
|
|
|
|
|
|
(26.6) |
||||
2 ~ |
2 |
γ = const. |
|
|
|
|
|
|
|
|
|||
mc |
γ (z) + eϕ = mc |
|
|
|
|
|
|
|
|
||||
Здесь ϕ(rr |
, z) - скалярный потенциал, ∆ |
|
- поперечная часть оператора Лапласа, S |
b |
- площадь |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
поперечного сечения пучка, |
rr |
- координата тонкого пучка в поперечном сечении, n |
0b |
- кон- |
|||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
центрация электронов пучка в плоскости инжекции (плоскость z = 0 ), |
nb (z) - концентрация |
||||||||||||
электронов в произвольном сечении z пространства дрейфа, u - скорость электрона пучка в плоскости инжекции, v(z) - скорость пучка в дрейфовом пространстве, γ = γ0 = (1−u2 c2 )−1 2 ,
γ~(z) = [1 − v(z)2 c2 ]−1 2 . При написании (26.6) предполагалось, что транспортировка пучка стационарная, а пространство дрейфа - металлическая труба произвольного поперечного сечения - расположено в области z > 0 . Первое уравнение в (26.6) есть уравнение Пуассона, второе – стационарное уравнение непрерывности, третье – стационарное уравнение Эйлера.
112

Александров А.Ф., Кузелев М.В. Физика электронных пучков
Очевидно, что |
ϕ(rr |
, z) |
и en (z) являются потенциалом собственного электростатического |
|||||||
|
|
|
|
|
|
|
|
|
b |
|
поля и плотностью собственного электрического заряда пучка. |
|
|||||||||
Уравнения (26.6) дополняются следующими граничными условиями: |
|
|||||||||
ϕ |
|
Σ = 0, |
ϕ |
|
z=0 |
= 0, |
ϕ |
|
z→∞ = const . |
(26.7) |
|
|
|
||||||||
|
|
|
|
|
||||||
Здесь Σ - металлическая боковая поверхность пространства дрейфа. Второе условие (26.7) означает, что в плоскости инжекции расположена металлическая фольга или сетка, прозрачная для инжектируемых электронов.
Решение стационарной задачи (26.6) – (26.7) существует, если только ток пучка меньше некоторого критического значения. Потенциал ϕ при больших z выходит на посто-
янную, а область изменения ϕ (там, где действует препятствующее инжекции пучка собст-
венное электрическое поле) локализована в непосредственной близости к плоскости инжек-
ции: 0 < z <~ R , где R - поперечный размер дрейфового пространства. При токах больших критического задача (26.6) – (26.7) решений не имеет, что означает невозможность стационарной транспортировки пучка с током, превышающим критический ток. Не вдаваясь в подробности решения полной задачи (26.6) – (26.7), определим лишь условие ее разрешимости, что и позволит получить выражение для критического тока пучка, называемого, по вполне
понятным причинам, предельным вакуумным током. |
|
|
|
|||
Предположим, что известны собственные функции ϕ |
n |
(rr |
) и собственные значения |
|||
|
|
|
|
|
|
|
k 2n следующей задачи на собственные значения: |
|
|
|
|||
|
= −k nϕn , |
|
|
|
||
∆ ϕn |
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
= 0. |
|
|
(26.8) |
ϕ |
|
|
|
|
|
|
n |
|
Σ=0 |
|
|
|
|
|
|
|
|
|
||
В случае дрейфового пространства в виде волновода кругового сечения ϕn |
= Jl (k n r) , где |
J l − функция Бесселя порядка l , k n = µl,n R , µl,n −корень функции Бесселя, |
l −азимуталь- |
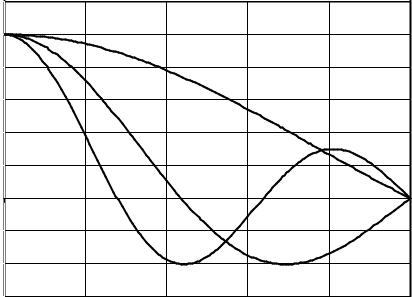
ное волновое число, а R − радиус волновода. На Рис. 26.1 для примера приведены три первые |
|
аксиально симметричные |
( l = 0 ) |
собственные |
цилиндрические функции J0 (µ0,n x) , где |
|||
x = r R (для справок: µ0,1 |
= 2,4048; |
µ0,2 = 5,5201; |
µ0,3 |
= 8,6537 ). |
||
Учитывая, что при z → ∞ потенциал ϕ(rr , z) |
не зависит от координаты z , разложим |
|||||
его в ряд по собственным функциям ϕ |
n |
(rr ) : |
|
|
||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
ϕ(rr ) = ∑Anϕn (rr ) . |
|
|
|
|
(26.9) |
|
n=1
Выражая из уравнения Пуассона постоянные коэффициенты An через плотность электронов пучка на бесконечности nb (∞) (при этом используется свойство ортогональности собствен-
113
Александров А.Ф., Кузелев М.В. Физика электронных пучков
1.2 |
|
|
|
|
|
1 |
|
|
|
|
|
0.8 |
|
n =1 |
|
|
|
|
|
|
|
|
|
0.6 |
|
n =2 |
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
n =3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
x1 |
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
|
-0.2 |
|
|
|
|
|
-0.4 |
|
|
|
|
|
-0.6 |
|
|
|
|
|
|
|
Рис. 26.1 |
|
|
|
|
|
Функции Бесселя J0 (µ0,n x) |
|
|
|
114

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ных функций) и исключая nb (∞) из второго и третьего уравнений системы (26.6), получим следующее соотношение:
|
|
|
|
|
|
|
ω2 |
∞ |
k 2 |
ϕ2 |
(rr ) |
= |
|
|
γ 3 |
3 2 [γ∞−2 (γ −γ∞ )2 |
(γ∞2 −1)] |
1 2 |
≡ F(γ∞ ) , |
(26.10) |
||
|
|
|
|
|
|
|
2 Lb2 Sb ∑ |
21 |
n |
b2 |
(γ |
2 |
−1) |
|
||||||||
|
|
|
|
|
|
|
k 1u |
n=1 |
k n ϕ2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
где γ∞ = γ~(∞) - |
релятивистский фактор электронов пучка, |
|
устанавливающийся при |
z → ∞ , |
||||||||||||||||||
|
|
|
|
ϕ |
n |
|
−норма, а ω |
Lb |
= |
4πe2n |
|
m − ленгмюровская частота электронов пучка. |
|
|||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0b |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
В левой части соотношения (26.10) находится величина, пропорциональная току пуч- |
|||||||||||||||
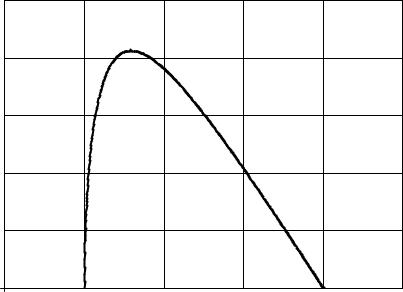
ка. Функция в правой части этого соотношения |
F(γ∞ ) |
обращается в нуль при |
γ∞ =1 и |
|||||||||||||||||||
γ∞ = γ , а в промежуточной точке |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
γ∞ = γ1 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(26.11) |
достигает максимума (Рис. 26.2). Вычисляя максимум функции F(γ∞ ) , получим максималь-
ное значение левой части соотношения (26.10), из которого и следует искомое выражение для предельного тока тонкого электронного пучка в вакуумном пространстве дрейфа. А именно:
I |
b0 |
= I |
0 |
(γ 2 3 |
−1)3 2 G , |
|
(26.12) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ 1 |
ϕ2 |
(rr ) −1 |
|
|||||||||||
Gb |
= |
4π∑ |
|
|
|
|
|
|
n |
|
|
|
|
b |
. |
(26.13) |
||
k |
2 |
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
= |
n |
|
|
|
|
ϕn |
|
|
|
|
|
|
||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
В случае дрейфового пространства в виде металлического волновода кругового поперечного сечения с радиусом R (пучок при этом является бесконечно тонким трубчатым с радиусом rb и толщиной ∆b , см. Рис. 16.2) геометрический фактор (26.13) вычисляется с ис-
пользованием формулы
1 |
∞ |
|
|
ln x = −∑J02 (µ0,n x)J1−2 (µ0,n )µ0−,2n , x ≤1 . |
(26.14) |
||
2 |
|||
n=1 |
|
В результате для предельного вакуумного тока тонкого трубчатого электронного пучка в круглом волноводе имеем выражение:
Ib0 = I0 |
(γ 2 3 −1)3 2 |
. |
(26.15) |
|
2ln R r |
||||
|
|
|
||
|
b |
|
|
Для пучка с γ = 2 , rb =1см при R = 2см из (26.15) получаем оценку Ib0 ≈ 5,5kA.
Если электронный пучок не является бесконечно тонким, а имеет конечный размер в поперечном сечении волновода, то аналитическое выражение для его предельного вакуумного тока найти сложно. Поэтому, в литературе получили распространение приближенные
115
Александров А.Ф., Кузелев М.В. Физика электронных пучков
2.5
F |
γ =4 |
2
1.5
1
0.5
γ ∞
0
0 |
1 |
2 |
3 |
4 |
5 |
Рис. 26.2
К определению предельного вакуумного тока тонкого пучка
116

Александров А.Ф., Кузелев М.В. Физика электронных пучков
формулы. В случае трубчатого пучка конечной толщины
Ib0 |
= I0 |
|
|
(γ 2 3 −1)3 2 |
|
. |
(26.16) |
∆ |
|
r + 2ln R r |
|||||
|
|
b |
|
|
|||
|
|
|
b |
b |
|
|
|
В случае сплошного цилиндрического пучка предельный ток оказывается следующим:
Ib0 |
= I0 |
(γ |
2 3 −1)3 2 |
. |
(26.17) |
1+ 2ln R r |
|||||
|
|
|
b |
|
|
И наконец, при полном заполнении волновода пучком из (26.17) имеем |
|
||||
Ib0 |
= I0 (γ 2 3 −1)3 2 . |
|
(26.18) |
||
Обратим внимание, что в сильно релятивистском случае, при γ >>1 и |
u ~ c , токи |
||||
(26.12), (26.15) – (26.18), а также токи (16.10) и (16.12), по порядку величины (с точностью до геометрического множителя) равны γI0 . Поскольку в вакуумном пространстве дрейфа ток пучка не может превосходить предельный вакуумный ток, то неравенство (26.2) оказывается следствием неравенства (26.1). Вернемся еще к условию (23.17), при выполнении которого тонкий трубчатый электронный пучок находится в равновесном состоянии. Для не нейтрали-
зованного ( f = 0 ) релятивистского пучка (23.17) сводится к неравенству Ib < γI0 z2 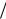 8 , более слабому, чем (26.2).
8 , более слабому, чем (26.2).
Итак, при токах пучка, превышающих предельный вакуумный ток, задача (26.6) – (26.7) решений не имеет. Это, конечно, не означает, что не имеет решений задача инжекции:
просто при Ib > Ib0 эти решения оказываются нестационарными. Как показывают компью-
терные и реальные эксперименты, при инжекции в пространство дрейфа пучка с током,
большим вакуумного, на расстоянии порядка R от плоскости инжекции формируется вир-
туальный катод. От него отражается часть инжектируемых электронов обратно в сторону плоскости инжекции. Проходящий же в глубь дрейфового пространства ток в среднем оказывается порядка предельного вакуумного. Формирование и динамика виртуального катода подробно будут исследованы в дальнейшем на примере неустойчивости Пирса. Предварительно целесообразно рассмотреть волны плотности заряда в электронных пучках.
§ 27. Волны плотности заряда в одномерном пучке электронов
Рассмотрим поперечно безграничный, однородный, нейтрализованный электронный пучок, движущийся с постоянной скоростью u в направлении оси OZ вдоль сильного внешнего магнитного поля. Движение тяжелых ионов, обеспечивающих зарядовую нейтрализацию пучка, не учитываем. В состоянии равновесия в нейтрализованном по заряду пучке собственное электрическое поле отсутствует. Исследуем продольные потенциальные возму-
117
Александров А.Ф., Кузелев М.В. Физика электронных пучков
щения равновесного состояния пучка, зависящие только от координаты z . Гидродинамические скорость, плотность и электромагнитное поле представим в виде:
V |
|
|
|
|
|
~ |
(z,t)}, |
|||
|
(z,t) = {0,0,u +V |
|||||||||
b |
|
(z,t) = n |
|
~ |
|
bz |
|
|
(27.1) |
|
N |
|
|
|
+ N |
|
(z,t), |
||||
rb |
|
0b |
~ |
b |
|
|
r |
|
||
~ |
|
|
|
|
|
|
|
~ |
= 0. |
|
E |
(z,t) = {0,0, Ez (z,t)}, |
B |
||||||||
Здесь возмущенные величины помечены знаком “~”. Ограничиваясь случаем нерелятивистского пучка и линейным по возмущениям приближением, уравнения гидродинамики (18.7),
(18.9) и соотношения (18.10) записываем следующим образом: |
|
||||||||||||||
~ |
|
~ |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
∂Nb |
+ u |
∂Nb |
|
= −n |
∂Vbz |
, |
|
|
|||||||
∂t |
|
∂z |
|
|
|
|
|
|
|
0b |
∂z |
|
|
|
|
~ |
|
~ |
|
|
|
|
|
|
e ~ |
|
|
|
|
||
∂Vbz |
|
∂Vbz |
|
|
|
|
|
|
|
|
|
|
|||
∂t |
+ u |
∂z |
= |
|
Ez , |
|
|
(27.2) |
|||||||
m |
|
|
|||||||||||||
~ |
|
~ |
|
|
|
|
~ |
|
~ |
~ |
|
|
|||
jb = e(n0bVbz |
+ uNb ), |
ρb |
= eNb . |
|
|||||||||||
Для возмущений в виде плоских волн |
|
||||||||||||||
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(27.3) |
Ez = Ez (ω,kz )exp(−iωt +ikz z), |
|||||||||||||||
где ω - частота, kz - продольное волновое число, из (27.2) имеем |
|
||||||||||||||
~ |
|
|
|
|
e |
|
|
|
|
|
−1 ~ |
|
|
||
Vbz (ω, kz |
)= i |
|
|
|
|
|
(ω − kzu) |
Ez (ω, kz ), |
|
||||||
|
m |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
~ |
|
|
|
|
e |
|
|
|
|
|
|
−2 ~ |
|
||
Nb (ω, kz )= i |
|
|
n0bkz (ω − kzu) |
Ez (ω, kz ), |
(27.4) |
||||||||||
m |
|||||||||||||||
~ |
|
|
i |
|
2 |
|
|
−2 |
~ |
|
|||||
jb (ω, kz )= |
|
|
ωb ω(ω − kzu) |
Ez (ω, kz ). |
|
||||||||||
4π |
|
||||||||||||||
Из последнего соотношения (27.4) и линеаризованных материальных уравнений (19.9) и (19.12) следуют выражения для комплексных продольных проводимости и диэлектрической проницаемости пучка
σ l (ω, k |
|
)= |
|
i |
|
|
ωωLb2 |
|
, |
|
z |
|
4π (ω − kzu )2 |
||||||||
|
|
|
|
(27.5) |
||||||
|
|
|
|
|
|
|
|
ωLb2 |
|
|
ε l (ω, k |
|
|
)= |
1 − |
|
|
. |
|
||
z |
(ω − kz u)2 |
|
||||||||
|
|
|
|
|
|
|||||
Заметим, что у пучка проводимость и диэлектрическая проницаемость являются тензорами. В сильном внешнем магнитном поле структура этих тензоров достаточно проста: в тензоре проводимости σzz = σ l , в тензоре диэлектрической проницаемости εzz = εl , εxx = εyy =1, а
другие компоненты обоих тензоров равны нулю.
|
r |
~ |
|
|
|
|
~ |
с учетом (27.3) и второго выражения (27.4) сво- |
|||
Уравнение Максвелла divE |
= 4πρb |
||||
дится к алгебраическому соотношению kzε |
l |
~ |
|||
|
(ω, kz )Ez (ω, kz ) = 0 . Откуда для нетривиальных |
||||
~ |
(ω, kz ) ≠ 0 , следует дисперсионное уравнение для спектров час- |
||||
решений (27.4), в которых Ez |
|||||
|
|
|
|
118 |
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков
тот продольных волн рассматриваемого пучка электронов
εl (ω, k |
|
) =1 − |
ω2 |
= 0. |
(27.6) |
|
|
Lb |
|||||
z |
(ω − kzu)2 |
|||||
|
|
|
|
|||
Из (27.6) находим спектры частот двух волн плотности заряда |
|
|||||
ω = kzu ±ωLb . |
|
|
(27.7) |
|||
Волна, дисперсия которой описывается формулой (27.7) со знаком плюс, получила название быстрой волны. Волна, в законе дисперсии которой взят знак минус, называется медленной (полагаем, что ω > 0 ; при изменении знака частоты указанные волны меняются местами). В движущейся вместе с электронным пучком системе координат с учетом доплеровского пре-
образования частоты спектры (27.7) переходят в ω = ±ωLb , т.е. трансформируются в спектры обычных продольных волн электронной плазмы с ленгмюровской частотой ωLe = ωLb .
Медленная волна (27.7) обладает интересным и необычным свойством, обусловливающим ее исключительно важную роль в физике электронных пучков и их приложениях. Для более подробного исследования свойств волн (27.7) рассмотрим изменение плотности энергии пучка при возбуждении в нем этих волн. Изменение плотности энергии складывается из плотности энергии электрического поля
|
|
~2 |
|
|
|
|
|
|
|
|
||
WE |
= |
Ez |
|
|
|
|
|
|
|
|
(27.8) |
|
8π |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
и изменения плотности кинетической энергии |
|
|||||||||||
|
|
m |
~ |
~ 2 |
|
m |
|
2 |
|
|
||
WK |
= |
|
|
(n0b + Nb )(u +Vb ) |
− |
|
n0bu |
|
. |
(27.9) |
||
2 |
|
2 |
|
|||||||||
В линейной теории энергетические характеристики вычисляются с точностью до квадратичных по возмущениям величин, что применительно к (27.9) дает
|
m ~ |
2 |
~ |
~ ~ |
~2 |
|
|
|
WK = |
|
(Nbu |
|
+ 2un0bVb + 2uNbVb + n0bVb |
). |
(27.10) |
||
2 |
|
|||||||
При вычислении квадратичных по возмущениям величин следует учитывать, что операция возведения в квадрат является нелинейной, поэтому вместо комплексной величины (27.3) следует использовать ее действительную часть равную
~ |
1 |
~ |
~ |
|
|
Ez = |
|
[Ez |
(ω,kz )exp(−iωt +ikz z)+ Ez |
(ω,kz )exp(iωt −ikz z)], |
(27.11) |
2 |
где символом “звездочка” обозначена операция комплексного сопряжения. Кроме того, нужно иметь в виду, что сами возмущения и квадратичные по ним величины содержат быстро осциллирующие составляющие. Поэтому энергетические характеристики должны быть ус-
реднены по периоду T = 2π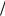 ω . Таким образом, полное изменение плотности энергии пучка вычисляется по формуле
ω . Таким образом, полное изменение плотности энергии пучка вычисляется по формуле
119
Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
T |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
1 |
|
|
T (W |
+W )dt . |
|
|
|
|
|
|
|
(27.12) |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
E |
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя в (27.12) последовательно выражения (27.8), (27.10), (27.3) и (27.11), по- |
|||||||||||||||||||||
сле несложных преобразований окончательно получим |
|
||||||||||||||||||||
|
|
|
|
ω |
2 |
(ω + k |
u) |
|
~ |
|
2 |
|
|
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
Ez (ω, kz ) |
|
|
|
|
||||||||||
W = 1 |
+ |
|
|
Lb |
z |
|
|
|
|
|
|
|
|
|
. |
(27.13) |
|||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
(ω − kzu)3 |
|
|
|
16π |
|
|
|
|||||||||
Отсюда с учетом законов дисперсии (27.7) имеем |
|
||||||||||||||||||||
|
|
|
|
ω |
|
|
|
|
~ |
) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
W = ± |
|
|
|
|
|
|
Ez (ω, kz |
|
|
, |
|
|
|
|
|
|
(27.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ωLb |
|
|
|
8π |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где, как и в (27.7), знак плюс относится к быстрой волне, знак минус – к медленной, а ω > 0 . Из (27.14) следует, что изменение плотности энергии пучка при возбуждении в нем медленной волны отрицательно. На этом основании медленную волну принято называть волной с отрицательной энергией. Отрицательность энергии означает, что имеющаяся в невозмущенном пучке энергия при возбуждении в нем медленной волны уменьшается. Другими словами при возбуждении медленной волны выделяется энергия, которая может пойти на возбуждение какой-либо другой системы. Именно это свойство волн с отрицательной энер-
гией делает их принципиально важными для многочисленных приложений.
Энергия быстрой волны, как видно из (27.14), положительна, т.е. для возбуждения такой волны требуется вклад энергии извне. В случае обычной плазмы, т.е. электронного пучка с нулевой скоростью, из (27.13) при u = 0 следует выражение для плотности энергии про-
дольных волн электронной плазмы (ωLe = ωLb )
|
|
ω |
2 |
|
|
~ |
|
2 |
|
~ |
|
2 |
|
|
||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Ez (ω, kz ) |
|
|
|
|
|
Ez (ω, kz ) |
|
|
|
|
||||
|
|
|
Le |
|
|
|
|
|
|
|
|
|
|
|
|
(27.15) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
|
|
|
|
|
= |
|
|
|
|
. |
|||||||
W = 1 |
ω |
2 |
|
|
16π |
|
|
8π |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Последняя величина, как это и должно быть, всегда положительна. Действительно, изменение энергии системы, имеющей в невозмущенном состоянии нулевой запас энергии, может быть только большим нуля.
Вычислим теперь изменение плотности импульса пучка при возбуждении в нем волн плотности заряда
P = m(n0b + Nb )(u +Vb )− mn0bu = muNb + mn0bVb + mNbVb . |
(27.16) |
||||
~ |
~ |
~ |
~ |
~ ~ |
|
После подстановки соответствующих величин и усреднения по времени из (27.16) имеем:
|
2 |
|
|
|
~ |
|
2 |
|
kz |
|
|
~ |
|
2 |
|
kz |
|
||
|
|
|
|
|
|
|
|||||||||||||
P = |
kzωLb |
|
|
|
Ez (ω, kz ) |
|
|
|
|
|
|
Ez (ω, kz ) |
|
|
|
|
|||
|
|
|
|
|
|
|
= ± |
|
|
|
|
|
|
|
= |
|
W . |
(27.17) |
|
(ω − kzu)3 |
|
|
|
8π |
|
ωLb2 |
|
|
|
8π |
|
ω |
|||||||
Связь (27.17) между P и W есть частный случай общего соотношения
120
