
ASVT Материалы / Лекции / ЭЛТ / 27_VaN[1]
.pdf
|
|
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков |
||||||
|
dε |
~ |
|
|
|
|
|
|
|
|||
|
|
|
−i∆ε = −ρb1, |
|
|
|
|
|
|
|||
|
dτ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
=η, |
|
|
|
|
|
. |
(35.5) |
||
|
dτ |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dη |
1 |
|
3 2 |
1 3 |
|
1 |
3 2 |
|
|
||
|
|
|
+ |
|
i(1 |
− µη) ν |
|
= 2 |
(1− µη) |
(ε exp(iy)+ С.C.). |
|
|
|
dτ |
|
2 |
|
|
|||||||
Здесь ν - |
параметр (32.19), |
- |
безразмерная сумма по n |
из третьего уравнения системы |
||||||||
~ |
|
|
|
−1 3 |
- расстройка в уравнении (32.24), ∆- приведена в (32.18), а µ −важный па- |
|||||||
(35.2), ∆ = ∆ν |
|
|||||||||||
раметр релятивизма электронного пучка при резонансной пучковой неустойчивости в плазме, определяемый формулой
|
2 |
|
2 |
δω |
|
2 |
|
|
ω2 |
γ −3 |
1 3 |
|
2 |
2 1 3 |
|
2 |
|
1 3 |
|
|
µ = 2β |
γ |
|
= 2β |
γ |
2 |
Lb |
|
|
|
|
|
. |
(35.6) |
|||||||
|
|
kzu |
|
|
2ωLe2 |
|
= 2β |
|
γ ν |
= 2(γ |
|
−1)ν |
|
|||||||
Учитывая теперь неравенство (32.5), т.е. ν <<1 , пренебрежем членом с суммой в третьем уравнении системы (35.5) и получим окончательно следующую систему уравнений, описывающих нелинейную динамику резонансной черенковской неустойчивости релятивистского электронного пучка в плазме:
dε |
~ |
|
|
|
1 |
2π |
|||
|
|
−i∆ε |
= −ρb , |
ρb = |
|
∫0 exp(−iy)dy0 , |
|||
dτ |
π |
||||||||
dy |
|
=η, |
|
|
|
|
(35.7) |
||
dτ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
dη |
1 |
|
|
3 2 |
|
|
|
||
|
|
= |
|
|
(1 |
− µη) |
(ε exp(iy)+ С.C.). |
||
dτ |
|
2 |
|||||||
Здесь ρb ≡ ρb1 - амплитуда резонансной гармоники волны плотности заряда пучка. Видно,
что высшие гармоники ρbn , n = 2,3,K, при ν <<1 на нелинейную динамику резонансной не-
устойчивости не влияют. Приведем еще явный вид критерия применимости линейного приближения для описания плазмы при резонансной неустойчивости. Для этого в общее условие (34.10) подставим инкремент (32.11), что дает
ωLb2 γ 3 2 << ωLe2 . |
(35.8) |
Последнее неравенство является более жестким, чем (32.5). |
|
В линейном приближении ε ~ exp(−iδ~τ) |
и из системы (35.7) следует универсальное |
дисперсионное уравнение (32.24) для “абсолютного” комплексного безразмерного инкремен-
та δ~ . Надо отметить, что абсолютный (или универсальный) характер имеет и система урав-
нений (35.7), поскольку зависит всего только от двух параметров ∆~ и µ . А при ∆~ = 0 и
µ → 0 , т.е. в условиях точного черенковского резонанса и для нерелятивистского пучка,
система (35.7) вообще не содержит никаких параметров. Заметим так же, что случай нереля-
161

Александров А.Ф., Кузелев М.В. Физика электронных пучков
тивистского пучка при резонансной черенковской неустойчивости означает выполнение не-
равенства µ <<1, а отнюдь не сводится только к условию β 2 <<1 . Так, нелинейная динами-
ка пучка очень малой плотности, если выполнено неравенство µ <<1, будет нерелятивист-
ской, даже если у этого пучка β ~ 1 и γ >>1 . Тем самым, релятивизм, или его отсутствие оп-
ределяются не только энергией электронов пучка, но и его плотностью.
Вводя безразмерный «импульс» электрона пучка |
|
||||||||||||
|
p = (1− µη)−1 2 , |
|
|
|
|
|
|
(35.9) |
|||||
запишем уравнения (35.7) в следующем эквивалентном виде |
|
||||||||||||
|
dε |
~ |
|
|
|
|
1 |
2π |
|
|
|
|
|
|
|
−i∆ε = −ρb |
, ρb = |
|
∫0 exp(−iy)dy0 , |
|
|||||||
|
dτ |
π |
|
||||||||||
|
dy |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
= |
1− |
, |
|
|
|
|
. |
(35.10) |
||||
|
|
|
|
2 |
|
|
|
|
|||||
|
dτ |
µ |
|
p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
dp |
= µ |
(ε exp(iy) + С.C.), p |
|
=1. |
|
|||||||
|
|
|
|||||||||||
|
dτ |
|
|||||||||||
|
4 |
|
|
|
|
|
|
|
τ =0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения типа (35.10) в дальнейшем будут использованы для оценки эффективности резонансного пучково-плазменного взаимодействия. Заметим, что величина (35.9) импульсом электрона пучка, вообще говоря, не является. Но при выполнении неравенства (34.13) она пропорциональна импульсу как при µ <<1, так и в противоположном пределе.
В общем случае уравнения (35.7) или (35.10) решаются только численно, но универсальный характер этих уравнений ставит их численные решения на уровень аналитических. Дополним систему (35.7) следующими начальными условиями:
ε(τ = 0) = ε0 , y(τ = 0) = y0 + b sin y0 , υ(τ = 0) = 0 , |
(35.11) |
где ε0 - начальная амплитуда плазменной волны, а b - задает глубину начальной модуляции пучка по плотности (легко показать, что при | b | <<1 имеем | ρb | = | b | ). Зададимся конкрет-
ными параметрами ε0 =10−3 , b = 0 , ∆~ = 0 и рассмотрим результаты численного решения уравнений (35.7).
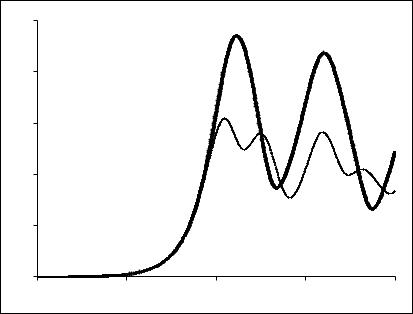
На Рис. 35.1 изображены амплитуды ε(τ) и ρb (τ) , полученные решением уравнений
(35.7) для нерелятивистского случая, т.е. при µ = 0 . На начальном этапе обе величины на-
растают по экспоненте как exp ( 3τ 2) , что согласуется с линейной теорией. В дальнейшем происходит нелинейная стабилизация неустойчивости. После стабилизации амплитуда ε(τ)
производит регулярные колебания между некоторыми максимальным и минимальным уровнями. Это обусловлено захватом электронов пучка полем плазменной волны. На каждой длине плазменной волны электроны пучка формируют сгусток, который совершает колеба-
162
Александров А.Ф., Кузелев М.В. Физика электронных пучков
2.5 |
|ε |, |ρ b | |
|
|
|
2 |
|
|
|
|
1.5 |
|
|
|
|
1 |
|
|
|
|
0.5 |
|
|
|
|
0 |
|
|
|
τ |
|
|
|
|
|
0 |
5 |
10 |
15 |
20 |
Рис. 35.1
Динамика амплитуд | ε | и | ρb | при резонансной черенковской неустойчивости нерелятивистского электронного пучка в плазме
163

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ния между горбами потенциала плазменной волны, то отдавая ей энергию, то отбирая обратно. Поскольку за одно колебание сгусток дважды сталкивается с потенциальными горбами – один раз с передним, другой раз с задним – осцилляции амплитуды ρb (τ) происходят вдвое
чаще, чем у ε(τ) .
Из Рис. 35.1 следует, что максимальное значение амплитуды ε(τ) ≈ 2,34 ≡ | ε |max , то есть порядка единицы. Отсюда и из определения безразмерных величин (35.4) имеем оценку для максимальной амплитуды безразмерного возмущения плотности плазмы
ρ |
|
= |
| ε | |
|
ω2 |
|
ω2 |
|
2 3 |
(35.12) |
|
|
max |
b |
≈ γ 3 2 |
b |
|
. |
|||
|
max |
|
2 |
ωp | δω | |
|
ωp |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
В соответствии с неравенством (35.8) величина (35.12) мала и, следовательно, предположение о возможности линейного описания плазмы вполне оправдано. Что касается электронно-
го пучка, то как видно из Рис. 35.1, ρb max ≈1 , т. е. пучок малой плотности при резонансной неустойчивости в плазме модулируется полностью.
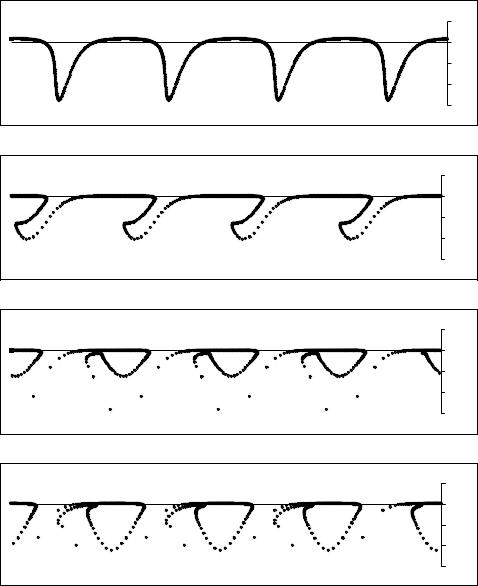
На Рис. 35.2 для некоторых моментов времени τ представлены фазовые плоскости электронов нерелятивистского пучка при резонансной неустойчивости в плазме: по горизонтали отложены безразмерные координаты электронов y( y0 ,τ) , по вертикали – безразмерные относительные скорости η( y0 ,τ) . Рис. 35.2 соответствует предыдущему Рис. 35.1 и иллюст-
рирует динамику формирования и эволюции сгустка электронов пучка при его захвате излучаемой плазменной волной. Этот процесс называют бунчировкой пучка полем волны. Заметим, что при захвате формируются встречные потоки электронов пучка, что может быть описано только в рамках модели кинетического уравнения Власова.
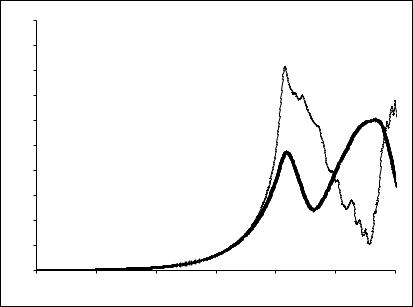
На Рис. 35.3 изображены амплитуды ε(τ) и ρb (τ) , полученные численным решением уравнений (35.7) в релятивистском случае при µ = 4 . На следующем Рис. 35.4 для того же параметра релятивизма µ приведены фазовые плоскости электронов пучка. Как и в нереля-
тивистском случае, система (35.7) описывает насыщение резонансной пучковой неустойчивости за счет захвата электронов пучка резонансной плазменной волной, что в первую очередь видно из структуры фазовых плоскостей. Релятивизм, конечно, привносит особенности в процесс бунчировки пучка, динамику осцилляций амплитуд после захвата и уровни их насыщения. На Рис. 35.5 представлены зависимости от параметра релятивизма µ амплитуды насыщения плазменной волны | ε |max и времени стабилизации резонансной неустойчивости
τ0 . Время стабилизации определялось по моменту достижения амплитудой ρb (τ) своего первого максимума.
164
Александров А.Ф., Кузелев М.В. Физика электронных пучков
165

Александров А.Ф., Кузелев М.В. Физика электронных пучков
τ =9 |
1 |
|
0 |
|
-1 |
τ =11 |
3 |
|
2 |
|
1 |
|
0 |
|
-1 |
|
-2 |
|
-3 |
τ =13 |
4 |
|
2 |
|
0 |
|
-2 |
|
-4 |
τ =15 |
4 |
|
2 |
|
0 |
|
-2 |
|
-4 |
Рис. 35.2
Фазовые плоскости электронов нерелятивистского пучка при резонансной черенковской неустойчивости
166
Александров А.Ф., Кузелев М.В. Физика электронных пучков
1 |
|ε |, |ρ b | |
|
|
|
|
|
0.9 |
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
0.1 |
|
|
|
|
|
τ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
Рис. 35.3
Динамика амплитуд | ε | и | ρb | при резонансной черенковской неустойчивости релятивистского электронного пучка в плазме ( µ = 4 )
167
Александров А.Ф., Кузелев М.В. Физика электронных пучков
τ=8
τ=8,3
1
0 -1 -2 -3
10
0 -10 -20 -30
τ =8,6 |
10 |
|
0 |
|
-10 |
|
-20 |
|
-30 |
τ =9 |
5 |
|
0 |
|
-5 |
|
-10 |
|
-15 |
Рис. 35.4
Фазовые плоскости электронов релятивистского пучка ( µ = 4 ) при резонансной черенковской неустойчивости
168

Александров А.Ф., Кузелев М.В. Физика электронных пучков
2.5 |
|ε max | |
|
|
|
|
2 |
|
|
|
|
|
1.5 |
|
|
|
|
|
1 |
|
|
|
|
|
0.5 |
|
|
|
|
|
0 |
|
|
|
|
µ |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
12 |
τ 0 |
|
|
|
|
10 |
|
|
|
|
|
8 |
|
|
|
|
|
6 |
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
µ |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
Рис. 35.5
Амплитуда насыщения | εmax | и время стабилизации τ0 резонансной черенковской неустойчивости в зависимости от параметра релятивизма пучка µ
169
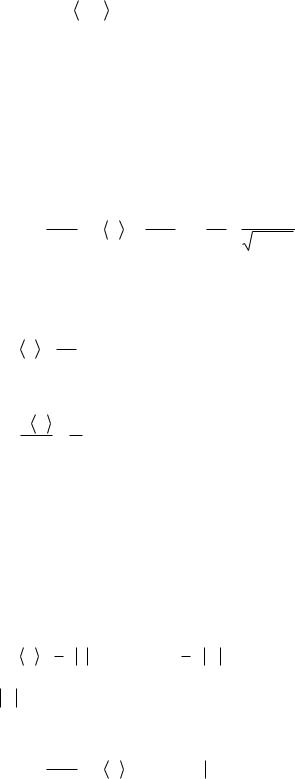
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Таким образом, при развитии резонансной черенковской пучковой неустойчивости в плазме происходит возбуждение интенсивных плазменных колебаний, о чем, в частности, свидетельствуют результаты численных расчетов, представленные на Рис. 35.1 и 35.3.
Определим эффективность пучково-плазменного взаимодействия как относительное изменение средней кинетической энергии электронов пучка
Ε = |
(γ − |
γ (t) ) |
, |
(35.13) |
|
(γ |
−1) |
|
|||
где γ (t) −релятивистский фактор электрона в момент t , а угловые скобки означают усредне-
ние по всем электронам, приходящимся на длину резонансной плазменной волны 2π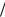 kz . Ве-
kz . Ве-
личина (35.13) задает долю кинетической энергии пучка, передаваемой плазменным колебаниям при резонансной неустойчивости. Выражая скорость электрона через безразмерную величину η (см. формулы (34.13) и (35.6)), преобразуем (35.13) к виду
|
|
γ |
(1 − p )= |
γ |
|
1 |
2π |
dy0 |
|
|
Ε = |
|
1 − |
∫ |
, |
(35.14) |
|||||
|
γ −1 |
|
γ −1 |
|
2π |
0 |
1 − µη |
|
||
где величина p определена в |
(35.9). Применим теперь к обеим частям последнего уравнения |
|||||||||
системы (35.10) оператор усреднения по длине волны |
|
|||||||||
... = |
1 |
2π(...)dy0 . |
|
|
|
|
|
|
(35.15) |
|
|
|
2π |
∫0 |
|
|
|
|
|
|
|
В результате получим |
|
|
|
|
|
|
|
|||
d p |
|
= µ (ερ + ε |
ρ), |
|
|
|
|
|
(35.16) |
|
dτ |
|
8 |
|
|
|
|
|
|
|
|
где звездочкой обозначена операция комплексного сопряжения. Умножая далее первое урав-
нение в (35.10) на ε и складывая результат с комплексно сопряженным уравнением (35.10) умноженным на ε , получим
|
d |
|
ε |
|
2 |
= −(ερ +ε ρ). |
|
|
|
(35.17) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
dτ |
|
|
|
||||||
|
|
|
|
|
|
|||||
Сравнивая правые части (35.17) и (35.16), получаем первый интеграл уравнений (35.10) |
||||||||||
|
p + |
1 µ ε 2 = const =1 + |
1 |
µ ε0 |
2 , |
(35.18) |
||||
|
|
|
|
|
|
8 |
8 |
|
|
|
где ε0 −затравочная (при τ = 0 ) амплитуда плазменной волны. Из (35.18) следует оконча-
тельное выражение для эффективности пучково-плазменного взаимодействия (35.14)
Ε = |
γ |
(1 − p )= |
1 |
|
γ |
|
µ( |
ε |
|
2 − |
|
ε0 |
|
2 ). |
(35.19) |
|
|
|
|
||||||||||||
γ −1 |
8 |
|
γ −1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
В нерелятивистском случае, при β 2 <<1 , эффективность (35.19) оказывается следующей
170
