27_VaN[1]

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

Аппаратные средства вычислительной техники

Файл:

iν0 (1− 2β 2γ 2υ)3 2

qn [ρbn exp(iny) −С.C.].

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

4.53 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2918 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Ε = 1	2	1 3	(ε 2 − ε		2 )≈ 2,2(ω2	ω2 )1 3 .	(35.20)
Ε = 1	ωb		(ε 2 − ε	0	2 )≈ 2,2(ω2	ω2 )1 3 .	(35.20)
2	2			0	b	p
2	2ωp
При получении приближенного равенства в (35.20) было учтено, что ε0							<<1, а вместо \| ε \|

подставлено его максимальное значение | ε |max ≈ 2,34 , взятое из нерелятивистского числен-

ного расчета (см. Рис. 35.1).

В общем случае эффективность (35.19) можно рассчитать только численно. Она зависит от двух параметров γ и µ . Но сами уравнения (35.10) содержат только параметр реляти-

визма					~
	µ (при нулевой расстройке ∆). Поэтому величина
	Ε′ =	1	µ	εmax		2	(35.21)


	8						µ , и полностью
имеет некоторое универсальное значение, зависящее только от параметра

определяет по формуле (35.19) эффективность резонансного черенковского пучково-

плазменного взаимодействия. При этом εmax −максимальная (захватная) амплитуда, вычис-

ленная при ε0 → 0 . Эта амплитуда, представленная на Рис. 35.5, позволяет рассчитать и ве-

личину (35.21) – Рис. 35.6. Из последнего рисунка следует, что до 20% кинетической энергии пучка может быть преобразовано при резонансной черенковской неустойчивости в энергию плазменных колебаний.

Рассмотрим еще очень коротко, практически на уровне формулировки, описание нелинейной динамики апериодической нерезонансной пучковой неустойчивости в плазме. По-

лагая, что для всех целых n выполнено неравенство
\| (nkzu)2 −ωLe2 \| >> \| δω \|2 ,		(35.22)
где δω - резонансный инкремент (32.11), из уравнений (34.14) находим
	ω2	(35.23)
ρn = (nkzu)2 −ωLe2 ρbn , n =1,2,K.
	Lb

Подставляя далее выражения (35.23) в последнее уравнение системы (34.14), получим следующую систему уравнений:

Здесь использованы следующие переменные и обозначения:

τ′ = kzut, ν0 =	ωLb2 γ −3	n2
τ′ = kzut, ν0 =	kz2u2	, qn = n2 −ωLe2 kz2u2 .	(35.25)

171

Александров А.Ф., Кузелев М.В. Физика электронных пучков

0.2	E'
0.16
0.12
0.08
0.04
0					µ
0
0	1	2	3	4	5

Рис. 35.6

Эффективность пучково-плазменного взаимодействия при резонансной черенковской неустойчивости

172

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Начальные условия для уравнений (35.24) могут быть выбраны в виде
y	t=0 = y0 + ∑bn sin(ny0 +ςn ), υ	t=0 = 0 ,	(35.26)

	n

где bn и ςn - постоянные. Условия (35.26) описывают начальную модуляцию плотности пуч-

ка на всех пространственных гармониках. Впрочем, какие-то из bn можно задать нулевыми.

При апериодической неустойчивости нет параметра, позволяющего ограничить число пространственных гармоник в уравнениях (35.24). Не обсуждая здесь результатов численного моделирования апериодической неустойчивости, укажем только, что она приводит к полной модуляции пучка по плотности, т.е. для большого числа гармоник становится | ρbn | ≈1.

§ 36. Нелинейные равновесные состояния замодулированного электронного пучка в плазме

Предположим, что электрическое поле в пучково-плазменной системе имеет следую-

щую структуру:
Ez (t, z) = −	∂ϕ	= E0 sin(ω0t − kz0 z),		ω0 = u,

	∂z			kz0
ϕ(t, z) =ϕ0 cos(ω0t − kz0 z),			ϕ0 = −	E0	,

				kz0
где ω0 , kz0 и E0 -	постоянные.		Для определенности считаем, что

(36.1)

E0 < 0 (заряд электрона

e < 0 ). Найдем такое состояние электронного пучка, при котором он является совокупностью отдельных, не обменивающихся между собой частицами сгустков, локализованных около максимумов потенциала поля (36.1), т.е. около точек, определяемых соотношениями

z = ut + s	2π	, s = 0, ±1, ± 2,K.	(36.2)

	kz0

В соответствии со сделанным предположением решение характеристической системы кинетического уравнения (33.1) для функции распределения электронов пучка

= v,

dv =

e (1− v2

c2 )3 2 Ez (t, z)

следует искать в виде

2π

z = ut + s

kz0

+ z

, v = u + v .

Подставляя (36.4) в (36.3) получим следующие уравнения для возмущений

и v :

−3

2 ~

3 2

E0 (1 − 2β

= v ,

dt = − m γ

v u)

sin(kz0 z ) ,

где γ = (1 − u2

c2 )−1 2 .

(36.3)

(36.4)

(36.5)

173

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Предположим, что колебания электронов пучка около максимумов потенциала поля (36.1) являются малыми и нерелятивистским, т.е. имеют место неравенства

| kz0 ~z | <<1, γ 2 | v~u | <<1. (36.6)

Записывая с учетом (36.6) решение уравнений (36.5) и подставляя его в (36.4), получим следующее решение характеристической системы (36.3):

z = ut + s	2π	+ C cos Ωt + C	2	sin Ωt,

	1			(36.7)
	kz0

v = u −C1Ωsin Ωt + C2Ωcos Ωt.

Здесь
Ω2 = kz0γ −3 (eE0 m)-	(36.8)

квадрат частоты осцилляций электронов пучка в потенциальных ямах волны, а C1,2 - посто-

янные (поскольку было положено E0 < 0 , и e < 0 , тоΩ2 > 0 ).

Искомое решение кинетического уравнения (33.1) является произвольной функцией постоянных интегрирования C1 и C2 , т.е. fb (t, z, v) = f0 (C1 ,C2 ) , где С1,2 должны быть выра-

жены из решений (36.7) как функции t, z и v . Для удобства в качестве одного из независи-

мых аргументов функции распределения мы выбрали вместо импульса p скорость электро-

на v . Из (36.7) имеем

		2π			1
C1						(v −u) sin Ωt,

	= z −ut − s	kz0		cos Ωt −	Ω

			2π		1
C2						(v −u) cos Ωt,

	= z −ut − s		kz0	sin Ωt +	Ω

откуда следует соотношение

2	2		2π	2		1		2

C1	+ C2				+		2 (v − u) .
C1	+ C2	= z − ut − s	kz0		+	Ω	2 (v − u) .
			kz0			Ω

(36.9)

(36.10)

Учитывая простоту структуры выражения (36.10), функцию распределения электронов пучка зададим в виде fb (t, z, v) = f0 (C1 + C2 ) . В частности можно выбрать следующее распределе-

ние:

(t, z, v) = N

exp

−

Ω2 (C2

+ C 2 ) .

(36.11)

2κTb

Здесь Tb - температура электронов пучка,

κ - постоянная Больцмана, а постоянная N0 опре-

деляется из условия нормировки

N0 ∫∫ f0 (t, z, v)dzdv =

2π

n0b .

(36.12)

kz0

174

Александров А.Ф., Кузелев М.В. Физика электронных пучков

Очевидно, что величина (36.12) определяет полное число электронов в одном электронном сгустке.

Найденное распределение (36.11) относится к одному электронному сгустку. Для того чтобы получить полную функцию распределения электронов пучка, необходимо выражение (36.11) просуммировать по s , т.е. по всем электронным сгусткам. Окончательно после вы-

числения нормировочной постоянной N0

получим

mΩ

2 s=∞

2π

fb (t, z, v) = n0b

exp −

−u) ∑exp−

Ω

(36.13)

κT k

2κT

z −ut − s

s=−∞

Из координатной части распределения (36.13), представляющей распределение Больцмана для газа осцилляторов, находим условие выполнимости первого неравенства (36.6), а именно

eE0	3
	>> γ κT	,	(36.14)
	>> γ κT	,	(36.14)
kz0	b
kz0

т.е. глубина потенциальных ям поля с учетом релятивизма электронов должна быть больше, чем кинетическая энергия теплового движения электронов сгустка. При этом отсутствует, точнее, экспоненциально мал, обмен сгустков электронами. Второе неравенство (36.6) сводится к следующему:

mu2γ >> γ 5κT .	(36.15)
b
~	~

Из (36.7) следует оценка | v | ≈ Ω | z | , с учетом которой легко видеть, что неравенство (36.14)

и(36.15) эквивалентны.

Вслучае холодного электронного пучка, при Tb → 0 , функция распределения (36.13)

записывается в виде

Для окончательного решения поставленной задачи необходимо найти условие самосогласования поля (36.1) и функции распределения (36.13) (или (36.16)). Предварительно следует 2π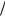kz0 - периодическую функцию разложить в тригонометрический ряд. Это удобно сделать, используя известное соотношение

n=∞	2π	n=∞	2π

∑exp(inkz0 z) =		∑δ z − n		.	(36.17)
	kz0
n=−∞		n=−∞	kz0

Рассмотрим вспомогательную функцию

s=∞	2π		2
	2π			.	(36.18)

ϕ(z) = ∑exp−α z − s	k	z0
s=−∞		z0
s=−∞

Представим каждый член ряда (36.18) в виде интеграла Фурье

175

Александров А.Ф., Кузелев М.В. Физика электронных пучков

2π

exp−α

z − s

−

+ iλz −iλs

πz ∫

exp

Тогда, с учетом (36.19), получим

s=∞

2π

(z) =

∫

+ iλz

∑

πz

exp−

exp iλs

dλ =

s=−∞

kz0

s=∞

δ(λ − sk

)dλ =

kz0

s=∞

∫

+ iλz

∑

−

2 πz

exp−

exp

s=−∞

2 πz s=−∞

(36.19)

			(36.20)
	2
s	2 kz0	+ iskz0
s	4z	+ iskz0	λ .
	4z

Теперь не представляет труда записать функцию распределения (36.13) в виде следующего тригонометрического ряда:

	m		m		2	s=∞	2 3
fb (t, z, v) = n0b		exp −		(v −u)				kz0κTb
	2πκTb		2κTb			∑exp	− s γ	cos[s(ω0t − kz0 z)]. (36.21)
						s=−∞		2eE0

Выполняя в (36.21) интегрирование по скоростям, получим выражение для плотности заряда электронного пучка

s=∞				kz
	2		3	kz	0κTb
ρb (t, z) = en0b ∑exp	− s	γ				cos[s(ω0t − kz0 z)].	(36.22)
ρb (t, z) = en0b ∑exp	− s	γ				cos[s(ω0t − kz0 z)].	(36.22)
s=−∞				2eE0

Выражение для плотности заряда (36.22), электрическое поле (36.1) и вычисленное из урав-

нений (32.3) и (32.1) выражение для плотности заряда плазмы ρp (t, z) следует подставить в

уравнение Пуассона (32.2). В результате и будет получено условие самосогласования поля (32.1) с функцией распределения электронов пучка. При этом следует учитывать, что выражение (36.22) содержит все гармоники по индексу s , а в формуле (36.1) присутствует только первая гармоника s =1. Заметим, что нулевую гармонику учитывать не нужно, поскольку она определяет постоянную составляющую плотности заряда, которая нейтрализована неподвижным ионным фоном плазмы. Поэтому при подстановке поля в уравнение Пуассона вместо (36.1) исходим из следующего его выражения:

Ez (t, z) = E0 sin(ω0t − kz0 z) + ∑Es sin[s(ω0t − kz0 z)],	(36.23)
\|s\|≥2

а впоследствии установим условие, при котором высшими гармониками в (36.23) можно пренебречь.

Результат подстановки оказывается следующим:

−3

3 kz0κTb

1 −

ωLe

+ 2

ωLbγ

−

= 0 .

(36.24)

exp

Ω

2eE0

ω0

−3

kz0κTb

ωLe

+ 2

ωLbγ

− s

= 0, | s |≥ 2 .

(36.25)

2eE

1 − s2ω

s2Ω2

exp

Равенство (36.24) следует рассматривать как условие самосогласования электрического поля

176

Александров А.Ф., Кузелев М.В. Физика электронных пучков

(36.23) и функции распределения (36.13) - нелинейное дисперсионное соотношение. А из (36.25) можно определить амплитуды высших гармоник напряженности электрического поля. Используя (36.24), перепишем (36.25) в виде

	2		2
Es = E0	ω0	−ωLe			− (s −1)	2		3	kz0κTb
				exp			γ			.	(36.26)
	2	2	2	exp			γ			.	(36.26)
	s ω0 −ωLe								2eE0
Из (36.26) следует, что \|				Es \| << \| E0 \| , т.е. высшими гармониками в (36.23) можно пренебречь
только при \| ω02 −ωLe2			\| << ωLe2 .		В частности, отбросить высшие гармоники поля можно, если

рассматриваемое нелинейное равновесное состояние замодулированного пучка в плазме возникло в результате нелинейного насыщения резонансной пучково-плазменной неустойчивости. Ранее в § 35 было независимо установлено, что высшими гармониками можно пренебречь именно при резонансной неустойчивости. При апериодической пучковой неустойчивости в плазме этого сделать нельзя (см. систему уравнений (35.24)).

В случае холодного электронного пучка из (36.24) получаем следующее нелинейное дисперсионное соотношение:

1 −	ω2	ω2	γ	−3	(36.27)
1 −	Le + 2	Lb		= 0 .	(36.27)
	ω2	Ω2
	0

Уравнения (36.24) и (36.27) описывают множество положений равновесия в системе промодулированный электронный пучок и потенциальная плазменная волна. Поле, необходимое для удержания захваченных электронов в потенциальных ямах волны, легко выражается через другие параметры системы. Например, при Tb = 0 , из уравнения (36.27) имеем

\| eϕ		\|=	eE	0	= 2	ω2	mu2 .	(36.28)
	0					Lb
			kz0			ωLe2 −ω02

Если теперь предположить, что равновесное состояние возникло в результате нелинейного насыщения резонансной пучковой неустойчивости в плазме, то создается возможность оце-

нить из (36.28) амплитуду захвата электронов пучка. Действительно, если под ω0						понимать
действительную часть частоты (32.7) и (32.11), т.е. ω	0	= ω	Le	− (1 2)ω ν1 3 , где ν -		параметр
	0		Le		Le
(32.19), то из (36.28) имеем следующую оценку:
\| eϕ0 \|= eE0 kz0 = 8ν 2 3mu2γ 3 = 27 3 (ωLb2 ωLe2 )2 3 mu2γ ≈ 5(ωLb2					ωLe2 )2 3 mu2γ .	(36.29)

Примерно к такому же значению приводит, с учетом третьей формулы (35.4), численное решение точной системы уравнений (35.5), представленное на Рис. 35.1.

Найденные равновесные состояния, как показывает их дальнейшее исследование, неустойчивы. Однако они дают возможность оценки средних значений возмущенных величин на стадии насыщения резонансных пучковых неустойчивостей в плазме.

177

Александров А.Ф., Кузелев М.В. Физика электронных пучков

§ 37. Резонансная пучковая неустойчивость в плазменном волноводе

Рассмотрим неустойчивость электронного пучка в волноводе произвольного поперечного сечения с плазменным заполнением. Используем уравнения (28.5), (28.7), дополнив их уравнением для плотности электронного тока в плазме je :

∂

∆

2 −

∂z

∂t

ψ = −4πPb (r ) jb − 4πPe (r ) je ,

∂t

∂

ω2

−3 ∂E

∂j

ω2

+ u

z ,

e =

Le E

(37.1)

∂t

∂z

4π ∂t

∂t

4π

Σ=0 = 0.

Здесь P (rr

) - профиль поперечного распределения плотности плазмы, Σ = 0 - уравнение ме-

таллической поверхности волновода, а Ez

вычисляется по последней формуле (28.6). Задача

(37.1) оказывается весьма емкой и физически содержательной. В полном объеме она рассматривается в специальном разделе физики плазмы – плазменной СВЧ-электронике (см.

§ 50). Сейчас мы ограничимся случаем однородной плазмы – P (rr

) =1 , и электронного пуч-

ка малой плотности.

В случае однородного в поперечном сечении волновода пучка, когда P (rr

) =1, поля-

ризационный потенциал имеет вид

ψ (t, z, rr

) = const ϕ

(rr

) exp(−iωt + ik

z) ,

(37.2)

где ϕ

(rr ), n =1,2,K, - собственная функция поперечного сечения волновода.

Подставляя

(37.2) в (37.1), получаем следующее дисперсионное уравнение:

ω2

ω2 γ −3

k n + kz −

1 −

−

= 0 ,

(37.3)

(ω − kzu)

где k n - поперечное волновое число волновода, соответствующее функции ϕn (rr ) .

Если положить в (37.3) ωLb = 0 , подставить kz = ωu , то можно определить частоту и волновое число, на которых имеет место черенковский резонанс плазменной волны в волноводе и свободного электрона пучка

ω0n = ωLe2 − k 2nu2γ 2 , kz0n = ω0n u .

(37.4)

Для каждой поперечной моды плазменного волновода резонансная частота (37.4) своя. Известно, что собственные значения образуют возрастающую числовую последовательность

k 21 < k 2	2 <K< k 2n <K. Поэтому для высоких поперечных мод, у которых
ωLe2 < k 2nu2γ 2 ,		(37.5)

черенковский резонанс невозможен. Если же неравенство (37.5) выполнено и для основной

178

Александров А.Ф., Кузелев М.В. Физика электронных пучков

плазменной моды с n =1, то черенковский резонанс отсутствует вообще. В случае электронного пучка малой плотности (точнее, бесконечно малой плотности) отсутствие черенковского резонанса фактически означает отсутствие пучково-плазменной неустойчивости в волноводе. Если же плотность пучка достаточно велика, то неустойчивость, конечно, возможна и при ωLe2 < k 21u2γ 2 . Будем считать, что выполнено неравенство, противоположное (37.5).

Ранее, при рассмотрении резонансной пучковой неустойчивость в безграничной плаз-

ме, решение дисперсионного уравнения (32.4) мы искали в виде ω = ωLe +δω = kzu +δω . В

случае резонансной пучково-плазменной неустойчивости в волноводе решение дисперсионного уравнения следует искать в аналогичной форме, а именно:

ω = ω0n +δω = kzu +δω, | δω | << ω0n .

(37.6)

Подставляя, с учетом (37.4), решение (37.6) в дисперсионное уравнение (37.3), преобразуем последнее к следующему виду:

δω 3			2		2	δω	ω2	γ −3
		− 2γ	2	β	2		Lb						.	(37.7)
							2	2	2 2		4
	= 1						2	2	2 2	γ	4	)
ω0n						ω0n	2(ωLe + β		k nu	γ		)

Кубическое относительно δωω0n уравнение (37.7) решается точно по формулам Кардана.

Мы же, чтобы избежать громоздких формул, приведем здесь решения только для случая электронного пучка малой плотности. При выполнении неравенства

	2γ 2 β 2		δω	<<1						(37.8)
			ω0n
из уравнения (37.8) находим следующее выражение для поправки к частоте δω :
								1 3
		−1 + i 3				2	−3
δω =		−1 + i 3			1	ωLbγ			ω0n .	(37.9)
δω =			2		2 ωLe2	+ β 2k 2nu2γ 4			ω0n .	(37.9)

Формула (37.36) определяет инкремент резонансной черенковской пучковой неустойчивости в плазменном волноводе. Эту общую формулу целесообразно проанализировать для двух противоположных предельных случаев. В случае сверхплотной плазмы (или нерелятивистского электронного пучка) когда выполнено неравенство

ωLe2	>> β 2k 2nu2γ 4 ,							(37.10)
выражение (37.9) сводится к следующему:
		−1 + i	3	2	−3	1 3
δω	=	−1 + i	3	ωLbγ			ω0n .	(37.11)
δω	=			2			ω0n .	(37.11)
		2		2ωLe

Этот инкремент отличается от инкремента (32.11) одномерного потенциального приближе-

ния только заменой ωLe на ω0n , что связано с изменением резонансной частоты. При перехо-

179

Александров А.Ф., Кузелев М.В. Физика электронных пучков

де к одномерному случаю ( k 2n → 0 ) неравенство (37.10) выполняется автоматически,

ω0n → ωLe , и выражение (37.11) переходит в (32.11).

Рассмотрим теперь противоположный предел относительно редкой плазмы или релятивистского пучка электронов, когда выполнено неравенство противоположное (37.10)

ωLe2	<< β 2k 2nu2γ 4 .	(37.12)
Поскольку	при резонансной неустойчивости должно быть	ωLe2 > k 2nu2γ 2 , то неравенство

(37.12) автоматически означает сильный релятивизм пучка, т.е. γ >>1 ( β ≈1). При этом из

(37.9) получается качественно иное выражение для инкремента

	−1 + i	3	2	−7		1 3
δω =	−1 + i	3	ωLbγ		2		ω0n .	(37.13)
δω =			2		2		ω0n .	(37.13)
	2		2k nu

Это – инкремент резонансной черенковской неустойчивости релятивистского пучка в волноводе. Возбуждаемая при такой неустойчивости плазменная волна является сильно непотенциальной, что и нашло отражение в необычной зависимости инкремента (37.13) от релятивистского фактора γ . В потенциальном приближении аналога для инкремента (37.13) нет.

Условие применимости выражения для инкремента (37.13) получается его подстановкой в неравенство (37.8), что дает

	ω2	γ	−1	1 3
4	Lb		2		<<1 .	(37.14)
4	2		2		<<1 .	(37.14)
	k nu

Из формулы (26.18) несложно показать, что если ток сплошного по сечению круглого волновода ультрарелятивистского электронного пучка равен предельному вакуумному току, то имеет место равенство

ω2	γ −1	=	π		≈1.	(37.15)
Lb
k 2	u2		µ
1				01

Поэтому, в случае ультрарелятивистского пучка резонансная неустойчивость с инкрементом (37.13) имеет место (по крайней мере для низших поперечных мод) только при условии, что ток пучка меньше предельного вакуумного тока.

Прейдем теперь к рассмотрению неустойчивости в плазменном волноводе тонкого электронного пучка с поперечным профилем Pb (rr ) = Sbδ(rr − rrb ) . В случае резонансной не-

устойчивости пучка малой плотности искажение поперечной структуры поля плазменной волны невелико. Поэтому поляризационный потенциал можно по-прежнему искать в виде (37.2), а пучок учесть по теории возмущений. Для этого подставим решение (37.2) в систему

(37.1), исключим из нее jb и je , домножим первое уравнение на ϕn (rr ) и проинтегрируем его по поперечному сечению волновода. В результате получим дисперсионное уравнение

180

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2918 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Соседние файлы в папке ЭЛТ

#
29.03.20164.53 Mб3427_VaN[1].pdf
#
29.03.2016116.12 Кб20Мониторы с ЭЛТ лекция.mht
#
29.03.20166.45 Кб22Схема монитора с ЭЛТ.gif
#
29.03.201634.05 Кб21Устройство кинескопа.jpg
#
29.03.2016133.55 Кб21Устройство монитора на ЭЛТ.jpg
#
29.03.201622.05 Кб22Устройство ЭЛТ.gif