Александров А.Ф., Кузелев М.В. Физика электронных пучков
0.8 |
δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
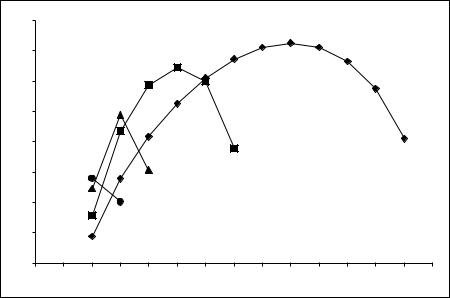
Рис. 44.1
Безразмерные инкременты диокотронной неустойчивости для различных радиусов пучка в волноводе с R = 2см:
1 - |
rb1 = 0.95 , rb2 |
=1.05см ; 2 - rb1 = 0.9 , rb2 =1.1см; |
3 |
- rb1 = 0.8 , rb2 |
=1.2см; 4 - rb1 = 0.7 , rb2 =1.3см |
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Часть III. Применение электронных пучков для получения сверхвысочастотного излучения
Глава IX. Теоретические основы высокочастотной электроники
§ 45. Основные уравнения электроники высоких частот
Одно из важных и интересных применений электронных пучков связано с решением проблемы получения мощного когерентного сверхвысокочастотного (СВЧ) электромагнитного излучения. СВЧ излучение используется для радиолокации, в системах дальней связи, для передачи энергии на большие расстояния, при осуществлении различных воздействий на вещество, в биологических исследованиях и медицинских разработках и во многих других областях. В данной главе мы изложим общую линейную теорию источников высокочастотного электромагнитного излучения на электронных пучках – СВЧ генераторов, а следующую главу посвятим конкретным СВЧ излучателям на электронных пучках и некоторым вопросам их нелинейной теории.
При изложении общей линейной теории СВЧ генераторов электромагнитного излучения исходим из следующих уравнений, описывающих в линейном приближении черенковское взаимодействие прямолинейного электронного пучка с некоторой замедляющей электродинамической системой волноводного типа (в следующей главе будут рассмотрены конкретные примеры волноводных электродинамических систем):
|
|
∂ |
|
∂ |
2 |
|
|
|
|
|
|
|
|
|
|
|
+U |
|
|
ˆ |
2 |
A |
= −ω |
2 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
b |
ˆ |
|
Lb |
b |
|
Lb b |
ˆ |
|
w |
(45.1) |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
Dw (ωˆ, kˆ)Aw = −ωw2Qw (ωˆ, kˆ) Ab .
Здесь Ab (t, z) − функция, характеризующая состояние электронного пучка – например, воз-
мущение плотности его заряда, Aw (t, z) − функция, характеризующая состояние электроди-
намической системы – например, потенциал электрического поля, Dw (ωˆ , kˆ) − дифференци-
альный оператор, описывающий динамику электродинамической системы, Gb , Qb и
Qw − некоторые безразмерные операторы, ωw − величина размерности частоты (она введена для удобства записи последующих формул), ωLb − ленгмюровская частота электронов пучка,
U - невозмущенная |
скорость пучка (ранее использовалось обозначение |
u ), а ωˆ и |
ˆ |
|
|
|
|
|
k - дифференциальные операторы частоты и продольного волнового числа: |
|
|
∂ |
|
ˆ |
|
∂ |
|
|
ωˆ = i ∂t , |
k = −i ∂z . |
(45.2) |
При написании (45.1) предполагалось, что электронный пучок движется со скоростью U вдоль электродинамической системы, ориентированной по оси OZ . Например, если безгра222
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ничный пучок движется в безграничной холодной электронной плазме, то: Gb = Qb = Qw =1 ,
ωw = ωLe , Dw (ωˆ, kˆ) = −ωˆ 2 +ωLe2 , а ωLe - ленгмюровская частота электронов плазмы (см. § 32). Уравнения (45.1) получены обобщением результатов исследования многих систем (вакуумных и плазменных), в которых реализуется вынужденное черенковское и дипольное излучение электронных пучков и вынужденное рассеяние интенсивных электромагнитных волн на пучках. Уравнениями типа (45.1) описывается и вынужденное циклотронное излучение винтовых электронных пучков во внешнем магнитном поле. Заметим еще, что если по-
ложить Qb = 0 , то первое уравнение системы (45.1) будет описывать волны плотности заряда электронного пучка – быструю и медленную, подробно рассмотренные нами в §§ 27, 28.
Если подставить в уравнения (45.1) Ab , Aw = Ab0 , Aw0 exp(−iωt + ikz) и исключить по-
стоянные Ab0 , Aw0 , то получится дисперсионное уравнение (39.2), в котором только измене-
ны обозначения: |
k |
u → kU , |
−ω2 + Ω2 |
→ D |
(ω, k) , |
Ω2 |
→ G ω2 |
, |
ΘΩ2 |
Ω2 |
→ Q Q ω2ω2 . |
|
z |
|
Le |
w |
|
Lb |
b Lb |
|
Le |
Lb |
b w w Lb |
Поэтому, проведенный в § 39 анализ дисперсионного уравнения (39.2) и данная там классификация резонансных пучковых неустойчивостей фактически без изменения переносятся на дисперсионное уравнение системы (45.1) и те резонансные процессы, которые этой системой описываются.
Резонансное взаимодействие электронного пучка с электродинамической системой возможно только при наличии решения у следующей системы (см. (39.5)):
|
(ω − kU )2 −Gb (ω, k)ωb2 = 0, |
(45.3) |
|
Dw (ω, k) = 0, |
|
|
где ω и k - частота и волновое число. Предположим, что система уравнений (45.3), опреде-
ляющая на плоскости k, ω резонансную точку, имеет решение: k = k0 , ω = ω0 . Интересуясь только резонансным взаимодействием электронного пучка и электродинамической системы, представим решение уравнений (45.1) в виде
|
|
|
A (t |
~ |
|
|
|
t +ik |
|
z), |
|
|
|
|
|
, z) = A (t, z) exp(−iω |
|
|
(45.4) |
|
|
|
b |
|
~b |
|
|
0 |
|
0 |
|
|
|
|
|
Aw (t, z) = Aw (t, z) exp(−iω0t +ik0 z). |
|
|
Здесь |
~ |
|
|
|
|
|
|
|
|
|
|
Aw (t, z) − амплитуда собственной волны электродинамической системы. Считаем, что |
выполнены неравенства |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
~ |
|
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂Aw |
|
|
∂Aw |
<< |
|
|
(45.5) |
|
|
|
∂t |
|
<< | ω0 Aw |, |
|
∂z |
| k0 Aw | , |
|
|
|
|
|
|
|
|
|
|
|
|
|
означающие медленность изменения амплитуды |
~ |
~ |
Aw (t, z) . Что касается функции |
Ab (t, z) , |
имеющей смысл амплитуды пучковой волны, то каких-либо предположений о медленности
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ее изменения пока не делается. Подставляя (45.4) в уравнения (45.1), учитывая, что в резо-
нансной точке D (ω |
, k |
0 |
) = 0 и (ω |
0 |
− k U )2 |
−G (ω |
, k |
0 |
)ω2 = 0 , и используя неравенства (45.5), |
|
|
|
w |
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
b |
|
|
0 |
|
|
b |
|
|
|
|
|
получим следующую систему уравнений для амплитуд |
~ |
|
и |
~ |
|
Ab (t, z) |
Aw (t, z) (знак «~» для крат- |
кости в дальнейшем опускаем): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
+U |
∂ |
2 |
A |
|
m |
2i G |
(ω |
, k |
|
)ω |
∂ |
+U |
∂ |
|
|
|
2 |
Q (ω |
, k |
|
) A , |
|
∂z |
|
|
|
|
|
∂z |
A |
= −ω |
|
∂t |
|
|
|
b |
|
|
b |
0 |
|
|
|
0 |
|
|
b ∂t |
|
|
|
b |
|
b b |
0 |
|
0 |
w |
∂ |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂D |
|
(ω |
, k |
|
) |
|
−1 |
|
|
|
|
|
|
|
(45.6) |
+V |
|
|
|
= −iω2Q (ω |
|
, k |
|
) |
|
|
|
A . |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
w |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
∂t |
|
g ∂z |
w |
|
|
w w |
0 |
|
|
|
0 |
|
|
|
∂ω |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
Здесь Vg = −(∂Dw |
∂k) |
(∂Dw ∂ω) − групповая скорость волны в электродинамической систе- |
ме невозмущенной электронным пучком.
Уравнения (45.6), являясь довольно общими, описывают два предельных режима вынужденного излучения электронным пучком собственных волн электродинамической системы: режим коллективного вынужденного эффекта Черенкова и режим одночастичного вынужденного эффекта Черенкова (а также и режим переходный между названными эффектами). В режиме коллективного эффекта выполнено неравенство (оно является операторным
аналогом неравенства (39.12)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
+U |
∂z Ab |
<<| |
Gb ωb Ab | , |
|
|
|
|
|
|
|
|
|
|
|
(45.7) |
и уравнения (45.6) записываются в следующем виде: |
|
∂ |
+U |
∂ |
= m |
1 |
iω |
|
Q (ω |
, k |
) |
A , |
|
|
|
|
|
A |
2 |
|
b |
0 |
|
|
|
0 |
|
) |
|
|
|
|
∂t |
|
|
∂z b |
|
|
b |
G (ω |
0 |
, k |
0 |
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
(45.8) |
∂ |
|
|
∂ |
|
|
|
|
|
|
|
|
|
∂D |
|
(ω |
, k |
) |
−1 |
+V |
|
= −iω2Q (ω |
, k |
) |
|
|
|
|
A |
|
|
|
w |
0 |
0 |
|
A . |
|
∂t |
|
g ∂z w |
|
|
w w |
0 |
0 |
|
|
|
|
|
|
∂ω |
|
|
b |
|
Верхний знак здесь берется при резонансе электродинамической волны с быстрой волной пучка, а нижний – в случае резонанса между электродинамической и медленной пучковой волнами. Коллективный эффект Черенкова есть резонансное взаимодействие электродинамической волны именно с медленной волной пучка, энергия которой отрицательна. Поэтому,
выбирая в (45.8) нижний знак (плюс) и переопределяя амплитуду Ab , запишем уравнения
(45.8) в виде
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
∂ |
|
= ia2 A |
|
|
|
+ U |
|
|
A |
, |
∂t |
|
|
|
|
|
∂z |
b |
w |
(45.9) |
∂ |
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
+ V |
|
|
|
|
A |
= −iA , |
∂t |
|
|
|
|
|
|
g ∂z |
w |
b |
|
где введено важное для дальнейшего обозначение
Александров А.Ф., Кузелев М.В. Физика электронных пучков
a2 = |
1 |
ω |
ω2 |
Q (ω |
, k |
)Q (ω |
, k |
) ∂D (ω |
, k |
) |
−1 |
(45.10) |
2 |
b |
0 |
0 |
|
w |
0 |
0 |
w |
0 |
0 |
|
> 0 . |
|
b |
w |
|
G (ω |
, k |
) |
|
|
∂ω |
|
|
|
|
|
|
|
|
|
|
b |
0 |
0 |
|
|
|
|
|
|
|
|
Параметр (45.10) содержит всю информацию о конкретной физической природе рассматри-
ваемой системы. Основной физический смысл параметра a2 состоит в том, что инкремент неустойчивости при коллективном вынужденном эффекте Черенкова равен Imω = a , в чем легко убедиться из дисперсионного уравнения системы (45.9) (подробнее см. далее).
В режиме одночастичного эффекта выполнено неравенство противоположное (45.7) (оно является операторным аналогом неравенства (39.9))
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
+U |
|
∂z Ab |
>>| |
Gb ωb Ab |, |
|
|
|
|
|
|
|
|
и уравнения (45.6) записываются в виде |
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
∂ |
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+U |
|
|
|
|
A |
= −b |
A , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
b |
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+V |
|
|
|
|
|
A |
= −iA , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
g ∂z |
w |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
3 |
|
|
2 |
2 |
Q |
|
|
, k |
)Q |
|
|
, k |
|
∂D |
w |
(ω |
, k |
) |
|
−1 |
- |
|
|
|
|
|
|
|
|
|
= ω |
|
ω |
(ω |
w |
(ω |
) |
|
|
|
|
|
|
> 0 |
|
|
|
|
b |
|
|
w |
|
b |
0 |
0 |
|
|
0 |
0 |
|
|
|
∂ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
еще один параметр, содержащий всю информацию о конкретной физической природе рассматриваемой системы. Вычисление параметров (45.10) и (45.13) для некоторых вакуумных и плазменных систем проведено в следующей главе. Инкремент неустойчивости при одно-
частичном вынужденном эффекте Черенкова равен Imω = b 3 2 , что и определяет физиче-
ский смысл параметра (45.13).
В следующих параграфах данной главы коллективный и одночастичный эффекты Черенкова рассматриваются в ограниченной области пространства 0 < z < L , моделирующей резонатор, в котором и происходит возбуждение СВЧ электромагнитных волн. Поэтому необходим учет отражения излучаемой пучком электромагнитной волны от границ z = 0 и z = L . Обозначим через Bw амплитуду электромагнитной волны, распространяющейся на-
встречу излучаемой пучком волне с амплитудой Aw . Считая, что волна Bw с электронным пучком не взаимодействует, запишем следующее очевидное уравнение для её амплитуды
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|
−V |
|
|
B |
= 0. |
(45.14) |
∂t |
|
|
|
g ∂z |
w |
|
|
Уравнения (45.9), (45.12), (45.14) должны быть дополнены условиями на амплитуды волн на границах z = 0 и z = L . Эти условия существенно зависят от знака групповой скоро-
Александров А.Ф., Кузелев М.В. Физика электронных пучков
сти Vg . Если Vg > 0 , то говорят о взаимодействии пучка с попутной волной электродинами-
ческой системы, случай Vg < 0 относится к взаимодействию со встречной волной.
При Vg > 0 |
в коллективном режиме уравнения (45.9), (45.14) дополняются следую- |
щими граничными условиями: |
|
Ab (t,0) = 0, |
Aw (t,0) = κ1Bw (t,0), Bw (t, L) =κ2 Aw (t, L). |
(45.15) |
Здесь κ1 - коэффициент отражения электромагнитной волны от границы z = 0 , а κ2 - коэффи-
циент отражения от границы z = L (| κ1,2 |≤1). Первое условие в (45.15) означает, что на гра-
ницу z = 0 электронный пучок приходит без возмущений (считаем, |
что скорость пучка |
U > 0 , т.е. пучок распространяется в положительном направлении оси Z ). |
При Vg < 0 |
граничные условия для уравнений коллективного режима (45.9), (45.14) |
имеют иной вид |
|
|
Ab (t,0) = 0, |
Bw (t,0) =κ1 Aw (t,0), Aw (t, L) = κ2 Bw (t, L). |
(45.16) |
Перейдем теперь к формулировке граничных условий для уравнений (45.12), (45.14), описывающих пучковые неустойчивости, обусловленные одночастичным эффектом Черенкова.
При Vg > 0 в одночастичном режиме уравнения (45.12), (45.14) дополняются следующими граничными условиями:
|
Ab (t,0) = 0, |
∂Ab (t,0) |
= 0, |
Aw (t,0) = κ1Bw (t,0), |
Bw (t, L) = κ2 Aw (t, L) , |
(45.17) |
|
∂z |
|
|
|
|
|
|
|
|
а если Vg < 0 граничные условия имеют иной вид: |
|
|
|
Ab (t,0) = 0, |
|
∂Ab (t,0) |
= 0, |
Bw (t,0) = κ1 Aw (t,0), |
Aw (t, L) = κ2 Bw (t, L). |
(45.18) |
|
|
∂z |
|
|
|
|
|
|
|
Сформулированные линейные краевые задачи для уравнений (45.9), (45.14) и (45.12), (45.14) являются основой, излагаемой ниже, теории СВЧ генераторов черенковского типа.
§ 46. Генераторы попутных волн на коллективном вынужденном эффекте Черенкова
Изложение теории СВЧ генераторов электромагнитных волн начнем с генерации в режиме коллективного эффекта Черенкова в случае Vg > 0 , когда излучаемая волна распро-
страняется в ту же сторону, что и пучок, т.е. рассмотрим коллективный режим возбуждения попутной волны в ограниченной области пространства. Представляя решения уравнений (45.9), (45.14) в экспоненциальной форме, ~ exp(−iωt +ikz) , получим следующие дисперси-
онные уравнения:

Александров А.Ф., Кузелев М.В. Физика электронных пучков
D (ω, k) ≡ (ω − kU )(ω − kV |
)+ a2 |
= 0, |
|
1 |
g |
|
|
(46.1) |
D2 (ω, k) ≡ (ω + kVg )= 0. |
|
|
|
|
|
|
|
Заметим, что входящие в уравнения (46.1) ω и k не являются «истинными» частотой и волновым числом: в соответствии с формулами (45.4) они определяют отклонения от резонанс-
ных значений ω0 и k0 . Заметим также, что при k = 0 из первого уравнения (46.1) следует максимальный инкремент Imω = a неустойчивости при коллективном эффекте Черенкова в безграничной системе. Ниже мы увидим, что инкремент неустойчивости, развивающейся в ограниченной области пространства, всегда меньше a , либо неустойчивости нет вообще.
Используя (46.1), запишем общее решение уравнений (45.9), (45.14) в виде (без общего множителя exp(−iωt) )
Aw (z) = Aexp(ik1 (ω)z)+ B exp(ik2 (ω)z), |
|
|
|
|
|
|
|
|
|
Ab (z) = − |
|
a2 |
|
|
Aexp(ik1 (ω)z) |
− |
|
|
a |
2 |
|
B exp(ik2 (ω)z), |
|
(46.2) |
(ω − k1U ) |
(ω − k2U ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bw (z) = C exp(ik3 (ω)z). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
(ω) = |
1 |
1 |
+ |
|
1 |
|
1 |
ω |
2 |
1 |
− |
1 |
2 |
− |
a2 |
, |
k |
(ω) = − |
ω |
- |
(46.3) |
|
|
ω |
|
|
± |
|
|
|
|
|
|
|
|
1,2 |
|
2 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
VgU |
|
3 |
|
Vg |
|
|
|
|
Vg |
|
U |
|
|
Vg |
|
|
U |
|
|
|
|
|
|
решения дисперсионных уравнений (46.1) относительно волновых чисел k . Попутно установим условие, при котором излучение пучка можно действительно считать коллективным эффектом Черенкова. Для этого подставим решение (46.2) в неравенство (45.7) и получим следующее искомое условие:
a << |
G Vg ω |
|
, |
(46.4) |
|
b U |
b |
|
|
означающее, что плотность электронного пучка должна быть достаточно велика ( a ~ |
ωb ). |
Неравенство (46.4) является аналогом неравенства (39.15).
Подставляя решения (46.2) в граничные условия (45.15) и исключая постоянные A, B
и C , получим следующее характеристическое уравнение для определения неизвестной собственной частоты ω (или набора частот), рассматриваемой системы конечной длины L :
|
ω − k1U |
ω − k2U |
|
|
exp(ik3 L) =κ1κ2 |
|
|
|
exp(ik1L) + |
|
|
|
|
exp(ik2 L) . |
(46.5) |
(k |
|
− k )U |
(k |
− k |
|
)U |
|
|
2 |
1 |
|
1 |
|
2 |
|
|
|
Поскольку в общем случае уравнение (46.5) решается только численно, рассмотрим два предельных случая. При a = 0 , т.е. когда электронного пучка нет, уравнение (46.5) сводится к следующему:

Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
|
|
ω |
|
|
|
κ κ |
exp |
2i |
|
L |
=1. |
(46.6) |
|
1 2 |
|
|
Vg |
|
|
|
|
|
|
|
|
|
Обозначая κ1κ2 =| κ1κ2 | exp(−iφ) , из (46.1) имеем
|
ω = −i |
Vg |
ln |
1 |
|
|
+φ |
Vg |
. |
(46.7) |
|
2L |
| κ κ |
2 |
| |
2L |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Мнимая часть (46.7) является обычным декрементом затухания электромагнитных колебаний открытого резонатора. Затухание обусловлено «вытеканием» электромагнитной энергии из области 0 < z < L через полупрозрачные (| κ1κ2 |<1) границы z = 0 и z = L .
Пусть теперь выполнено неравенство
|
(U −V |
)2 |
|
|
| ω |2 |
g |
|
<< a2 . |
(46.8) |
UVg |
|
|
|
|
|
Тогда разлагая функции k1,2 (ω) в окрестности нуля и подставляя их в уравнение (46.5), име-
ем:
|
|
|
L |
|
L |
−1 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
ω = |
|
|
|
+ W |
|
|
|
|
|
|
| κ1κ2 | ch( UV |
|
L) |
|
+φ |
|
(46.9) |
V |
g |
|
|
i ln |
g |
|
. |
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂k |
|
|
−1 |
|
|
2UV |
g |
|
|
|
|
|
|
|
W |
g |
= |
|
|
1,2 |
(0) |
|
= |
|
|
|
- |
|
|
|
|
|
(46.10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ω |
|
|
|
|
|
U |
+Vg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так называемая групповая скорость сноса волн при усилении. При выполнении неравенства
|
| κ1κ2 | ch( |
a |
L) >1 |
(46.11) |
|
UVg |
|
|
|
|
мнимая часть частоты (46.9) положительна, что означает неустойчивость системы. Коллективный эффект Черенкова на попутной волне является так называемой конвективной неустойчивостью, при которой любые финитные возмущения сносятся по движению пучка и в каждой фиксированной точке пространства при t → ∞ из-за сноса затухают. Наличие границ препятствует сносу возмущений и при выполнении порогового условия (46.11) приводит к их нарастанию в любой точке z на отрезке [0, L] . Неравенство (46.11) называется стартовым условием начала генерации. Если стартовое условие не выполнено, то система (электронный пучок в резонаторе) работает в режиме усиления волн. Усиление возможно только при пода-
че на вход системы z = 0 некоторого сигнала на частоте, близкой к резонансной частоте ω0 .
В режиме генерации нарастают любые, сколь угодно малые по амплитуде, флуктуационные возмущения с частотой ~ ω0 .

Александров А.Ф., Кузелев М.В. Физика электронных пучков
Из (46.9) следует предельное соотношение
Imω →a |
2 UVg |
≤ |
1 |
a , |
(46.12) |
|
|
L→∞ |
3U +Vg |
|
3 |
|
|
|
|
|
|
причем равенство в (46.12) достигается только при Vg = 3U . Неустойчивость с инкрементом
(46.12) получила название глобальной неустойчивости. Глобальный инкремент оказывается меньше максимально возможного инкремента Imω = a обычной пучковой неустойчивости в безграничном пространстве. Это казалось бы противоречит тому, что в (46.12) сделан предельный переход к системе бесконечно большой длины. На самом деле противоречия нет: при обычной неустойчивости речь идет об эволюции возмущения, равномерно заполняющего все безграничное пространство; при глобальной неустойчивости эволюционирует волновой пакет, движущийся между удаленными границами, испытывая на этих границах последовательные отражения.
Приведем еще один метод вычисления инкремента (46.9). Пусть на границе z = 0 ам-
плитуда попутной электромагнитной волны меняется по закону |
|
Aw (0, t) =ψ (t) , |
(46.13) |
где ψ(t) - произвольная функция. На границе z = L амплитуду этой волны обозначим как
Aw (L,t) . |
|
|
|
|
|
(46.14) |
Через встречную волну Bw |
и условия отражения на границах z = 0 и z = L функции (46.13) |
и (46.14) связаны уравнением обратной связи |
|
|
|
|
|
L |
|
A (0, t) = κ κ |
A L, t − |
|
. |
(46.15) |
|
w |
1 2 |
w |
|
|
|
|
|
|
|
|
Vg |
|
Несложно показать (например, используя (46.2)), что общее решение уравнений (45.9) c граничными условиями (46.13) и первым условием (45.15) имеет вид
A |
|
z |
|
a |
z) , |
(46.16) |
(z, t) =ψ t − |
|
ch( |
|
w |
|
|
|
UVg |
|
|
|
|
Wg |
|
|
где Wg - скорость (46.10). Подставляя (46.13) и (46.16) в соотношение (46.15), получим функ-
циональное уравнение
ψ |
|
L |
− |
L |
a |
L) . |
(46.17) |
(t) = κ κ ψ t − |
|
ch( |
|
|
1 2 |
Wg |
|
|
UVg |
|
|
|
|
|
Vg |
|
|
Решение последнего уравнения имеет вид (проверяется прямой подстановкой) |
|
ψ = const exp(−iω t) , |
|
|
|
(46.18) |
где ω совпадает (46.9).

Александров А.Ф., Кузелев М.В. Физика электронных пучков
§ 47. Генераторы встречных волн на коллективном вынужденном эффекте Черенкова
Перейдем теперь к рассмотрению СВЧ генератора на коллективном эффекте Черен-
кова в случае Vg < 0 , когда излучаемая волна распространяется в сторону, противоположную направлению движения пучка, т.е. рассмотрим коллективный режим возбуждения встречной волны в ограниченной области пространства. Формулы (46.1) – (46.3) справедливы и при
Vg < 0 , но их удобно переписать заменив Vg на − | Vg | . Начнем с частного случая - границы z = L абсолютно прозрачной для электромагнитного излучения. Подставляя решение (46.2) в
граничные условия (45.16) при κ2 = 0 , получим следующее характеристическое уравнение
|
exp(i(k1 − k2 )L)= |
ω − k2U |
, |
(47.1) |
|
ω − k1U |
|
|
|
|
которое целесообразно проанализировать отдельно для самого простого частного случая равных скоростей |Vg |=U . При этом (47.1) сводится к виду
exp(2ik0 L)= ω + k0U , |
k0 = 1 |
ω2 + a2 . |
(47.2) |
|
|
ω − k0U |
U |
|
|
Легко показать, что уравнение (47.2) имеет нулевые решения ω = 0 при |
|
2a |
L |
= π(2n +1), |
n = 0,1,2,.... |
|
(47.3) |
|
|
U |
|
|
|
|
Несложно также видеть, |
что других действительных решений, кроме ω = 0 , |
у уравнения |
(47.2) нет. Найдем частоту ω при условии, что равенство (47.3) при n = 0 слегка нарушено. Полагая
|
a |
= |
π |
+δ, | δ |<<1/ L , |
(47.4) |
|
|
|
U |
2L |
|
для частоты ω из уравнения (47.2) имеем |
|
ω ≈ i |
2 a( 1 +πLδ −1). |
(47.5) |
|
|
|
π |
|
Частота (47.5) чисто мнимая, причем Imω > 0 только при δ > 0 . Отсюда и из (47.4) следует пороговое условие возникновения неустойчивости, обусловленной коллективным эффектом Черенкова на встречной волне в системе конечной длины
Это и есть стартовое условие начала генерации на низшей ( n = 0 ) продольной моде резонатора. При πLδ <<1 выражение (47.5) для частоты можно представить в виде