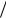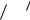Александров А.Ф., Кузелев М.В. Физика электронных пучков
|
1 |
|
|
L |
|
L 3 |
|
ψ (t) = |
|
κ1κ2ψ |
|
|
|
− |
|
|
(48.19) |
3 |
t − |
Wg |
|
∑exp(iδ jσL) . |
|
|
|
|
Vg j=1 |
|
Решение последнего уравнения имеет вид (проверяется прямой подстановкой) |
|
ψ = const exp(−iω t) , |
|
|
|
(48.20) |
где ω совпадает (48.12).
§ 49. Генераторы встречных волн на одночастичном вынужденном эффекте Черенкова
Перейдем теперь к случаю Vg < 0 , когда излучаемая волна распространяется в сторо-
ну, противоположную направлению движения пучка, т.е. рассмотрим одночастичное возбуждение встречной волны в ограниченной области пространства. Формулы (48.1), (48.2) спра-
ведливы и в этом случае, но с заменой Vg на − | Vg | , а вот простых приближенных выраже-
ний вида (48.4) не достаточно. В связи с чем теория одночастичного эффекта Черенкова на встречной волне в ограниченной области пространства оказывается весьма сложной. Поэтому здесь мы изложим не всю линейную теорию, а ограничимся только пороговым условием развития неустойчивости в системах конечной длины, т.е. определим стартовые условия начала генерации. Начнем с простого частного случая, когда граница z = L абсолютно прозрачна для электромагнитного излучения. Подставляя решение (48.2) в граничные условия
(45.18) при κ2 = 0 , получим систему линейных однородных уравнений
(ω + k1 | Vg |) A + (ω + k2 | Vg |)B + (ω + k3 | Vg |)C = 0, |
|
k1 (ω + k1 | Vg |) A + k2 (ω + k2 | Vg |)B + k3 (ω + k3 | Vg |)C = 0, |
(49.1) |
Aexp(ik1L) + B exp(ik2 L) + C exp(ik3 L) = 0. |
|
Исключая далее из (49.1) постоянные А, В и С, находим следующее характеристическое уравнение для собственных частот:
(k1 − k2 ) |
exp(ik3 L) |
|
+ (k3 − k1 ) |
exp(ik2 L) |
|
+ (k2 − k3 ) |
exp(ik1L) |
|
= 0 , |
(49.2) |
ω + k |
3 |
| V |
g |
| |
ω + k |
2 |
| V |
g |
| |
ω + k |
| V |
g |
| |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
справедливое при κ1κ2 = 0 , т.е. при нулевой (точнее минимальной) добротности резонатора,
в котором электронный пучок излучает встречную волну. Заметим, что в случае попутной волны при κ1κ2 = 0 из (48.15) при конечном L имеем Imω → −∞, что означает невозмож-
ность развития неустойчивости. Дело как известно в том, что пучковая неустойчивость на попутной волне является конвективной. Для возможности такой неустойчивости в ограниченной системе необходимо конечное отражение от ее продольных границ. Неустойчивость пучка на встречной волне является абсолютной. Такая неустойчивость возможна и при пол-

Александров А.Ф., Кузелев М.В. Физика электронных пучков
ном отсутствии отражения. С аналогичной ситуацией мы уже встречались ранее, рассматривая генерацию на попутной волне (формула (46.9)) и генерацию на встречной волне (§ 47) в режиме коллективного эффекта Черенкова.
Для учета отражения электромагнитных волн от границ z = 0, L подставим решение
(48.2) в общие граничные условия (45.18). В результате получим систему
|
(ω + k1 | Vg |) A + (ω + k2 | Vg |)B + (ω + k3 | Vg |)C = 0, |
|
|
k1 (ω + k1 | Vg |) A + k2 (ω + k2 | Vg |)B + k3 (ω + k3 | Vg |)C = 0, |
(49.3) |
|
D = κ1 ( A + B + C), |
|
|
|
Aexp(ik1L) + B exp(ik2 L) + C exp(ik3 L) = κ2 D exp(ik4 L). |
|
|
Исключая далее постоянную D , преобразуем систему (49.3) к виду |
|
|
(ω + k1 | Vg |) A + (ω + k2 | Vg |)B + (ω + k3 | Vg |)C = 0, |
|
|
k1 (ω + k1 | Vg |) A + k2 (ω + k2 | Vg |)B + k3 (ω + k3 | Vg |)C = 0, |
(49.4) |
|
A(exp(ik14 L) −κ1κ2 )+ B(exp(ik24 L) −κ1κ2 )+ C(exp(ik34 L) −κ1κ2 )= 0, |
|
где k j 4 = k j − k4 . Сравнивая теперь (49.4) с (49.1) и используя уравнение (49.2), сразу полу-
чим следующее дисперсионное уравнение, описывающее одночастичный эффект Черенкова на встречной волне с учетом конечного отражения электромагнитных волн от продольных границ резонатора:
(k |
− k |
2 |
) |
exp(ik34 L) −κ1κ2 |
+ (k |
3 |
− k |
) |
exp(ik24 L) −κ1κ2 |
+ (k |
2 |
− k |
3 |
) |
exp(ik14 L) −κ1κ2 |
= 0 . |
(49.5) |
|
|
|
1 |
|
|
ω + k3 |
| Vg | |
|
1 |
|
ω + k2 | Vg | |
|
|
|
ω + k1 |
| Vg | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения (49.2) и (49.5) удается решить только численно, но здесь мы не будем рассматривать детали этого весьма сложного численного анализа. Сформулируем только основной результат: для развития неустойчивости, обусловленной одночастичным вынужденным эффектом Черенкова на основной продольной моде ( n = 0 ) встречной волны в системе конечной длины, требуется выполнение стартового условия
3 |
U 2 | Vg | |
p(κ) |
(49.6) |
b > |
L |
|
|
|
где p(κ) - величина, близкая к двум в широком диапазоне изменения общего коэффициента отражения κ . В частности имеет место точное равенство p(0) = 2 . Неравенство (49.6) целе-
сообразно сопоставить со стартовым условием (47.27) начала генерации встречной волны при коллективном эффекте Черенкова.
Для применения полученных в Главе IX общих стартовых условий начала генерации к конкретным физическим системам требуется определить для этих систем параметры (45.10) и (45.13), что и будет сделано в заключительной главе нашего курса.
Александров А.Ф., Кузелев М.В. Физика электронных пучков
Глава IX. СВЧ приборы на релятивистских электронных пучках
§ 50. Плазменные СВЧ генераторы
Разработке плазменных источников СВЧ излучения посвящен специальный раздел физики плазмы и электронных пучков – плазменная релятивистская СВЧ электроника. В плазме имеется чрезвычайно богатый набор разнообразных электромагнитных волн, которые легко и эффективно могут возбуждаться электронным пучком, а затем - трансформироваться в вакуумную электромагнитную волну, т.е. излучаться. Для получения основных уравнений линейной плазменной СВЧ электроники исходим из системы уравнений (37.1), которую,
введя новую функцию A(t, z, rr ) = ∂ψ 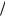 ∂t , запишем следующим образом:
∂t , запишем следующим образом:
|
|
|
|
|
|
∂ |
2 |
|
|
|
|
1 |
|
|
∂ |
2 |
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
2 |
|
− |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∆ |
∂z |
|
c |
|
|
∂t |
|
A = −4πPb (r ) jb − 4πPe (r ) je , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
2 |
je |
|
|
|
|
|
2 |
|
|
|
∂ |
2 |
|
|
|
|
|
1 |
|
∂ |
2 |
|
|
|
|
|
|
|
|
ωLe |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t2 |
= |
|
|
|
|
|
|
|
− |
|
|
|
|
A, |
|
|
(50.1) |
|
4π |
|
∂z2 |
c2 |
∂t2 |
|
|
∂ |
|
|
|
∂ 2 |
|
|
|
|
|
|
ωLb2 γ |
−3 |
|
∂2 1 |
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t + u ∂z |
|
|
jb = |
|
|
|
|
|
|
|
∂z2 − c2 ∂t2 |
|
|
|
|
|
4π |
|
|
|
A. |
Рассмотрим случай тонких (игольчатых) в поперечном сечении волновода плазмы и пучка, профили плотности которых даются формулами
|
P |
(rr |
) = S |
δ(rr |
− rr ), |
|
|
|
e |
|
|
e |
|
|
e |
(50.2) |
|
P (rr |
) = S |
δ(rr |
− rr ). |
|
|
|
|
b |
|
|
b |
|
|
b |
|
|
Здесь S |
e |
, S |
b |
и rr |
, rr |
- площади поперечных сечений и поперечные координаты плазмы и пуч- |
|
|
|
|
e |
|
b |
|
|
|
ка соответственно. Используя операторы частоты и волнового числа (45.2) и осуществляя замены 4πje → je , 4πjb → jb , преобразуем систему (50.1) к компактной форме
|
|
(∆ − χˆ 2 )A = −Pb (rr ) jb − Pe (rr ) je , |
|
|
|
ω2 |
j |
e |
= ω2 |
χ2 A, |
|
|
|
|
|
(50.3) |
|
|
ˆ |
|
|
Le ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
= ω |
2 |
γ |
−3 |
χ |
2 |
A, |
|
|
|
(ω −uk ) |
j |
b |
Lb |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
где χˆ |
2 |
|
ˆ2 |
− c |
−2 |
|
2 |
. Заметим, что во второе и третье уравнения системы (50.3) входит функ- |
|
= k |
|
ωˆ |
|
ция A(t, z, rr ) только в точках нахождения плазмы и пучка соответственно, т.е. |
A(t, z, rr ) и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
A(t, z, rr ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложим функцию A(t, z, rr ) по собственным функциям поперечного сечения волно- |
вода (см. (26.8) и (26.9)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
A(t, z, rr ) = ∑An (t, z)ϕn (rr ) . |
(50.4) |
n=1
Подставим разложение (50.4) в первое уравнение системы (50.3) и, используя ортогональ-
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ность собственных функций ϕn (rr ) , выразим коэффициенты разложения An (t, z)
|
|
|
− |
r |
|
|
r |
|
|
|
|
|
A |
(t, z) = (k 2 |
+ χˆ |
2 )1 |
|
Sbϕn (rb ) |
j |
(t, z) + |
Seϕe (re ) |
j |
(t, z) |
|
. |
(50.5) |
|
|
n |
n |
|
|
|| ϕn || |
2 |
b |
|
|| ϕn || |
2 |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь (k 2n + χˆ 2 )−1 - оператор обратный оператору k 2n + χˆ 2 . Подставим далее (50.5) в разло-
жение (50.4), а разложение (50.4) подставим во второе и третье уравнения системы (50.3). В
результате получим следующие уравнения для функций |
je (t, z) |
и |
jb (t, z) : |
|
|
|
|
|
|
|
|
|
ˆ |
2 |
2 |
|
|
−3 |
∞ |
|
2 |
|
2 |
|
|
|
|
|
2 |
|
− |
|
|
|
|
|
|
2 |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Sbϕn (rb ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−(ωˆ −uk) +ωLbγ |
|
∑ χˆ |
|
(k n + |
χˆ |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
jb = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| ϕn || |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
2 |
|
|
|
−1 |
|
S ϕ(rr)ϕ(rr ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −ωLb2 γ −3 ∑ |
χˆ |
(k 2n |
+ |
χˆ 2 ) |
|
e |
e |
|
b |
|
je , |
(50.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| ϕn || |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
2 |
|
|
|
|
|
|
|
|
−1 |
|
S ϕ |
2 |
(rr) |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
2 |
|
|
|
−1 |
|
S ϕ(rr )ϕ(rr) |
|
− |
ωˆ 2 +ωLe2 ∑ |
χˆ |
|
(k 2n + χˆ |
2 ) |
|
|
e n |
|
|
|
e |
|
|
|
je |
|
= −ωLe2 ∑ |
|
χˆ |
(k 2n |
+ |
χˆ 2 ) |
|
b |
b |
|
e |
jb . |
|
|
|
|
|
|| ϕn || |
2 |
|
|
|
|
|| ϕn || |
2 |
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что уравнения (50.6) совпадают с общими уравнениями (45.1), причем |
U = u , A |
= j |
b |
, |
A = j |
e |
, ω2 |
= ω2 |
|
, под ω |
2 |
|
|
|
в (45.1) следует понимать ω2 |
γ −3 , а операторы оп- |
b |
|
|
|
w |
|
|
|
|
w |
|
|
|
Le |
|
|
|
|
|
|
|
|
Lb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lb |
|
|
|
|
|
|
ределяются формулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
2 |
|
|
2 |
∞ |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
− |
|
|
|
2 |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Seϕn |
(re ) |
|
|
|
|
|
|
|
|
|
|
Dw (ωˆ, k) ≡ De |
(ωˆ, k) |
= −ωˆ |
|
+ωLe |
∑ χˆ |
|
|
|
(k n + χˆ |
|
) |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| ϕn || |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
ˆ |
|
|
|
|
|
|
ˆ |
= S |
Q |
|
|
|
ˆ |
|
|
|
Q |
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(ω, k) ≡ Q (ω, k) |
(ω, k), |
|
|
|
(ω, k) = S Q (ω, k), |
|
|
|
|
|
|
|
|
|
|
|
w |
ˆ |
|
|
|
e |
ˆ |
|
|
|
|
b |
|
|
0 |
|
ˆ |
|
|
|
|
|
|
|
|
|
b |
|
|
|
ˆ |
|
|
|
|
|
|
e |
|
0 |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
2 |
|
2 |
|
|
|
2 |
|
− |
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(50.7) |
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
1 |
|
ϕ(rb )ϕ(re ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q0 (ωˆ, k) |
= |
∑ |
χˆ |
|
(k n |
+ χˆ |
|
) |
|
|
|| ϕn || |
2 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
∞ |
|
|
2 |
|
2 |
|
|
|
2 |
|
− |
|
|
|
2 |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Sbϕn |
|
(rb ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gb (ωˆ, k) |
= |
∑ |
χˆ |
|
(k n |
+ χˆ |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| ϕn |
|
|
|| |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система уравнений (45.3), определяющая на плоскости |
k, ω |
резонансную |
точкуk = k0 , |
ω = ω0 , для рассматриваемого плазменно-пучкового волновода имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
χ |
2 |
|
|
|
|
|
|
2 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Db (ω, k) ≡ −(ω − ku)2 +ωbe2 γ −3 ∑ |
|
|
|
|
|
|
|
|
|
|
|
Sbϕn |
(rb ) |
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
k n |
|
+ χ |
|
|
|
|| ϕn || |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(50.8) |
|
|
|
|
|
|
|
|
|
|
|
∞ |
χ |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
De (ω, k) ≡ −ω2 +ωLe2 ∑ |
|
|
|
|
|
Seϕn |
(re ) |
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 k n + χ |
|
|
|
|
|| ϕn || |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где χ2 = k 2 −ω2 |
c2 . Приведем еще дисперсионное уравнение (39.2), являющееся следствием |
дифференциальных уравнений (50.6), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ω2 − Ω2Le ) ((ω − ku)2 − Ω2Lb )= ΘΩ2LeΩ2Lb . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(50.9) |
Здесь
Александров А.Ф., Кузелев М.В. Физика электронных пучков
∞ |
|
χ |
2 |
|
2 |
r |
|
|
∞ |
|
χ |
2 |
|
2 |
r |
|
|
Ω2Le = ωLe2 ∑ |
|
|
|
Seϕn |
(re ) |
|
, |
Ω2Lb = ωbe2 γ −3 ∑ |
|
|
|
Sbϕn |
(rb ) |
|
- |
2 |
|
2 |
|
2 |
2 |
|
2 |
|
2 |
n=1 |
k n + χ |
|
|
|| ϕn || |
|
|
n=1 |
k n + χ |
|
|
|| ϕn || |
|
|
квадраты частот собственных волн плазмы и пучка, а
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
1 |
|
|
|
ϕ |
r |
r |
2 |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
(rb )ϕ(re ) |
|
|
|
|
|
|
|
|
|
|
2 |
+ χ |
2 |
|
2 |
|
|
|
|
|
Θ = |
|
|
|
n=1 |
k n |
|
|
|
|| ϕn || |
|
|
|
|
|
|
- |
∞ |
|
|
1 |
|
|
2 |
r |
|
∞ |
|
1 |
|
|
|
2 |
r |
|
|
|
∑ |
|
|
|
ϕn |
(rb |
2) |
∑ |
|
|
|
|
ϕn |
(re |
2) |
|
2 |
|
|
2 |
2 |
+ χ |
2 |
|
n=1 |
k n + χ |
|
|
|| ϕn || |
|
n=1 k n |
|
|| ϕn || |
|
|
коэффициент связи плазменных и пучковых волн. Можно показать (см. неравенство Коши-
Буняковского), что 0 < Θ ≤1, причем равенство Θ единице имеет место только при rrb = rre .
Общие формулы (50.10) и (50.11) применимы к важной для практических применений геометрии – тонким трубчатым плазме и пучку (радиусы re и rb , толщины ∆e и ∆b ) в волно-
воде кругового сечения с радиусом R . В этом случае k n = µl,n 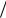 R , ϕn = Jl (k n r) , µl,n - корень функции Бесселя Jl (x) (см. пояснения к краевой задаче (26.8) и Рис. 26.1), l = 0,1,2... - азиму-
R , ϕn = Jl (k n r) , µl,n - корень функции Бесселя Jl (x) (см. пояснения к краевой задаче (26.8) и Рис. 26.1), l = 0,1,2... - азиму-
тальное волновое число. Вычисление величин (50.10) и (50.11) для цилиндрической геометрии дает следующий результат (при этом используются формулы вида (26.14)):
|
Ω2 |
= ω2 |
χ2r ∆ |
|
I 2 (χr ) |
Kl (χre ) |
− |
|
Kl (χR) |
|
, |
|
|
|
|
|
|
|
|
|
Le |
Le |
e |
e |
l |
e |
I |
(χr |
) |
|
|
I |
(χR) |
|
|
|
|
|
|
|
|
|
|
l |
|
e |
|
|
|
|
l |
|
|
|
|
|
|
(50.12) |
|
|
|
|
|
|
I 2 (χr ) |
Kl |
(χrb ) |
|
|
Kl (χR) |
|
|
Ω2 |
= ω2 |
γ −3 χ2r ∆ |
− |
, |
|
|
|
|
|
Lb |
Lb |
|
|
b b |
l |
b |
|
I |
(χr |
) |
|
|
I |
(χR) |
|
|
|
|
|
|
|
|
|
|
l |
|
|
b |
|
|
|
|
l |
|
|
|
|
|
|
Il (χrb ) |
|
Kl (χre )Il (χR)− Kl (χR)Il (χre ) |
, |
r |
≤ r |
|
|
|
|
|
(χre ) Kl |
(χrb |
)Il |
(χR)− Kl |
(χR)Il |
(χrb ) |
|
b |
e |
|
Il |
|
|
, |
(50.13) |
Θ = I |
(χr ) K |
(χr |
)I |
(χR)− K |
(χR)I |
(χr ) |
, |
rb |
I |
(χr |
) K |
(χr )I |
(χR)− K |
(χR)I |
(χr ) |
≥ re |
|
|
l |
e |
|
|
l |
b |
l |
l |
l |
b |
|
|
|
|
|
l |
b |
|
|
l |
e |
l |
l |
l |
e |
|
|
|
|
где Il (x) и Kl (x) - функции Инфельда и Макдональда соответственно.
Рассмотрим для цилиндрической геометрии систему уравнений (50.8). Второе урав-
нение этой системы ω2 = Ω2Le (ω, k) определяет собственные частоты волн плазменного вол-
новода. Среди множества таких волн имеются замедленные (| ω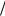 k | < c ) поверхностные вол-
k | < c ) поверхностные вол-
ны (одна для каждого l ), которые и представляют здесь для нас интерес, поскольку только они могут возбуждаться прямолинейным электронным пучком. В длинноволновом пределе,
когда k → 0 , используя асимптотики функций Il (x) |
и Kl (x) , для частот замедленных волн |
находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = kc |
ω |
Le |
, |
|
[r |
∆ |
|
ln(R r )]−1, |
|
|
l = 0, |
, |
(50.14) |
|
k 2e = |
e |
|
e |
|
|
e |
−1 |
, |
l =1,2,... |
k 2 |
c2 +ω2 |
|
2l{r |
∆ |
e |
[1 − (r R)2l ]} |
|
|
e |
|
Le |
|
|
|
|
e |
|
e |
|
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков
где, k e - поперечное волновое число замедленной поверхностной плазменной волны (в на-
ших обозначениях k ≡ kz - продольное волновое число). При большой плотности плазмы,
ωLe2 > k 2ec2 , волны (50.14) являются сильно непотенциальными. В области более коротких длин волн, порядка радиуса плазменной трубки re , частоты поверхностных волн не зависят от l и определяются выражением (как у волн на глубокой воде):
ω = ωLe (k∆e 2 )1 2 . |
(50.15) |
И наконец, при длинах волн меньших ∆e модель плазмы с профилем (50.2) просто не верна,
поскольку не учитывает запирания поля волн в объеме плазмы. Учёт конечности толщины плазмы приводит как и положено к тому, что при k 2 → ∞, ω2 →ωLe2 . Но это происходит уже когда плазменные волны сильно потенциальны и их черенковское возбуждение электронным пучком не представляет интереса для плазменной релятивистской СВЧ электроники.
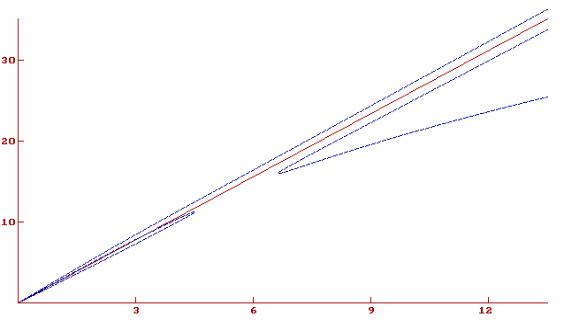
На Рис. 50.1 изображена дисперсионная кривая ω(k) симметричной ( l = 0 ) поверхно-
стной плазменной волны (кривая 1). Дисперсионная кривая построена путем численного решения второго уравнения (50.8) для следующих конкретных параметров волновода и плазмы: R =1.8см, re =1см, ∆e = 0.1см, ωLe = 35 1010 рад/ с. Начальный, почти прямолинейный,
участок дисперсионной кривой описывается формулами (50.14). На этом участке волну называют плазменной кабельной. Следующий участок кривой описывается законом дисперсии (50.15). При приближении к плазменной частоте кривая перестаёт быть верной; необходим учёт конечности толщины плазмы.
На Рис. 50.1 проведена так же прямая одночастичного черенковского резонанса
ω = ku (для скорости пучка u = 2.6 1010 cм/ c.) и обозначена точка одночастичного черенковского резонанса I – точка пересечения прямой ω = ku с дисперсионной кривой ω(k) . Не трудно видеть, что с уменьшением ωLe частота черенковского резонанса уменьшается и при
ωLe2 =ωLe2 пор. = k2eu2γ 2 (50.16)
обращается в нуль. Порог (50.16) зависит от азимутального волнового числа l , минимальный порог имеет симметричная поверхностная волна с l = 0 . Если плазменная частота меньше пороговой, то одночастичный черенковский резонанс невозможен.
Частоты пучковых поверхностных волн определяются из первого дисперсионного уравнения (50.8) (ω − ku)2 = Ω2Lb (ω, k) . На Рис. 50.1, кроме плазменных, изображены и дис-
персионные кривые симметричных ( l = 0 ) волн бесконечно тонкого трубчатого пучка при
rb = 0.65см, ∆b = 0.1см, токе пучка Ib = 2kA и γ = 2 ( u = 2.6 1010 см/ c ). Волна с большей чем u фазовой скоростью (ей соответствует кривая 3) является быстрой пучковой волной, а вол246
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ω (1010 рад с)
с)
k (см-1 )
Рис. 50.1
Спектры колебаний волновода с замагниченными тонкими плазмой и пучком (взаимодействие плазмы и пучка не учтено): 1- волна плазмы; 2- медленная волна пучка; 3- быстрая волна пучка; I - точка одночастичного черенковского резонанса;
II - точка коллективного черенковского резонанса.
Александров А.Ф., Кузелев М.В. Физика электронных пучков
на с меньшей фазовой скоростью (кривая 2) – медленной волной. Медленная волна пучка, как было уже установлено нами ранее (см. §§ 27, 28), имеет отрицательную энергию, что и приводит к неустойчивости пучка в плазме. Точка пересечения дисперсионной кривой плазменной кабельной волны 1 и дисперсионной кривой медленной пучковой волны 2 является точкой коллективного черенковского резонанса. На Рис. 50.1 она отмечена как точка II.
Именно эта резонансная точка k = k0 , ω = ω0 и определяется из системы уравнений (50.8).
Дисперсионные кривые на Рис. 50.1 такие, как если бы взаимодействие пучка и плазмы в волноводе полностью отсутствовало, т.е. параметр связи Θ в уравнении (50.9) равнялся нулю. При Θ ≠ 0 возникает неустойчивость и дисперсионные кривые качественно изменяются. На Рис. 50.2 представлены дисперсионные кривые для случая Θ =1 , когда взаимодействие пучка и плазмы сильное. Кривые получены численным решением уравнения (50.9) для следующих параметров системы: rb = re = 0.65см, ∆b = ∆e = 0.1см, γ = 2, R =1.8см, Ib = 2kA ,
ωLe = 35 1010 рад/ c . Параметры выбраны так, что выполнено неравенство ΩLb < ΘΩLe . Зна-
чит согласно (39.11) неустойчивость, к которой относится Рис. 50.2, развивается в режиме одночастичного эффекта Черенкова. Полезно сравнить Рис. 50.2 с Рис. 32.1 - разница фактически лишь в законе дисперсии плазменной волны: в случае Рис. 50.2 дисперсия определяет-
ся формулами (50.14) и (50.13), а в случае Рис. 32.1 ω = ωLe .
На Рис. 50.3 представлены дисперсионные кривые для случая Θ = 0.6 , когда взаимодействие пучка и плазмы более слабое (параметры системы взяты прежние, только радиус плазмы увеличен до re=1.1см). Видно, что область волновых чисел, где имеется неустойчи-
вость, по сравнению с предыдущим случаем сузилась, что свидетельствует об изменении ме-
ханизма неустойчивости. С уменьшением Θ начинает выполняться неравенство ΘΩLe < ΩLb
(см. (39.15)), и неустойчивость переходит в режим коллективного эффекта Черенкова. Различия между Рис. 50.3 и Рис. 39.1 обусловлены различным законом дисперсии плазменных и пучковых волн в волноводе и в безграничном пространстве.
Предположим, что плотность электронного пучка мала, т.е. выполнено сильное нера-
венство (39.7). Считаем также, что ω0 ≈ k0u << ωLe , где ω0 и k0 - резонансные частота и вол-
новое число, найденные из системы (50.8). В этих условиях, используя асимптотики функций
Il (x) и Kl (x) , дисперсионное уравнение (50.9) можно преобразовать к виду
|
2 |
|
2 |
|
ω2 |
ω2 |
|
|
2 |
|
2 |
|
2 |
ω |
2 γ −3 |
|
2 |
|
|
2 |
|
ω2 |
ω2 |
ω2 γ −3 |
|
|
|
|
|
|
Le |
|
|
|
|
|
Lb |
|
|
|
|
|
2 |
|
|
|
|
Le |
Lb |
|
|
|
|
ω |
|
− k |
|
− |
|
2 |
|
2 |
|
(ω − ku) |
|
− k |
|
u |
|
|
|
|
|
|
= Θk |
|
u |
k |
|
− |
|
2 |
|
2 |
|
|
|
|
. (50.17) |
|
|
c |
|
|
|
2 |
|
2 |
γ |
2 |
|
|
c |
2 |
2 |
γ |
2 |
|
|
|
|
|
|
|
k e |
|
|
|
|
|
|
|
k bu |
|
|
|
|
|
|
|
|
|
k e |
k bu |
|
|
|
Здесь k e - поперечное волновое число, определенное в (50.14), k b |
получается заменой в k e |
индекса "e" на индекс "b", а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ω (1010 рад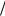 с)
с)
k (см-1 )
Рис. 50.2
Дисперсионные кривые при сильном взаимодействии плазмы и пучка ( Θ =1)
Александров А.Ф., Кузелев М.В. Физика электронных пучков
ω (1010 рад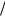 с)
с)
k (см-1 )
Рис. 50.3
Дисперсионные кривые при слабом взаимодействии плазмы и пучка ( Θ = 0.6 )