
Fiber_Optics_Physics_Technology
.pdf
A.4. Beer’s Attenuation and dB Units |
261 |
Example
Consider an amplifier that boosts some input signal from 1 to 20 mV; source and load impedance are equal. When specifying the gain factor, one needs to make the distinction between voltage gain and power gain: Gamplitude = 20, Gpower = 400. Using decibels the gain factor is simply
20mV
δ= 20 log10 1 mV = 26 dB
or
δ = 10 log |
|
400 mV2/R |
||
10 |
|
|
= 26 dB. |
|
1 mV2 |
|
|||
|
/R |
|||
Two di erent numerical values are replaced with a single value in dB. On first encounter, students tend to find this irritating, but in practical usage it is a real simplification. Of course we had to assume equal impedances at input and output, but in radio engineering that is very frequently true.
Electrical and Optical dB Units
The second source of confusion occurs when light is converted to an electric signal. As described in Sect. 8.10, common photodetectors such as, e.g., photo diodes, convert the impinging light power to a proportional electric current. The electric power delivered by the detector is thus proportional to the square of the received optical power. One therefore needs to specify whether one speaks of optical or electric dB. Consider a statement about the dynamic range of some detector, i.e., the ratio of maximum received power before severe distortion sets on and the smallest detectable power that is not masked by noise. One “dBopt” corresponds to two “dBelect.”
A.4 Beer’s Attenuation and dB Units
When light is impinging on a more or less transparent material, the reduction of power P (L) with increasing penetration depth L is described by the well-known Beer’s law:
P (L) = P0 exp (−αL) .
Here, α is called Beer’s absorption coe cient; its reciprocal value is that particular penetration depth where the initial power P0 has decayed to the fraction 1/e ≈ 37%.
By taking the logarithm, one immediately sees that
1 |
log10 |
P |
||
αL = − |
|
|
. |
|
log10 e |
P0 |
|||
On the other hand, using the definition of the dB we can write
P αdBL = 10 log10 P0 .
Comparing terms yields the conversion formula
αdB = −α10 log10 e ≈ −4.34α.
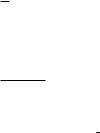
Appendix B
Skin E ect
When alternating current flows through a conductor, the current density is not necessarily constant across its entire cross-section. When J (0) denotes the current density at the surface, the current density at some depth x below the
surface is given by
J (x) = J (0)e−x/δ e−ix/δ .
Here, δ is a characteristic penetration depth, i.e., that depth where the current density is reduced by a factor of 1/e ≈ 37 % in comparison to the surface. At the same time, at this depth there is a phase shift of 1 rad. This depth is given by
δ = |
|
2ρ |
. |
(B.1) |
|
|
|
|
|||
|
ωμ0μr |
|
|||
Here, in turn, μ0 = 4π 10−7 Vs/Am is the vacuum permeability, μr the relative permeability of the material, ρ the specific resistance of the material, and ω the current’s angular frequency.
It is straightforward to realize that at a depth of πδ, there is a phase shift of 180◦. This implies that at this depth the current flows in opposite phase to that at the surface. This is, of course, a hindrance for the current flow through the conductor and is felt as an e ective increase of resistance. Somewhat paradoxically, a massive conductor, such as a solid wire, conducts current less well than a hollow conductor (a tube) of the same outside diameter!
The e ective resistance is given by
R = l |
ρ |
(B.2) |
|
δs |
|||
|
|
with l the length and s the circumference of the conductor. This should be compared with the usual expression for direct current resistance,
R = l Aρ ,
where A is the conductor’s cross-sectional area. In e ect, only a surface layer of thickness ρ contributes to the current flow.
Inserting Eq. (B.1) into Eq. (B.2) yields
R(ω) = |
l |
|
ωρμ0μr |
. |
|
s |
2 |
|
|||
|
|
|
|||
F. Mitschke, Fiber Optics, DOI 10.1007/978-3-642-03703-0 14, |
263 |
||||
c |
|
|
|
||
Springer-Verlag Berlin Heidelberg 2009 |
|
||||
264 |
Appendix B. Skin E ect |
For our consideration the relevant feature is the relation
√
R(ω) ω.
The e ective resistance grows with increasing frequency (Fig. B.1). This limits the usefulness of electrical conductors at very high frequencies. Optical fibers do not su er from a comparable limitation.
Figure B.1: Skin e ect causes the e ective resistance of a cable to rise with increasing frequency. Optical fiber is superior, in particular at high frequencies.

Appendix C
Bessel Functions
Bessel’s di erential equation reads
x2 d2y + x dy + (x2 − m2)y = 0. dx2 dx
We are only interested in solutions for integer m. They are denoted as Jm, Nm, and Hm1,2.
The modified Bessel’s di erential equation reads
x2 d2y + x dy − (x2 + m2)y = 0. dx2 dx
Solutions for integer m are denoted by Im and Km.
C.1 Terminology for the Various Functions
|
Jm |
Bessel function |
Cylinder function 1. kind |
|
|
|
1. kind |
|
|
|
|
|
|
|
Bessel’s |
Nm, Ym |
Bessel function |
Cylinder function 2. kind |
|
equation |
|
2. kind |
Weber’s function |
|
|
|
|
Neumann function |
|
|
|
|
|
|
|
H1,2 |
Bessel function |
Cylinder function 3. kind |
|
|
m |
3. kind |
Hankel function |
|
|
|
|||
|
|
|
|
|
Modified |
Im |
Modified Bessel |
|
|
Bessel’s |
|
function 1. kind |
|
|
equation |
|
|
|
|
Km |
Modified Bessel |
Modified Hankel function |
||
|
||||
|
|
function 2. kind |
McDonald’s function |
|
|
|
|
|
F. Mitschke, Fiber Optics, DOI 10.1007/978-3-642-03703-0 15, |
265 |
c Springer-Verlag Berlin Heidelberg 2009

266 |
|
|
Appendix C. Bessel Functions |
||
C.2 Relations Between These Functions |
|||||
Nm(x) = |
lim |
Jk (x) cos(kπ) − J−k (x) |
, |
||
|
k→m |
|
sin(kπ) |
|
|
Hm1,2(x) = Jm(x) ± iNm(x), |
|
||||
Im(x) = i−mJm(ix), |
|
||||
Km(x) = |
lim |
π |
I−k (x) − Ik (x) |
. |
|
|
|
||||
|
k→m |
2 sin(kπ) |
|
||
C.3 Recursion Formulae
With Zm denoting some cylinder function of type Jm, Nm, Hm, Im, or Km and with Zm(x) the derivative of Zm(x) with respect to the argument x,
xZ |
(x) |
= |
|
mZ |
m |
(x) |
− |
xZ |
(x), |
m |
|
|
|
|
|
m+1 |
|
||
xZ |
(x) |
= |
− |
mZ |
m |
(x) + xZ |
(x). |
||
m |
|
|
|
|
|
m−1 |
|
||
C.4 Properties of Jm and Km
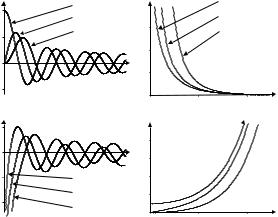
The functions Jm describe standing waves. J0 “looks like” cosine, J1 like sine. Asymptotically (for very large x) the following approximations hold:
J0(x) = |
|
2 |
|
cos(x − π/4), |
|
|
|
|
|
|
|||
|
|
πx |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J1(x) = |
|
|
2 |
|
sin(x − π/4), |
|
|
|
|
|
|
||
|
|
πx |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
Jm(x) = |
|
|
2 |
|
cos x |
− |
π/4 |
− |
nπ/2 + |
O |
. |
||
|
πx |
|
|||||||||||
|
|
|
|
|
|
x |
|
||||||
Functions with negative index are defined as
J−n(x) = (−1)n Jn(x).
There is a relation with angular functions of the form
|
+∞ |
cos(α + β sin γ) = |
Jn(β) cos(α + nγ), |
|
n=−∞ |
which is relevant in context with frequency modulation (see Sect. 11.1.2). Functions Km describe decaying cylinder waves and “look like” decaying
exponential functions. Asymptotically (for very large x), for all m the following approximations hold:
Km(x) = |
|
|
π |
|
e−x 1 + |
|
1 |
. |
|
2x |
|
||||||
|
|
|
|
O |
x |
|||
As long as the argument is larger than 2, the error is less than 5%.
C.5. Zeroes of J0, J1, and J2 |
267 |
C.5 Zeroes of J0, J1, and J2
J0 |
J1 |
J2 |
2,4048 |
0,0000 |
0,0000 |
5,5201 |
3,8317 |
5,1356 |
8,6537 |
7,0156 |
8,4172 |
11,7915 |
10,1735 |
11,6198 |
14,9309 |
13,3237 |
14,7960 |
. . . |
. . . |
. . . |
C.6 Graphs of the Most Frequently Used
Functions
1,0 |
|
J0 |
|
|
|
K0 |
|
J1 |
|
|
|
K1 |
|
|
|
|
1,5 |
|
||
|
|
J2 |
|
|
K2 |
|
0,5 |
|
|
|
|
||
|
|
|
|
1,0 |
|
|
0 |
10 |
|
|
|
|
|
5 |
|
15 |
0,5 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
-0,5 |
|
|
|
0 |
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
0 |
0.5 |
|
|
|
|
|
|
8 |
0 |
10 |
15 |
6 |
5 |
|||
-0,5 |
|
N0 |
4 |
|
|
N1 |
2 |
|
|
|
|
-1,0 |
|
N2 |
|
|
|
0 |
|
|
|
|
0 |
I0  I1
I1 
I2 
2 |
4 |
Real-valued argument: |
Imaginary-valued argument: |
Jm, Nm |
Km, Im |
Figure C.1: Graph of Bessel functions of types J , K, N , and I, each for index values 1 . . . 3.

Appendix D
Optics with Gaussian Beams
The general public holds the notion of a laser beam as a cylindrical bundle of rays that travels arbitrary distances without any change of its diameter so that it delivers the same power density wherever it hits. Take note, James Bond: There is no such thing as a cylindrical beam. The laws of di raction make sure that any beam with a finite diameter widens as it propagates; the wider the beam starts out, the more gradual is its spreading, but it is always there.
D.1 Why Gaussian Beams?
For the sake of a quantitative description let us consider a Gaussian beam , i.e., a light beam with a transverse distribution of power following a Gaussian bellshaped curve. Such beams are ubiquitous in laser physics; they originate from laser resonators for which the Gaussian profile is the lowest transverse mode. As light is coupled out, one automatically gets a Gaussian beam. The first concise treatment of the situation, still worthwhile reading today, is given in [89]; for a particularly transparent description see [135] or [125].
One might think of a Gaussian beam as created in the following way: Start with a plane wave and send it through an amplitude mask (like a photographic slide). Let the mask have a circularly symmetric gray scale so that a bell-shaped beam is carved out of the plane wave.
Once a beam has a Gaussian profile, it will stay that way. Propagation across free space will change its size, but not the functional form. In other words, the Gaussian is invariant (except for scale factors) under di raction. The reader is reminded that in the far-field limit of di raction, the field distribution acquires a shape given by the Fourier transform of the initial shape. It is well known that the Fourier transform of a Gaussian is again a Gaussian. Therefore, the near field Gaussian profile is preserved in the far field – and not just in the limiting cases, but everywhere in between, too. A Gaussian beam is a di raction-limited beam. It is even better: Among all di raction-limited beams, it is the one with the least change of shape.
In analogy to the quantum mechanic uncertainty relation and thinking of light as a stream of photons, one can multiply the transverse localization error
F. Mitschke, Fiber Optics, DOI 10.1007/978-3-642-03703-0 16, |
269 |
c Springer-Verlag Berlin Heidelberg 2009

270 |
Appendix D. Optics with Gaussian Beams |
(the beam radius) with the transverse photon momentum (a measure of the beam’s divergence) and obtain a product that cannot get arbitrarily small. The minimum product is fulfilled by the Gaussian beam.
If a Gaussian beam is transmitted through common optical elements – lenses, curved mirrors – it will get deformed. Nonetheless it will maintain its Gaussian shape. (This is true if we idealize that the lenses are well centered on the beam.) It takes stronger actions to destroy the Gaussian profile: Nonaxially symmetric elements such as cylindrical lenses render it into an ellipsoid version, which can still be considered a generalization; absorbing elements such as apertures can destroy the Gaussian profile altogether. A knife blade inserted halfway into the beam will alter the beam shape.
D.2 Formulae for Gaussian Beams
It is a convention to take the beam radius w (as in width) as that distance from the axis where the field amplitude is reduced to 1/e of the on-axis value; this is also the radius where the intensity has rolled down to (1/e)2 of its on-axis value.1
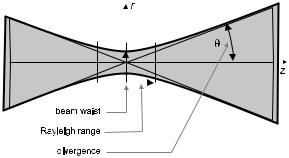
The beam is never cylindrical: Its cross-section varies. At some location the beam has a minimum transverse extent. This is called the beam waist and serves as an important point of reference. Let us identify the propagation direction with the z direction; we conveniently place the zero point at the waist. Then the beam radius is described by
|
|
z |
2 |
|
|
w(z) = w(0) 1 + |
|
|
. |
||
|
|||||
|
|
z0 |
|
|
|
Here z0 is a characteristic length called Rayleigh range. It indicates the distance |
|||||
after which the beam radius has increased by |
√ |
|
and is given by |
||
2 |
|||||
z0 = |
πw2 |
|
|
|
|
0 |
. |
|
|
|
|
|
|
|
|
||
|
λ |
|
|
|
|
As one might have expected, z0 is referred to the only length scale of relevance for wave phenomena, i.e., the wavelength λ.
The Rayleigh range marks the transition from near field to far field: For distances z z0, the beam propagates approximately without change of radius, whereas for z z0 the radius grows in proportion to distance or at a fixed angle. This divergence angle θ is found as
θ = arctg |
w(z) |
≈ |
1 z |
= |
w0 |
= |
|
λ |
||
|
|
w0 |
|
|
|
|
||||
z |
z |
z0 |
z0 |
πw0 |
||||||
with w0 = w(0). The reader should note that for a fixed wavelength θ 1/w0: A beam with wide waist will widen only gradually. Figure D.1 illustrates the relations between w, z, and θ.
As a Gaussian beam propagates and widens, the wavefront does not remain plane. Its curvature can be described by the associated radius, R(z).
|
|
||
R(z) = z 1 + |
|
z0 |
2 . |
|
|||
|
|
z |
|
1Confusingly, in some old texts one can find other conventions, like intensity drop to 1/e.
D.3. Gaussian Beams and Optical Fibers |
271 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure D.1: The contour of a Gaussian beam at r = w(z) takes its narrowest width w0 at the waist (z = 0). In the far field, the beam radius w(z) increases at a fixed angle θ, called the beam divergence.
Obviously,
lim R(z) = ∞ and
z→0
lim R(z) = z.
z→∞
This implies that the wave fronts are indeed plane at the waist; at very large distance they form segments of spheres centered around the waist. At some intermediate distance, the curvature has a minimum: This is the case at z = z0 where R(z) = 2z.
Example
Find the radius of the bright spot on the lunar surface when we aim the beam of a He–Ne laser (λ = 633 nm) at the moon (z = 384, 000 km)!
At w0 = 1 mm, one obtains z0 = 4.96 m and wmoon = 77.4 km; at w0 = 1 m, one gets z0 = 4.96 ×106 m and wmoon = 5.99 m. Lesson learned: In the absence of a beam expansion by way of a telescope, the beam is scattered about as to be undetectable (nearly 80 km), but using a telescope one can illuminate a reasonably small spot of 6 m radius. This allows, e.g., to hit a retro reflector such as placed on the lunar surface by Apollo astronauts and still get a detectable back-reflected signal.
D.3 Gaussian Beams and Optical Fibers
Fibers are waveguides. Indeed, the waves are weakly guided because the index contrast between core and cladding is very small. In this situation, the fundamental mode profile is nearly Gaussian. Consider as a thought experiment that the index di erence shrinks to zero: Then one would expect the same shape as in free space. It is of course simpler to deal with a Gaussian, rather than the complicated composition of Bessel functions described in Chap. 3. Therefore, this approximation is popular and sometimes good enough.
When a beam is coupled from free space into a fiber, one is usually faced with the matching problem between a true Gaussian beam in free space and a less- than-exact almost-Gaussian profile of the fiber’s fundamental mode. (However,
272 |
Appendix D. Optics with Gaussian Beams |
it is usually safe to assume that in a perpendicularly cleaved fiber surface the wave fronts are plane, so that for incoupling as well as outcoupling of light the fiber face can be identified with the position of a beam waist.) The mismatch causes a reduction in coupling e ciency. Even in the presence of ideal lenses without aberrations, this limit cannot be surpassed [120]. Part of the light winds up in the cladding and is eventually scattered out of the fiber, rather than guided in it.
If light propagating inside the fiber is coupled out at the other end and hits a screen at some distance, the pattern on the screen again is similar to a Gaussian. This is because the far-field pattern is the Fourier transform of the near-field pattern as discussed in Sect. 7.4.2 where it was also shown how deviations from the Gaussian pattern can be exploited to gauge the mode profile.
