
- •Случайные события
- •Стохастический мир
- •Случайные величины
- •Совместная и условная вероятности
- •Зависимость и независимость
- •Характеристическая функция
- •Модель аддитивного блуждания
- •Случайные процессы
- •Стохастические уравнения
- •Уравнение Ито
- •Остановка перед восхождением
- •Лемма Ито
- •Точные решения
- •Простые стохастические модели
- •Представление решений
- •Автокорреляция и спектр
- •Порождающий процесс Винера
- •Средние значения
- •Динамическое уравнение для средних
- •Процесс Феллера
- •Логистическое уравнение
- •Вероятности
- •Марковские плотности вероятности
- •Граничные условия
- •Стохастические интегралы
- •Площадь под траекторией Винера
- •Интегралы Ито
- •Интегрирование стохастических уравнений
- •Единственность решений
- •Метод последовательных приближений
- •Системы уравнений
- •Скоррелированные блуждания
- •Системы стохастических уравнений
- •Стохастический осциллятор
- •Линейные многомерные модели
- •Многомерие помогает одномерию
- •Как решать стохастические задачи?
- •Стохастическая природа
- •Теория броуновского движения
- •Стохастический осциллятор
- •Дрожание земной оси
- •Электронный шум
- •Хищники и их жертвы
- •Стохастическое общество
- •Финансовые рынки
- •Эмпирические закономерности
- •Диверсификация
- •Портфель на всю жизнь
- •Опционы
- •Кривая доходности
- •Компьютерное моделирование
- •Статистики
- •Случайные числа
- •Моделирование стохастических процессов
- •Ошибки вычислений и ускорение сходимости
- •Вычисление средних
- •R: Стохастический справочник
- •Основные соотношения теории
- •Системы уравнений с одинаковым шумом
- •M: Математические приложения
- •H: Помощь
- •C: Примечания
- •Рекомендуемая литература
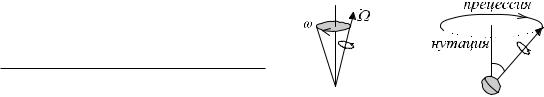
190 |
Глава 7. |
7.3Дрожание земной оси
Наша Земля, несмотря ни на что, вращается вокруг своей оси с периодом, равным примерно 24 часа. Если ночью в хорошую погоду длительное время смотреть на зв¼здную сферу у нас над головой, видно, что она поворачивается вокруг некоторой точки в окрестности Полярной звезды (в северном полушарии). Именно туда направлена мгновенная ось вращения Земли.
Если бы наша планета была абсолютно тв¼рдым телом, то е¼ динамика подчинялась бы уравнениям Эйлера. Выберем систему отсч¼та, жестко связанную с Землей, направив ось z к северному полюсу, а x и y располо-
жив в плоскости экватора. В первом приближении Земля представляет собой симметричный эллипсоид (шар, несколько сплюснутый вдоль оси z). Поэтому е¼ моменты инерции, вычисленные в этой системе, равны
Jz = J1 = 2Mr22=5 è Jx = Jy = J2 = M(r12 + r22)=5, где M масса Земли, а ri радиусы эллипсоида в направлении к полюсу r1 и в экваториальной плоскости r2. Уравнения Эйлера для свободного вращения имеют вид:
8 J2 |
_ |
J2) z y = 0 |
_ x + (J1 |
||
J1 |
z = 0 |
J1) z x = 0: |
< J2 |
_ y + (J2 |
|
: |
|
|
Вектор = f x; y; zg это угловая скорость вращения. Она направлена вдоль мгновенной оси вращения и по модулю равна = d =dt повороту на малый угол d за время dt. Проекции вычислены в си-
стеме отсч¼та, связанной с Земл¼й. Поэтому, когда мы находимся на е¼ поверхности, положение наблюдаемого центра зв¼здной сферы зада¼тся .
Первое уравнение системы приводит к постоянству проекции угловой скорости z = const. Два вторых являются осцилляторными и имеют периодические решения:
8 |
y = A sin(!t) |
z |
|||
|
x = A cos(!t) |
|
|||
< z = const |
2) |
23o |
|||
:= z ( |
1 |
J |
2 |
||
! |
J |
|
=J |
|
|
Таким образом, вектор вращается по поверхности конуса с угловой ча- стотой !. Подобное вращение мы наблюдаем, запуская детский волчок,
который, быстро вращаясь вокруг своей оси, одновременно медленно поворачивает ось вращения по поверхности конуса.

Стохастическая природа |
191 |
Обычно различают два типа вращения мгновенной оси. Медленное с большой амплитудой это прецессия. Дополнительные небольшие периодические возмущения этого движения это нутация.
Для Земли M = 5:976 1024 êã, r1 = 6356:8 êì, r2 = 6378:2 êì. Ïåðè-
од вращения вдоль главной оси соответствует 24 часам, поэтому z = 2 =24 = 7:27 10 5 c 1. Òàê êàê (J1 J2)=J2 = (r22 r12)=(r22 + r12) = 1=298, то прецессионный период составляет примерно 300 дней и был предсказан ещ¼ Эйлером. Земной наблюдатель должен наблюдать прецессию (нутацию), как медленное перемещение центра вращения небесной сферы по окружности относительно неподвижных зв¼зд. Такое изменение положения земной оси впервые обнаружил астроном Чандлер в 1891 г.
Однако наблюдаемое движение вращения земной оси оказывается существенно сложнее и носит стохастический характер. Координаты x =
x è y = y являются угловыми (направление !), однако, так как их колебания очень невелики, можно считать, что ось вращения на поверхности Земли рисует вокруг северного полюса соответствующую кривую. Для перехода к метрам углы в радианах необходимо умножить на радиус Земли. Если устранить очень медленную трендовую составляющую (вековое движение), колебания по x и y выглядят следующим образом:
|
|
|
|
1960 |
2010 |
0.25 |
y |
|
0.2 |
x |
|
|
|
|
0 |
|
|
|
|
x |
-0.2 |
|
|
0 |
|
|
|
y |
|
-0.25 |
0 |
0.25 |
|
||
|
|
|
0.2 |
|
|
|
|
|
0 |
|
|
-0.25 |
|
|
-0.2 |
|
|
|
|
|
|
|
|
Слева представлено движение проекции Земной оси (arcsec) 2000-2008 (точки ежедневные наблюдения), а справа отдельно по каждой оси
за период 1960-2008. Максимальное отдаление от оси составляет около 0.3 arcsec (1arcsec=4:848 10 6 rad). Поэтому на поверхности Земли это
приводит к максимальному радиусу 9 м. В среднем он раза в два меньше.
Спектральный анализ показывает, что эти колебания являются суммой двух гармоник с периодом 365 дней и 433 дня. Первая периодич- ность совпадает с длительностью года. Вторая оказывается квазипериодической. Амплитуда первой гармоники около 0.09, а второй 0.15.
192 |
|
|
|
|
|
|
|
|
|
|
|
Глава 7. |
|
Наблюдаемые периодические колебания амплитуды (биения) связаны |
|||||||||||||
со сложением этих двух гармоник. Так, например, если колебания имеют |
|||||||||||||
различную частоту !1 è !2 и одинаковые амплитуды, их сумма равна: |
|||||||||||||
A cos(! |
t) + A cos(! t) = 2A cos |
!1 !2 |
t |
cos |
|
!1 + !2 |
t |
: |
|||||
|
|
1 |
|
|
2 |
|
2 |
|
2 |
|
|
||
Åñëè !1 !2, то первый множитель имеет большой период измене- |
|||||||||||||
ния амплитуды |
колебаний со средней частотой (!1 + !2)=2 (второй |
||||||||||||
множитель). Результирующая периодичность биений составляет 6.35 лет |
|||||||||||||
((1=365 |
|
1=433) 1). |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x2 + y2: |
|
|
|||
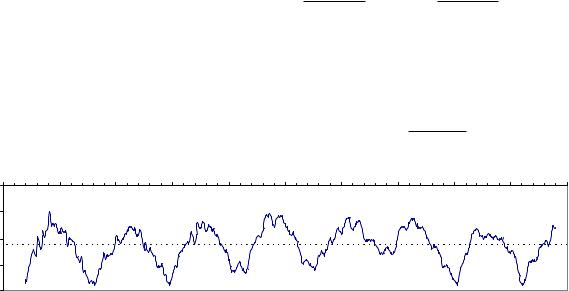
Привед¼м динамику расстояния от центра r = |
|
|
|||||||||||
|
|
|
|
|
1980 |
1985 |
1990 |
|
1995 |
|
|
|
|
1960 |
1965 |
1970 |
1975 |
|
|
|
|
p |
|
2000 |
2005 |
2010 |
|
0.3 <r>=0.17 |
|
|
|
|
|
|
|
|
|
|
|
||
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее значение hri = 0:17. Хорошо видно, что биение не является |
|||||||||||||
строго периодическим, а носит стохастический характер. |
|
|
|||||||||||
Одна из наиболее простых моделей чандлеровских колебаний была |
|||||||||||||
предложена Колмогоровым. Уравнения Эйлера можно переписать в сле- |
|||||||||||||
дующем виде: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
d x = |
! y dt |
|
|
|
|
|
|
|
|
|
|
|
|
d y = ! x dt; |
|
|
|
|
|
|
||
ãäå ! = z (J1 J2)=J2. Земля не является абсолютно тв¼рдым телом. |
|||||||||||||
Климатические движения масс воды, землетрясения и другая внутрен- |
|||||||||||||
няя активность приводят к постоянному изменению тензоров инерции. |
|||||||||||||
В результате потери энергии на преодоление вязкости (пластичности |
|||||||||||||
Земли) ось вращения рано или поздно оказалась бы совмещ¼нной с осью |
|||||||||||||
симметрии и никакой нутации не было бы. Введ¼м затухание нутации |
|||||||||||||
с параметром и стохастические изменения оси вращения в результате |
|||||||||||||
активности Земли. Обозначим x = x, y = y и запишем уравнения |
|||||||||||||
стохастического осциллятора: |
|
|
|
|
|
|
|
|
|||||
dx = ( x ! y) dt + Wx dy = (+! x y) dt + Wy:
Их математические свойства мы подробно изучали в разделе x6.3, ñòð.
160. В частности, после затуханpèя возникает квазипериодическое движение с типичным радиусом = и частотой !.

Стохастическая природа |
|
|
|
|
|
|
|
|
|
|
|
|
|
193 |
|
||
Íàéä¼ì, êàê âåä¼ò ñåáÿ |
|
|
2 |
|
|
2 |
|
|
r = p |
|
|
|
|
|
|||
|
|
|
|
|
|
x |
2 |
+ y |
2: |
||||||||
|
|
|
|
расстояние от начала координат |
|
|
|
||||||||||
|
@x |
= r |
y |
; |
@x2 |
= r3 |
xy |
x2 |
: |
|
|
|
|
|
|
||
|
@r |
1 |
x |
|
|
@ r |
1 |
y |
|
xy |
|
|
|
|
|
|
|
При помощи формулы Ито получаем следующее уравнение:
|
2 |
|
|
|
dr = |
|
r dt + |
|
(x Wx + y Wy): |
2r |
r |
|||
Стохастический член можно выразить через одномерную винеровскую переменную:
x Wx + y Wy |
|
x "x + y "y |
p |
|
= "p |
|
= W: |
|
= |
dt |
dt |
||||||
r |
|
|||||||
|
r |
|||||||
Действительно, если мы решаем уравнение итерациями, какие бы ни были значения x, y к некоторому моменту времени, сумма независимых от них гауссовых чисел "x, "y снова да¼т гауссово число. Так как x2+y2 = r2, то оно имеет единичную дисперсию. В результате, для радиуса можно записать одномерное уравнение рэлеевского типа:
|
2 |
|
|
|
|
|
|
dr = |
|
r dt + W: |
|
|
|
||
2r |
|
|
|
||||
|
|
|
p |
|
|
||
Снос уравнения имеет равновесную точку |
r1 |
= = |
2 |
, в которой об- |
|||
|
|
|
|
|
|||
ращается в ноль. Если расстояние от начала координат существенно больше r1, то детерминированная часть динамики начинает уменьшать радиус, и наоборот. Поэтому r совершает характерные стохастические колебания вокруг этого равновесного положения.
Так как решения для x(t) и y(t) известны, мы автоматически имеем
точное решение рэлеевского уравнения, выраженное через две случайные гауссовы величины. В асимптотическом пределе, который мы наблюдаем при изучении вращения Земли, радиус колебаний оси равен:
2 q
r = p "2x + "2y:
2
p p
В частности, среднее значение радиуса составляет r = =2 .
На самом деле, модель Колмогорова является очень упрощ¼нной имитацией стохастических колебаний. В частности, в ней присутствует только одна периодическая компонента, и, как следствие, нет наблюдаемых биений с периодом в 6.35 лет.
