Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Астраханский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matanaliz

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 3233 / 3333

322 Лекция 22. Функциональные ряды

Разложение в ряд будет иметь вид

'(z) = a0 + X1 ancosnz + bnsinnz:

2 n=1 Из (22.10)-(22.12) получим

z =

¼x

dz =

a =

'(z)dz =

z = l¼,, x = ll

Z f(x)dx

bn = ¼

'(x)sinnzdz =

z =

l¼,,

x =

¯ = l

Z f(x)sin l

z =

¼x

dz =

¼x

dx:

an = ¼ Z

'(z)cosnzdz = l Z f(x)cos l

¡¼

¡l

Ряд Фурье примет вид

n¼x

f(x) =

+ bnsin

ancos

n=1

22.4.Контрольные вопросы

1.Сформулируйте понятие равномерной сходимости функционального ряда.

2.При каких условиях сумма функционального ряда является непрерывной функцией?

3.При каких условиях функциональный ряд можно почленно интегрировать?

4.При каких условиях функциональный ряд можно почленно дифференцировать?

5.Как определяется область сходимости степенного ряда?

6.Выведите формулы для определения коэффициентов ряда Фурье.

22.5. Методические указания по решению примеров

Пример 22.3. Найти область сходимости ряда

22.5. Методические указания по решению примеров

323

5n+1

n !

¢ x

Решение. Найдем радиус сходимости ряда

R = n!1

¯an+1

n!1

n¢!

5n+2

n!1

5n+1

(n + 1) !

n + 1

lim

= lim

= :

Интервалом

¯сходимости¯

ðÿäà¯

является вся¯

числовая ось.

Пример 22.4. Найти область сходимости ряда

n=1

Решение. Находим радиус сходимости

(n + 1) 3n+1

n + 1

Интервал сходимости:

3; 3 .

n!1

R = n!1

¯an+1

n!1

n ¢

3¢n

lim

¯(

)

= 3 lim

= 3:

= lim

¯¡

Исследуем ряд на концах интервала. При x = 3 получаем

гармонический ряд

, который расходится. При x = ¡3 ïîëó-

(

1)n

Лейбницы имеем:

чаем знакочередующийся ряд

. На основании признака

1 >

> ¢¢¢

;

2 >

3 >

lim

= 0:

n!1 n

Оба условия выполняются, следовательно, ряд сходится. Таким образом, область сходимости ряда является полусегмент [¡3; 3).

Пример 22.5. Найти область сходимости функционального

ðÿäà	1	(n + 1)5 ¢ x2n :
	X
	n=1	2n + 1
	n=1

Решение. Исследуем сходимость получившегося числового ряда

по признаку Даламбера.

lim

un+1

= lim

(n + 2)5

x2n+2

(2n + 1)

= x 2

(2n + 3)¢

¢1)5 x2n

½ = n!1

j j ¢

n!1 ¯

(n +

n +¯

2n +

lim

³n + 1´

¢ 2n + 3

¢ n!1

j j

Ряд сходится, если jxj2 < 1, откуда ¡1 < x < 1.

11*

324 Лекция 22. Функциональные ряды

Исследуем сходимость ряда на концах интервала сходимости. При x = §1 функциональный ряд принимает вид

1	(n + 1)5		1	(n + 1)5
X		(§1)2n =	X		:
n=1	2n + 1		n=1	2n + 1

Этот числовой ряд расходится, т.к. не выполняется необходимый признак сходимости: lim (n + 1)5 = 1 6= 0. Поэтому область

n!1 2n + 1

сходимости данного рада x 2 (¡1; 1).

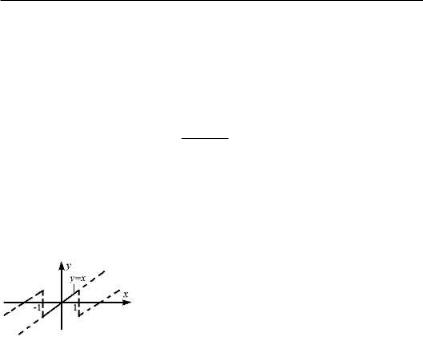
Пример 22.6. Разложить в ряд Фурье функцию y = x íà

интервале (¡1, 1)

Заданная функция не является периодической. Поэтому формируем новую функцию, которая на интервале (¡1, 1) должна

совпадать с исходной функцией (рис.22.1)

Введенная функция является нечетной, поэтому в разложении коэффициенты a0, an будут нулевыми. Определим

коэффициенты bn

Ðèñ. 22.1.

v =

u = x, du = dx

n¼

sinn¼xdx,

bn =

xsinn¼xdx =

dv = cosn¼x

xcosn¼x

= ¡

¡1

n¼

+ n¼ Z1 cosn¼xdx =

n+1

Разложение функции y = x на интервале¯

(-1, 1) будет иметь

= n¼

(¡1)

+ n2¼2 sinn¼x

¡1 = n¼

(¡ )

âèä

n+1

f(x) =

n¼

(¡1)

sinn¼x:

n=1

22.6. Примеры для самостоятельного решения

Найти область сходимости ряда.

Разложить функцию на заданном интервале в ряд Фурье: 22.6.1. . Ответы. 1. x > 0, 5;для х>1 ряд сходится абсо-

лютно, а для 0,5<x 61условно. 2. ряд сходèòñÿ в единствåííîй точке õ =0. 3. сходится абсолютно для ¡pe ¡ 1 < x < pe ¡ 1 .

22.6. Примеры для самостоятельного решения

325

(¡1) n

1 (nx)¡n:

1. n=1 n2x¡1

n=1

1 lnn

1 + x2

3 ¡ x2

³2 ´

(x + 2)n

P ¡

+ xn

n=1 1

n=1 3 nx

nP1

10. n=1

11.

(¡1)n

12. 2ntg

2n sin x

n=1 xnn ln n

n=1

P1 x2n

13.

n(n + 1)

14.

n=1

n .

1 x

n=1

16. 1 (nx)n

15.

=1(nx)

17. (x ¡ 4)n

18. (x + 1)n

19.

y(x)

24.

y(x) = sin ax,

¡¼ <

= sign x,

(¡¼ < x < ¼).

< x < ¼,

целое число.

20.

y(x)

a ¡ íå

®x

25. y(x) = e , ¡h < x < h

A, åñëè 0 < x < l;

= ½ 0, åñëè 0 < x < 2l,

А>0 постоянная.

21. y(x) = x, ¡¼ < x < ¼

26.

y(x) = x sin x,

¡¼ <

< x < ¼

22. y(x) =

¼ ¡ x

, 0

< x <

27.

y(x) = x cos x,

¼ <

< 2¼

< x < ¼

23. y(x) = jxj , ¡¼ < x < ¼

28. y(x) = sign(cos x)

4.сходится

абсолютно

äëÿ

< x < ¡ 2

< x <

5.сходится абсолютно для x < ¡1. 6. сходится абсолютно для ¡4 < x < 0и условно в точке x = ¡4. 7. сходится абсолютно для |x|>1. 8. x>1 è x 61; äëÿ |x|>1 сходится абсолютно, а при

326 Лекция 22. Функциональные ряды

x = 1 условно. 9. абсолютно сходится для |x|>1. 10. сходится абсолютно 2¼k < x < (2k + 1)¼, ãäå k 2 Z. 11. ¡1 < x < ¡1 è

1 6 x < 1; в точке x =1

сходимость условная. 12. сходится аб-

/2, ãäå n 2 N, k 2 Z.13.[¡1; 1].

солютно при всех x 6= ¼(2k + 1)

14. (¡1; 1).

15.

x = 0.

16.

17. [

3; 5 . 18.

(¡1; +1).

¡e ; e .

)

Pn+1

k ¡

2 ´

sin(

1)x

sin(2k + 1)¼x

19. ¼ k=1

2k ¡ 1 ; 20.

¼ k=0

2k + 1

l .21.

sin nx

cos(2k + 1)x

2 n=1

)

n . 22. n=1

n .23. 2 ¡

(¡

¼ k=1 (2k + 1)2 . 24.

½n=1

¾.

2 sin ¼a

(

1)n+1n sin nx

(¡1)

25. 2sh (ah) 2a

+ ::: ::: + n=1

(ah)2 + (¼n)2

1¡

ah cos

n¼x

¼n sin

n¼x

n+1

1 2

26. 1

1 cos x + 2

(¡ )

cos nx.27. 16

(¡ )

n sin2 nx

cos(

n=2 n2 ¡ 1

¼ n=1

4n2 ¡ 1

(¡ )

k +

28. ¼ =0

(2k + 1)

СПИСОК ЛИТЕРАТУРЫ

1. Ильин В. А., Позняк Э. Г. Основы математического анализа.М:

Наука. 1998.

2. Петрушко И. М. (ред) Курс высшей математики. Введение в анализ. Дифференциальное исчисление. СПб. Лань. 2008.

3. Петрушко И. М. (ред) Курс высшей математики. Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения. СПб. Лань. 2008.

4. Фихтенгольц Г. М. Курс дифференциального и интегральнлго исчисления. Т. 1. СПб. Лань. 2009.

5. Кудрявцев Л. Д. Математический анализ. Т. 1. М: Вычшая школа. 1998.

6. Берман Г. Н. Сборник задач по курсу математичекого анализа. М: Наука. 1985.

7. Цыкунов А. М. (ред.) Сборник задач по высшей математике. Астрахань. Изд. АГТУ. 2008.

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 3233 / 3333

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.04.2015590.18 Кб18L_r_OpenOffice_org_Impress_samostoyatelno.pdf
#
12.04.20151.56 Mб48makeeva3английсский тех перевод.pdf
#
12.04.20153.28 Mб10Manual.pdf
#
26.09.2019108.03 Кб6marketing_ekzamen.doc
#
11.11.2019231.42 Кб5Markets Дроздова.doc
#
15.03.20161.91 Mб18matanaliz.pdf
#
12.04.20151.18 Mб33matrialka_otvety.docx
#
19.11.2019851.43 Кб14meeting people (2).docx
#
12.04.2015648.06 Кб17mehanika1980.pdf
#
12.04.2015424.45 Кб98MEKhANIKA_FIZIKA.doc
#
12.04.20153.21 Mб6MetodDB.pdf