
matanaliz
.pdf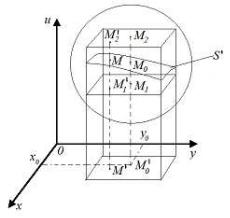
132 |
|
Лекция 9. Неявные функции и условный экстремум |
|
|
|
|
|
|||||||||||||
u = ¡ 1 ¡ x2 ¡ y2 . |
|
|
|
u = p |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
¡ x |
|
|
¡ y |
|
|
|
|
|
|||||||||
решимо и определяет явную функцию |
|
|
|
1 |
|
2 |
|
2 |
|
èëè |
||||||||||
|
p |
|
|
M |
|
(o x |
|
y) |
|
|
x |
|
+ y |
|
|
= |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Если же на сфере взять точку |
|
1 |
|
, |
, |
|
, ãäå |
|
|
2 |
|
|
2 |
|
1, |
||||
то окрестность этой точки не может однозначно быть спроецирована на плоскость xoy, так как часть окрестности находится
âверхней полусфере, а другая часть в нижней. Следовательно, уравнение (9.2) не является однозначно разрешимым0 в этой окрестности. При этом частная производная Fu = 0 в точке M1.
Теорема 9.1. Пусть функция F (u, x, y) дифференцируема
âнекоторой окрестности точки M0 (u0, x0, y0) 2 R3 è ÷àñò-
ная производная |
|
@F |
непрерывна в точке M0. Тогда, если |
|
|
@u |
|||
F (u0, x0, y0) = 0, |
@F |
6= 0, то для любого достаточно малого |
||
@u |
||||
" > 0 найдется окрестность точки N (x0y0) 2 R2 такая, что в
пределах этой окрестности существует единственная непрерывная и дифференцируемая функция u = f (x, y), удовлетво-
ряющая условиям: ju ¡ u0j < ", F (u, x, y) = 0:
|
ë |
|
Ä |
î |
ê |
à |
ç |
à |
ò |
å |
|
|
ü |
ñ ò |
â |
о. Уравнение |
|||||||
|
F (u, x, y) = 0 в простран- |
||||||||||
|
стве R3 определяет неко- |
||||||||||
|
торую поверхность S0. Ïðè |
||||||||||
|
ýòîì F (M0) = 0 ïî óñëî- |
||||||||||
|
вию, т.е. точка M0 лежит |
||||||||||
|
на поверхности S0. |
|
|
|
|
||||||
|
ñòè |
Áåç |
потери |
общно- |
|||||||
|
|
будем |
считать, |
÷òî |
|||||||
|
Fu0 |
(M0) > |
0:Тогда |
|
èç |
||||||
|
непрерывности |
F 0 (M0) |
è |
||||||||
|
|
|
|
|
|
|
u |
|
|
|
|
|
теоремы |
îá |
устойчивости |
||||||||
|
знака непрерывной |
ôóíê- |
|||||||||
Ðèñ. 9.2. |
ции следует, что найдется |
||||||||||
окрестность |
точки |
Ì |
, |
||||||||
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
â |
|
которой |
Fu(M0) > 0. |
|||||||
Возьмем в качестве такой окрестности шар достаточно малого |
|||||||||||
радиуса с центром в точке M0:. |
|
|
|
|
|
|
|
|
|
|
|
Впишем в шар правильный прямоугольный паралле- |
|||||||||||
лепипед высотой 2" с ребром основания равным 2± ñ |
|||||||||||
центром в точке M0, и рассмотрим функцию одной пере- |
|||||||||||
менной F (u, x0, y0) ïðè |
фиксированных |
x0, y0 |
íà |
сегменте |
|||||||
[u0 ¡ ", u0 + "] : Учитывая равенство F (u0, x0, y0) = 0, Fu0 |
(M0) > |
||||||||||
|
9.2. Неявные функции |
133 |
> 0, получим, |
÷òî F (M2) > 0, F (M1) < 0, |
где точки |
M2 (u0 + ", x0, y0) , |
M1 (u0 ¡ ", x0, y0) лежат на |
верхней и |
нижней гранях параллелепипеда соответственно, но тогда на этих гранях функции F (u0 + ", x0, y0) > 0, F (u0 ¡ ", x0, y0) < 0
при достаточно малых ± в силу непрерывности функции
F (u, x, y) и теоремы о сохранении знака, но тогда получаем неравенства
jx ¡ x0j < ±, jy ¡ y0j < ± ) ju ¡ u0j < " : |
(9.3) |
Теперь возьмем в качестве окрестности точки M (x0y0) проекцию
нижней грани параллелепипеда на плоскость xOy: Тогда будут выполнены условия
jx ¡ x0j < ±, jy ¡ y0j < ±: |
(9.4) |
Зафиксируем произвольные точки x è y в этом квадрате и рассмотрим снова функцию одного аргумента F (u, x, y) на сегменте
[u0 ¡ ", u0 + "], но на верхней грани F (u0 + ", xy) > 0, à íà
нижней грани F (u0 ¡ ", xy) < 0, à Fu0 в шаре положительна, т.е. функция F (u, x, y) в параллелепипеде возрастает, но тогда внут-
ри сегмента u0 ¡ " 6 u 6 u0 + " найдется единственная точка, где
F (u, x, y) = 0, а такой точкой является M0. Из изложенного вы- текает, что часть поверхности S0, вырезанная параллелепипедом
однозначно проектируется на плоскость xOy в виде квадрата,
определяемого неравенствами (9.4). Следовательно, существует единственная функция u = f(x, y), удовлетворяющая условию
ju ¡ u0j < " при выполнении (9.4) и являющаяся решением уравнения F (u, x, y) =
из (9.4) следует ju ¡ u0j < ". Остается доказать дифференцируемость функции f(x, y).Так как по условию F (u, x, y)- дифферен-
цируема, то выражение для полного дифференциала в точке M0 будет иметь вид
dF = Fu0 du + Fx0 dx + Fy0dy = 0: |
(9.5) |
||||
По условию теоремы F 0 (u0, x0, y0) = 0, и функция |
F (u, x, y) |
||||
дифференцируема, тогда u |
6 |
|
|
||
du = ¡ |
Fx0 |
dx ¡ |
Fy0 |
(9.6) |
|
|
|
dy: |
|||
Fu0 |
Fu0 |
||||
Следовательно, функция u = f(x, y) дифференцируема, кроме
того, из (9.6) следуют формулы для вычисления частных произ- |
|||||||||||
водных |
@u |
= ¡ |
Fx0 |
, |
@u |
= ¡ |
Fy0 |
: |
(9.7) |
||
|
@x |
Fu0 |
|
@y |
|
Fu0 |
|||||
134 |
Лекция 9. Неявные функции и условный экстремум |
Следует |
отметить, что поверхность S или плоская кривая L, |
заданные уравнениями F (u, x, y) = 0 F (x, y) = 0 могут иметь
особые точки, где теорема неприменима. К особым точкам относятся точки,0 где все частные производные равны нулю, а также точки, где Fu = 0, что уже было продемонстрировано на примере со сферой, когда не существует окрестность точки, которую можно было бы однозначно спроектировать на плоскость xOy, à
у плоской кривой на ось Ox èëè Oy.¤
Рассмотрим естественное обобщение приведенной теоремы |
||||||||||||
на неявные функции, определяемые системой функциональных |
||||||||||||
уравнений. Предположим, что k функций |
|
|
|
|
|
|||||||
ui = fi(x1, ... , xm) |
i = 1, ... , k: |
|
(9.8) |
|||||||||
ищутся как решение k функциональных уравнений |
|
|||||||||||
Fi(u1, ... , uk, x1, ... , xm) = 0 |
i = 1, ... , k: |
(9.9) |
||||||||||
Составим определитель Якоби (Якобион) для функций Fi |
||||||||||||
|
D(F1, ... , Fk) |
¯ |
@u1 |
¢¢¢. |
|
@uk |
¯ |
(9.10) |
||||
|
|
|
|
= ¯ |
@F1 |
|
|
|
|
@F1 |
¯: |
|
¢ = |
|
|
|
|
|
. |
. . |
|
||||
|
D(u1, ... , uk) |
|
|
|
||||||||
|
|
¯ . |
|
|
¯ |
|
||||||
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
|
|
|
|
|
¯ |
|
|
|
|
|
|
¯ |
â íåêî- |
Теорема 9.2. Пусть функций (¯9.9) дифференцируемы¯ |
||||||||||||
|
|
|
|
¯ |
@Fk |
|
|
@Fk |
¯ |
|
||
|
|
k |
¯ |
@u1 |
¢¢¢ |
|
@uk |
¯ |
|
|||
|
|
|
|
¯ |
|
¯ |
|
|||||
торой окрестности точки M0(u0 |
, ... , u00 , x0, ... , x0 |
0 ) |
2 R |
m£k, |
||||||||||||||||
имеют |
|
частные |
производные |
10 |
ïî |
|
k |
1 |
|
|
m |
|
|
|
||||||
|
|
|
|
переменным u1, ... , uk, |
||||||||||||||||
непрерывны в точки M0 и Якобиан |
D(F1, ... , Fk) |
6= 0. Тогда для |
||||||||||||||||||
D(u1, ... , uk) |
|
|||||||||||||||||||
достаточно малых "i > 0, i = 1, ... , k найдется окрестность |
||||||||||||||||||||
точки |
|
0, ... , |
0 |
|
m такая, |
|
÷òî |
в пределах |
ýòîé |
|||||||||||
|
N0(x1 |
xm) 2 R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
окрестности существуют единственные k функций (9.8), |
||||||||||||||||||||
которые |
являются непрерывными, |
|
дифференцируемыми |
è |
||||||||||||||||
выполнены неравенства |
|
0 |
|
< "i |
, |
i = |
1, ... , |
k |
. |
|
|
|
|
|
||||||
ui ¡ ui |
|
|
|
|
|
|
|
|
|
|
||||||||||
Доказательство можно¯ |
осуществить¯ |
методом математической |
||||||||||||||||||
индукции, используя предыдущую¯ ¯ |
теорему. |
|
|
|
|
|
|
|
|
|
||||||||||
Как следствие этой теоремы можно привести теорему о вза- |
||||||||||||||||||||
имно однозначном отображении двух множеств m¡мерного про- |
||||||||||||||||||||
странства. |
некоторой окрестности точки |
M0 |
2 Rm |
m |
||||||||||||||||
Рассмотрим в |
||||||||||||||||||||
функций ui = fi(x1, ... , xm), i = 1, ... , m, которые осуществляют отображение указанной окрестности на некоторое множе-

9.3. Условный экстремум |
135 |
ñòâî m¡мерного пространства переменных ui, i = 1, ... , m. Тогда справедливо следующее утверждение.
Теорема 9.3. (о взаимно однозначном отображении). Åñëè функции ui = fi(x1, ... , xm), i = 1, ... , m дифференцируемы в
окрестности точки M0 и все частные производные непре-
рывны в самой точке M0, а Якобиан |
D(F1 |
, ... , Fk) |
|
|
|
D(u1 |
, ... , uk) отличен |
||||
|
|||||
от нуля, то функции осуществляют взаимно однозначные |
|||||
отображения некоторой окрестности точки M0(x0 |
, ... , x0 ) |
||||
на некоторую окрестность точки M0(u0, ... , u0 ). |
1 |
m |
|||
1 m
Справедливость утверждения следует из предыдущей теоремы. Действительно, функции ui = fi(x1, ... , xm) можно рассматривать как систему функциональных уравнений относительно xi, i = 1, ... , m, для которых выполнены условия предыдущей
теоремы, а следовательно в некоторой окрестности точки N0
имеется единственное решение xi = 'i(u1, ... , um), i = 1, ... , m. Следует отметить, что в условиях утверждения прямое отображение ui = fi(x1, ... , xm) и обратное xi = 'i(u1, ... , um) ÿâëÿ-
ются непрерывными.
9.3. Условный экстремум
Мы уже познакомились с необходимыми и достаточными условиями наличия экстремумов в области определения функции нескольких переменных. Вместе с тем часто встречается задача об отыскании экстремумов функции при некоторых дополнительных условиях, ограничивающих область изменения аргументов. Например, требуется найти экстремум функции u = x2 + y2
при условии x + y ¡ 1 = 0, т.е. экстремум заданной функции
ищется не на всей области определения функции, а лишь на прямой x + y = 1. Эти дополнительные условия часто называ-
ют уравнениями связи или ограничениями. Для решения сформулированной задачи выразим переменную из уравнения связи y = 1 ¡ x и подставим это значение в уравнение функции
u = (1 ¡ x)2 + x2. Таким образом, задача поиска условного экс-
тремума сведена к задаче определения безусловного экстремума |
|||||||||||||
|
du |
= 4(x |
|
1) = 0 |
|
x = 1 |
, y = 1. В точке с координатами |
||||||
|
|
|
|
|
|
||||||||
:dx1 |
¡ |
) |
|||||||||||
1 |
|
|
2 |
2 |
2 |
||||||||
|
|
; |
|
|
|
функция имеет условный экстремум минимум, хотя |
|||||||
2 |
2 |
|
|||||||||||
при отсутствии ограничений минимум функции находится в точ- |
|||||||||||||
³ |
|
|
|
|
´ |
|
|
|
|
|
|
||
êå (0;0).


138 |
Лекция 9. Неявные функции и условный экстремум |
Решение: Заданная область определения является треугольником. Ищем критические точки, решая систему уравнений
8< @x@z = 2x ¡ y + 1 = 0, : @y@z = 2y ¡ x + 1 = 0,
x = ¡1, y = ¡1: Получили точку M1(¡1, ¡1), которая принадлежит заданной области, z(M1) = ¡1. Исследуем функцию на границе, состоящей из трех прямых. 1. x = 0, y 2 [¡3; 0]. Íà
этой прямой z = y2 + y. Получили задачу поиска наибольшего и
наименьшего значений для функции одной переменной, заданной на сегменте. Решаем уранение dydz = 2y + 1 = 0. Получаем точку
M2(0; ¡1=2), которая лежит на границе. Кроме того имеем точки на границе сегмента M3(0; ¡3), M4(0; 0). Вычисляем значения функции в этих точках z(M1) = ¡1=4, z(M3) = 6, z(M4) = 0. 2.
y = 0, x 2 [¡3; 0]. На этой прямой z = x2 + x Решаем уранение
dxdz = 2x + 1 = 0. Получаем точку M5(¡1=2; 0), которая лежит на границе. Кроме того имеем точку на границе сегмента M6( ¡
¡3; 0): Точка (0; 0) уже исследована. z(M5) = ¡1=4, z(M6) = 6. 3. Исследуем функцию на прямой x + y = ¡3. Определив из
этого уравнения
y = ¡x ¡ 3, получим z = 3x2 + 9x + 6: Решаем уравнение
|
dz |
= 6x + 9 = 0, в результате получаем точку M7( ¡3=2; ¡ |
|
|
dx |
||
¡3=2), |
|
||
z(M7) = ¡3=4 Сравнивая полученные значения функции, по- |
|||
лучаем sup z (M) = z (M3) = z (M6) = 6, |
inf z (M) = z (M1) = |
||
|
|
M Q |
M2Q |
2 |
|
||
=¡1.
2.Найти призводную dxdy от фунуции, заданной в неявной
форме
x3y ¡ y3x = 16:
Решение: Если функция задана в виде F (x, y) = 0, то производная dxdy определяется по вормуле (9.5)
dy = ¡Fx0 : dx Fy0

9.5. Примеры для самостоятельного решения |
139 |
||||||
В данном случае F (x, y) = x3y ¡ y3x ¡ 16. Тогда получим |
|
||||||
|
dy |
= |
3x2y ¡ y3 |
= |
y3 ¡ 3x2y |
: |
|
|
|
|
|
||||
dx |
¡x3 ¡ 3y2x |
|
x3 ¡ 3y2x |
|
|||
3. Найти условный экстремум функции z = x2 ¡ y2 при наличии
ограничений y ¡ 2x = ¡6.
Решение: Решаем задачу путем преобразования, позволяющего получить задачу поиска безусловного экстремума. Из заданного условия имеем y = 2x ¡ 6. В результате получаем фунук-
öèþ0 |
одной пременной z = ¡3x2 + 24x ¡ 36: Решаем уравнение |
||||
z = |
0, |
6 |
24 = 0, откуда получаем x = 4, y = 2: В точке |
||
¡ x + |
|
00 |
= ¡6. Следовательно это точка условного |
||
M(4; 2) |
имеем z |
|
|||
максимума.
9.5. Примеры для самостоятельного решения
Определите наименьшее и наибольшее значения функций в замкнутой области, ограниченной линиями .
1. z = x2 + 2xy ¡ y2 ¡ 2x + 2y, Q : y = x + 2, y = 0, x = 2.
2. z = x2 + 2xy ¡ 4x + 8y, Q : y = 0, y = 2, x = 0, x = 1.
3. z = x3 + y3 ¡ 3xy, Q : y = ¡1, y = 2, x = 0, x = 2. 4. z = 2x3 + 4x2 + y2 ¡ 2xy, Q : y = x2, y = 4.
Определить условные экстремумы функций.
5. z = xy2, x + y = 4: 6. z = x2 + y, x + y = 4:
7. z = x2 + y2 + x ¡ y, x + y = 4: 8. z = xy, x2 + y = 12:
|
9.5.1. |
Ответы. |
1. |
Наименьшее значение z(1, 0) = ¡1; |
|||
наибольшее |
значение |
z(2, 3) = 9. |
2. |
Наименьшее |
значе- |
||
íèå |
z = (1, 0) = ¡3; |
наибольшее |
значение z = (1, 2) = 17. |
||||
3. |
Наименьшее значение |
z = (0; ¡1) = z(1; 1) = ¡1; |
íàè- |
||||
большее значение z(2; ¡1) = 13. |
4. |
наименьшее значение |
|||||
z = (0; 0) = 0; наибольшее значение z(¡2; 4) = z(2; 4) = 32. 5.
zmin(4; 0) = 0, zmax(4=3; 8=3) = 256=27: 6. zmin(1=2; 7=2) = 29=4 7. zmin(3=2; 5=2) = 15=2 8. zmin(¡2; 8) = ¡16,
zmax(2; 8) = 16:

10.1. Метод неопределенных множителей Лагранжа. |
141 |
Выберем множители ¸i i = 1, ... , k так, чтобы выполнялись |
|||||
равенства |
@L |
= 0, ... , |
@L |
= 0: |
|
|
(10.4) |
||||
|
@x1 |
|
|||
|
|
@xk |
|
||
Это всегда можно сделать, т.к. равенства (10.4) приводят к линейной системе уравнений
|
|
|
k |
|
|
|
|
|
|
|
|
@f |
Xj |
@hj |
|
|
|
|
|
||
|
|
+ ¸j |
|
|
= 0, i = 1, ... , k , j = 1, ... , k, |
|
||||
@xi |
=1 |
@xi |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
D(h1, ... , hk) |
|
|
|
|
||
определитель которой |
|
6= 0. Тогда равенство (10.3) |
||||||||
D(x1, ... , xk) |
||||||||||
примет вид |
|
@L |
dxk+1 + ... + |
|
@L |
dxm = 0, |
|
|||
|
|
|
|
(10.5) |
||||||
|
|
@xk+1 |
|
|||||||
|
|
|
|
|
|
@xm |
|
|||
à òàê êàê xk+1, ... , xm являются независимыми, то из (10.5)
имеем |
@L |
= 0, ... , |
@L |
= 0: |
|
@xk+1 |
|
||
|
|
@xm |
||
Дополнив их уравнениями (10.4) получаем утверждение теоремы, т.е. m + k уравнений (10.1) для определения неизвестных
x1, ... , xm, ¸1, ... , ¸k.¤
Достаточные условия условного экстремума проверяются путем определения знака второго дифференциала d2L, íî ïðè ýòîì
следует учесть, что k дифференциалов dx1 ... dxk не являются независимыми, а определяются из системы уравнений (9.17).
Пример 10.1. Требуется определить экстремум функции u =
x + y + z = 4, x ¡ 2y ¡ z = 1.
L= x2 + y2 + z2 + ¸1(x + y + z ¡ 4) + ¸2(x ¡ 2y ¡ z ¡ 1)
èвычислим частные производные
1.@L@x = 2x + ¸1 + ¸2 = 0, 2.@L@y = 2x + ¸1 ¡ 2¸2 = 0,
3.@L@z = 2z + ¸1 ¡ ¸2 = 0, 4.@¸@L1 = x + y + z ¡ 4 = 0,
5. |
@L |
= x ¡ 2y ¡ z ¡ 1 = 0. |
|
|
|||||||
@¸2 |
|
|
|||||||||
Из первых трех уравнений находим |
|
||||||||||
x = |
¡ |
¸1 + ¸2 , |
y = |
2¸2 ¡ ¸1 |
, z = |
¸2 ¡ ¸1 |
: Подставив эти зна- |
||||
|
2 |
|
|
2 |
|||||||
|
|
|
2 |
|
|
||||||
чения в |
последние два уравнения, |
получим 2¸2 ¡ 3¸1 = 8, ¡ |
|||||||||
¡6¸2 + 2¸1 = 2. Решая эту систему уравнений, находим ¸1 = ¡
