
matanaliz
.pdf
52 Лекция 3. Дифференциальное исчисление функции одной переменной
Вычисляя предел отношения lim |
¢y |
|
|
|||||||||
¢x, получим |
|
|||||||||||
|
|
|
|
0 |
|
|||||||
|
|
|
|
|
¢x! |
|
|
|
|
|
|
|
|
¢y |
|
|
¢u |
v(x) ¡ u(x) |
¢v |
|
= |
u0(x)v(x) ¡ u(x)v0(x) |
|
||
lim |
= lim |
|
¢x |
¢x |
:¤ |
|||||||
¢x |
|
|
|
|
|
v2(x) |
||||||
¢x!0 |
¢x!0 |
v(x + ¢x)v(x) |
|
|
|
|
|
|||||
4. Из условий дифференцируемости функций y = f(x) , x = Ã(t) следует
¢y = f0(x)¢x + ®¢x, ¢x = Ã0(t)¢t + ¯¢t,
ãäå ®¢x = o(¢x), ¯¢t = o(¢t) Тогда будем иметь
¢y = f0(x)¢x + ®¢x = f0(x)¢x + ®(Ã0(t)¢t + ¯¢t):
Разделим левую и правую части равенства на ¢t В результате
получим |
|
¢y |
= f0(x) |
¢x |
+ ®Ã0 |
(t) + ®¯: |
||||||
|
|
|
|
|
||||||||
|
|
|
¢t |
|
|
|
|
|
¢t |
|
||
Вычислим предел |
lim |
¢y |
: |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
¢t!0 |
¢t |
|
|
|
|
||||
lim |
¢y |
= f0(x) lim |
¢x |
+ lim (®Ã0 |
(t) + ®¯) = f0(x)Ã0(t):¤ |
|||||||
¢t |
|
¢t |
|
|||||||||
¢t!0 |
|
¢t!0 |
|
|
¢t!0 |
|
||||||
3.1.5. Вычисление производных элементарных функций. Производные тригонометрических функций. y = sin x,
y0 = cosx. Докажем справедливость этой формулы.
|
|
|
|
|
|
|
|
|
lim |
|
¢y |
|
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 ¢x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
¢x! |
|
|
|
|
|
|
|
|
|
|
|||
= lim |
sin(x + ¢x) ¡ sinx |
= |
lim |
|
|
|
2cos(x + ¢x=2)sin(¢x=2) |
= |
|||||||||||||
|
|
|
0 |
|
|
¢x |
|||||||||||||||
¢x! |
0 |
|
|
|
¢x |
|
|
¢x! |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(¢x=2) |
|
|
|
|
||||
|
= |
lim cos(x + ¢x=2) lim |
|
|
= cosx, |
|
|||||||||||||||
|
0 |
¢x=2 |
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
¢x! |
|
|
|
|||||||||
|
|
|
¢x! |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
y = cos x, y0 = ¡sinx |
|
|
|
||||||||||||
|
|
|
|
lim |
¢y |
|
= lim |
cos(x + ¢x) ¡ cosx |
= |
|
|||||||||||
|
|
|
|
¢x |
|
|
|
|
|||||||||||||
|
|
|
¢x!0 |
¢x!0 |
|
|
|
|
|
|
|
¢x |
|
|
|
||||||
|
|
|
|
= lim |
¡2sin(x + ¢x=2)sin(¢x=2) |
= |
|
||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
¢x |
|
|
|
|
|
|||||
|
|
|
|
|
¢x! |
|
|
|
|
|
|
|
|
|
sin(¢x=2) |
|
|
|
|||
= ¡ |
lim sin(x + ¢x=2) lim |
|
|
= sinx, |
|
||||||||||||||||
0 |
¢x=2 |
|
|
||||||||||||||||||
¢x |
! |
0 |
|
|
|
|
¢x |
! |
¡ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = tgx = sinxcosx ,

3.1. Производная, основные понятия и правила дифференцирования 53
y0 = |
sin0xcosx ¡ sinxcos0x |
= |
cos2x + sin2x |
= |
1 |
|
|
cos2x |
cos2x |
cos2x |
|||||
|
|
|
|||||
Аналогичным образом вычисляется производная функции y =
= ctgx,
ctg0x = ¡ 1 : sin2x
Производная логарифмической функции. y = logax, y0 =
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xlna, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
¢y = loga(x + ¢x) ¡ logax = loga ³1 + |
¢x |
´, |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
= |
lim |
|
|
¢y |
|
= |
lim |
|
1 |
log |
|
|
|
1 + |
¢x |
|
= |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
¢x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
(logax) |
¢x!0 |
|
|
¢x!0 ¢x |
|
|
a ³ |
a |
³ |
x |
´ |
|
´ |
|
|||||||||||||||||||||||||
= ¢x!0 x |
a ³ |
|
|
x |
´ |
|
|
|
|
|
|
¢x!0 x ¢x!0 |
|
|
|
|
|
|
x |
|
||||||||||||||||||||||
|
lim |
|
1 |
log |
|
|
|
1 + |
¢x |
|
|
x=¢x |
= |
lim |
|
1 |
|
lim log |
|
|
1 + |
¢x |
|
|
x=¢x = |
|||||||||||||||||
|
|
|
|
|
|
|
|
= ¢x!0 x |
¢ |
|
a ¢x!0 ³ |
|
|
|
|
x |
´ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
log |
|
|
lim |
|
1 + |
¢x |
|
|
x=¢x: |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Воспользуемся вторым замечательным пределом |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
lim |
|
1 |
|
log |
|
lim |
|
|
1 + |
¢x |
´ |
x=¢x |
= 1 |
log |
e = |
|
1 |
|
: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xlna |
|
|||||||||||||||||||||||||||
|
|
¢x!0 x¢ |
|
|
a |
¢x!0 |
³ |
|
|
|
x |
|
|
|
|
|
x¢ |
|
|
a |
|
|
|
|
|
|
||||||||||||||||
Производная обратной функции
Теорема 3.2. Если функция y = f(x) возрастает (убывает)
в некоторой окрестности точки x0 и является дифферен-
цируемой в этой точке, то существует0 обратная0 функция x = '(y),которая имеет производную ' (y0) = 1=f (x0) в точке
y0 = f(x0)
Д о к а з а т е л ь с т в о. Так как функция возрастает (убывает) в некоторой окрестности точки x0, она имеет
обратную функцию. Из условия дифференцируемости следует непрерывность функции. Тогда, если ¢y ! 0, òî ¢x ! 0. Â ýòîì
случае имеем
0 |
|
|
¢x |
|
1 |
0 |
(x0):¤ |
|
||
' |
(y0) = |
lim0 |
|
|
= |
lim0 |
|
= 1=f |
(3.1) |
|
¢y |
¢y=¢x |
|||||||||
|
|
¢y! |
|
¢x! |
|
|
|
|||
Производная показательной функции. |
|||||
Функция y = ax является обратной к фунуции x = lna y. Ïîëü- |
|||||
зуемся формулой (3.1) y0 = |
1 |
|
= |
1 |
= ylna = axlna: |
loga0 |
|
|
|||
|
y |
1=ylna |
|||
Производные обратных тригонометрических функций.

54 Лекция 3. Дифференциальное исчисление функции одной переменной
|
|
|
Функция y = arcsin x, x 2 [¡1; 1] служит обратной для функ- |
||||||||||||||||||||||||||||||||||||||||||||
öèè x = sin y, y 2 h¡2 ; |
|
2 i |
Тогда, (arcsin x) |
|
= (sin y)0 |
= cos y = |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¼ |
|
¼ |
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|||||
= |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
= |
|
|
|
1 |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 ¡ sin2y |
|
|
|
|
1 ¡ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
(arccos x) |
0 |
|
= ¡ |
|||||||||||||||||||||
|
Аналогичным |
образом |
выводится |
формула |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
¡ |
|
|
|
|
|
|
1 |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
производную функции y = arctg x, x 2 (¡1; +1). |
||||||||||||||||||||||||||||||||
|
pВычислим¡ |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ýòà |
|
|
функция является обратной для функции |
x = tg y |
, |
y 2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
¼ |
¼ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
³¡ |
|
|
; |
|
|
´: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
(y = arctg x)0 = |
|
1 |
|
= |
1 |
|
= |
1 |
|
= |
|
|
|
1 |
: |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
(tg y)0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1=cos2x |
|
1 + tg2y |
|
1 + x2 |
|
|
|
|
|
|
|
|||||||||||||||
Аналогичным образом выводится формула (arcctg x) |
0 |
= ¡ |
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
1 + x2 : |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Логарифмическая производная. Если функция y=f(x) ïî- |
||||||||||||||||||||||||||||||||||||||||||||
ложительна и дифференцируема, то справедливы следующие ра- |
||
венства: |
0 |
= y0=y: Величина, определяемая по- |
ln y = ln f(x), (ln f(x)) |
|
|
следней формулой, называется логарифмической производной. Ей удобно пользоваться для вычисления производных от функций вида y = u(x)v(x)
Предполагается, что функции u(x), v(x) являются дифференцируемыми и u(x) > 0 Прологарифмируем равенство y = u(x)v(x).
0
ln y = v(x)ln u(x). Тогда, y0=y = (v(x))0 ln u(x) + v(x)(u(x))
u(x) , откуда получаем y0 = u(x)v(x) µ(v(x))0 ln u(x) + v(x)(u(x))0 ¶:
u(x)
Производная степенной функции y = xa, x > 0:
ln y = aln x =) y0=y = a=x =) y0 = ya=x = axa¡1:
3.2. Понятие дифференциала функции
Определение 3.3. Линейная часть приращения функции относительно ¢x¢y = A¢x + ®¢x называется дифференциа-
лом функции |
dy = A¢x: |
|
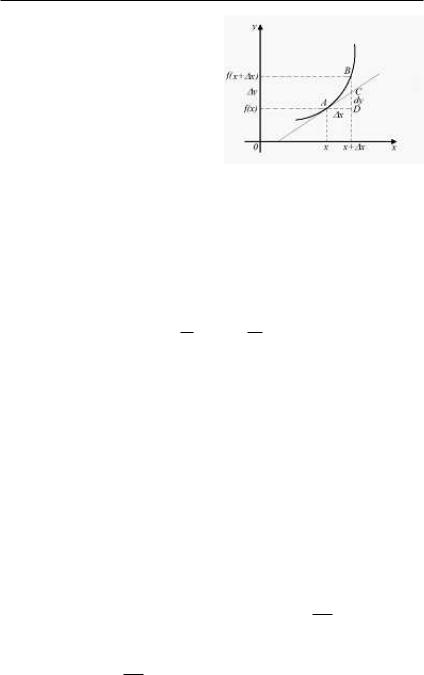
3.3. Производные и дифференциалы высших порядков |
55 |
Геометрическая интерпретация дифференциала приведена на рис. 3.2. Из треугольника ACD имеем
dy = f0(x)¢x Отрезок
CD = dy, BD = ¢y, BC =
=®¢x
Âкачестве дифференциала независимой переменной x áó-
дем брать число равное приращению ¢x, dx = ¢x Тогда
формулу для дифференциала функции можно записать в виде
Ðèñ. 3.2.
dy = f0(x)dx:
Инвариантность формы первого дифференциала. Покажем, что приведенная формула является справедливой и для сложной функции.
y = f(Ã(t)), ãäå x = Ã(t). В соответствии с правилом дифференцирования сложной функции имеем y0 = f0(x)Ã0(t) Запишем
эту формулу в другом виде dydt = f0(x)dxdt . Умножив это равенство íà dt, получим
dy = f0(x)dx Таким образом, независимо от того какой яв-
ляется функция сложной или простой, дифференциал ее равен произведению производной на дифференциал аргумента. Другими словами форма дифференциала не зависит от того, каким является аргумент зависимой или независимой переменной.
3.3. Производные и дифференциалы высших порядков
Пусть задана функция y = f(x), x 2 (a; b), которая имеет дифференцируемую производную y0 = f0(x) в точке
Если производная f0(x) является дифференцируемой функцией, то можно вычислить ее производную ¡y0¢0 = ¡f0(x)¢0. Ýòà ïðî- изводная является второй производной для функции y = f(x),
которая имеет следующие обозначения: y00, yÄ, d2y
dx2 . Если вторая
производная является дифференцируемой функцией, то можно вычислить производнуюµ ¶ этой функции, которая будет третьей производной y000 d3y , для исходной функции y = f(x) Ïî-
dx3

56 Лекция 3. Дифференциальное исчисление функции одной переменной
вторяя эти процедуры, при условии, что полученные производные являются дифференцируемыми функциями, можно получить производные любого порядка. Условно будем пользоваться следующими обозначениями для производной n-ого порядка y(n) èëè
dny dxn :
|
Пример |
|
3.1. |
|
|
y = |
|
ln(x2 |
+ 1). |
Вычислим производ- |
||||||||||||||||||
íóþ |
y0 |
|
= |
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y00 |
= |
|||
|
|
x2 + 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
|
|
¡ |
|
|
|
|
¡ |
Вычислим |
|
|
вторую |
|
производную |
|
|||||||||||||
2 |
0 |
|
2 |
x2¢+ 1 |
|
|
|
|
¢ |
0 |
= |
|
|
|
|
|
|
|
|
|
|
|||||||
|
( x) |
|
|
x |
|
+ |
|
¡ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
¢ |
|
|
2(x |
2 |
+ |
1 |
4 |
x |
2 |
|
|
2 |
x |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
= |
|
|
|
) ¡2 |
|
= |
2 ¡ |
|
|
2 |
: |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡x2 + 1¢ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
¡x2 + 1¢ |
|
|
|
|
|
|
|||||||||
Определение 3.4. Дифференциал от дифференциала
d (dy) = d (df(x)) функции y = f(x) называется дифференциалом второго порядка и обозначается d2y
Найдем формулу для вычисления дифференциала второго прядка ³ ´ ³ ´
d2y = d f0(x)dx = d f0(x) dx + f0(x)d (dx) =
Принимая во внимание то, что x является независимой переменной, получаем равенство d (dx) = 0. В результате имеем
³ ´
d2y = d f0(x) dx = f00(x)dx2=
Аналогичным образом получается формула для дифференциала n-ого порядка
Следует отметить, что дифференциалы высших порядков не обладают свойством инвариантности. Иными словами, если переменная x не является независимой, то формула для вычисления
принимает другой вид.
Для дифференциала второго порядка имеем
d2y = f00(x)dx2 + f0(x)d2x:
3.4. Производные функций, заданных в параметрической форме
Пусть функция y îò x задана в параметрической форме
3.4. Производные функций, заданных в параметрической форме |
57 |
y = Ã(t), x = '(t), t 2 [t0; T ]: Предположим, что эти функции дифференцируемы в точке t 2 [t0; T ], '0(t) 6= 0, функция '(t)
в окрестности точки t имеет обратную функцию t = ©(x): Òðå-
буется найти формулу для вычисления производной dxdy . Будем рассматривать функцию
y = Ã(t) как сложную функцию y = Ã(©(x)). Используя
правило дифференцирования сложной функции, получим dxdy = |
|
= Ã0©0 |
|
t x. Здесь индекс указывает по какой переменной осуществ- |
|
ляется дифференцирование. |
|
Воспользуемся правилом вычисления производной для об- |
|
ратной функции (теорема3.2) ©x0 = 10 . В результате получаем |
|
формулу |
't |
dy |
= Ãt0 : |
dx |
't0 |
Будем считать,0 что в параметрической форме задана функция dy = Ãt0 = Â(t), x = '(t) : Тогда, пользуясь полученной фор-
dx 't
мулой для первой производной, получим формулу для вычисления второй производной
d2y = Â0t = dx t : dx2 '0t '0t
Аналогичным образом получаем формулу для вычисления производной любого порядка, предполагая, что они существуют и выполнены предположения, сделанные вначале
µdn¡1y ¶0
|
|
|
|
dny |
= |
|
dxn¡1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
t |
: |
|
|
||||
|
|
|
dx |
n |
|
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
't |
|
|||||||||
|
y = cos t, |
|
|
|
|
dy |
|
|
|
sin t |
|
||||||
Пример 3.2 |
½ x = sin t: |
|
=) |
|
|
= ¡ |
|
|
= ¡tgt , =) |
||||||||
|
dx |
cos t |
|||||||||||||||
|
|
d2y |
|
|
((¡tg t))t0 |
1 |
|
|
|||||||||
|
|
dx2 |
= |
|
cos t |
|
|
|
= ¡ |
cos3t |
|
: |
|||||
3.4.1. Контрольные вопросы. 1. Сформулируйте определение производной и поясните ее геометрический и физический смысл.

58Лекция 3. Дифференциальное исчисление функции одной переменной
2.Выведите правила дифференцирования.
3.Выведите формулы дифференцирования для элементарных функций.
4.Что такое дифференциал функции и его геометрический смысл?
5.В чем состоит инвариантность первого дифференциала?
6.Выведите формулы для вычисления производных для функций, заданных в параметрической форме.
3.5. Методические указания по решению задач
Для вычисления производных пользуемся правилами дифференцирования и таблицей производных
Таблица производных основных элементарных функций.
|
1. |
(xm)0 = mxm¡1, |
|
10. |
(arcsin x)0 = |
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2. |
(ex)0 |
= ex, |
|
|
|
|
|
11. |
(arccos x)0 |
= p |
¡ |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 ¡ x2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
3. |
(ax)0 |
= ax ln a, |
|
|
|
12. |
(àrctgx)0 = |
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
1 + x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
4. |
|
|
|
0 |
1 |
|
|
|
|
|
|
àrcctg |
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
(ln x) = x, |
|
1 |
|
|
|
13.( |
|
|
|
x) = ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
5. |
(lna x)0 = |
|
|
, |
|
14. |
(shx)0 = µ |
ex ¡ e¡x |
¶0 |
|
= chx, |
|
|
|
|||||||||||||||||||||||||||||||
|
|
x ln a |
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
6. |
(sin x)0 |
= cos x, |
´ |
|
15. |
(chx)0 = µshx |
20 |
¡ |
|
|
¶ |
|
|
|
|
= shx, |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
³ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex + e |
|
x |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
7. (cos x)0 |
= |
¡ |
sin x, |
|
16. |
(thx)0 = |
³ |
chx´ |
= |
|
1 |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
chx |
|
|
|
|
|
ch2 , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
8. |
(tgx)0 = sec2x, |
|
|
|
17. (cthx)0 = ³ |
|
|
´0 |
|
= ¡ |
1 |
, |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
shx |
|
sh2x |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
9. |
(ctgx)0 = ¡cosec2x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1. Найти производную функции y = µ |
2 x21+ x4 |
¶: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной частного: Воспользуемся правилами |
|
p |
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Решение: |
|
|
|
|
|
2 µ |
|
|
|
p |
|
|
|
нахождения производ- |
||||||||||||||||||||||||||||||||
y0 = µ2 1 x4 ¶ |
0 |
= |
(x2 + 2)0 |
¡( 1¡ x4 )2 |
|
|
|
p |
|
|
¡ |
|
|
)0 |
¶ |
= |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
x2 + 2 |
|
|
1 |
|
1 |
x4 |
|
|
(x2 + 2)( 1 |
|
|
x4 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
p ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
p ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

|
|
|
|
3.5. Методические указания по решению задач |
|
|
|
|
|
|
|
59 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
¡ ¡ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 ¡ |
x4 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
2 |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 ¡ x4)p |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
B |
2x 1 x4 |
|
|
|
|
|
|
(x2 + 2) (¡4x3) |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
@ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
x(1 ¡ x4) + x3(x2 + 2) |
|
|
= |
x ¡ x5 + x5 + 2x3 |
|
|
|
|
|
= |
|
|
|
2x3 + x |
: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
(1 ¡ x4)p1 ¡ x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(1 ¡ x4)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(1 ¡ x4)3 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||||||||||||
2. Найти |
|
производную |
|
функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
¡ |
1 |
|
||||||||||||||||||||||||||||||||||||||||||||||
+ arcsine¡x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ln (e |
|
|
+ e |
|
) + |
|||||||||||||||||||||||||||||||||||||
Решение: Воспользуемся правилами нахождения производ- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ной суммы и производной сложной функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y0 = (ln(ex + p |
|
|
|
|
|
|
|
|
|
|
|
))0 + (arcsin e¡x)0 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
e2x |
¡ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex + |
|
|
|
(e2 |
x ¡ 1)0 |
|
|
|
|
|
|
||||||||||||||||||||||
= |
|
|
ex +pe2x ¡ 1 |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 e¡2x = ex + |
|
2pe2x ¡ |
1 + |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(ex + e2x |
|
|
|
1 )0 |
|
|
|
|
|
|
|
|
|
|
|
(e¡x)0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2x |
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
¡ ex + |
|
|
|
p2e¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
+ |
|
|
1¡ e |
|
|
|
|
= ex |
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
¡ |
|
|
|
1 e 2x |
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
2x |
+ 2pe2x |
|
|
¡1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
( e¡x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
e¡x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
= |
p |
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
+ p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
¡ x |
|
|
|
2x |
|
|
|
1 |
|
|
|
|
e |
2x |
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x |
e2x |
¡ |
1 ) |
|
¢ p |
å2x |
¡ |
1 |
|
exse |
2x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2¡x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
(e + |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
(e |
|
+ |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
= |
|
|
|
|
ex( e2x ¡ 1 + ex) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
e2x |
¡ |
1 ) |
|
¢ p |
|
|
|
2x |
¡ |
1 ¡ |
|
p |
2x |
|
¡ |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
= |
ex ¡ 1 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex ¡ 1 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
ex ¡ 1 |
|
: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rex + 1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
pe2x ¡ 1 |
|
|
pex ¡ 1 ¢ pex + 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Найти производную: y = ln r4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1 ¡ 2x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение: При дифференцировании некоторых логарифмиче- |
|||||||||||||
ских выражений рациональнее предварительно упростить перво- |
|||||||||||||
начальную функцию по свойствам логарифма: |
|
|
|
|
|
||||||||
4 |
1 + 2x |
1 1 |
+ 2x |
1 |
1 |
|
2 |
x) ¡ ln( |
1 |
¡ |
2 |
|
; |
y = ln r |
1 ¡ 2x |
= 4 ln 1 |
¡ 2x = |
4 (ln( |
|
+ |
|
|
|
x)) |
|
||

60 |
Лекция 3. |
|
|
Дифференциальное исчисление функции одной переменной |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
= 1(ln(1 + 2x))0 |
|
|
|
(ln(1 |
|
|
|
|
|
|
|
2x))0) = 1 |
|
µ |
(1 + 2x)0 |
|
|
(1 ¡ 2x)0 |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
¡ |
|
¡ |
|
|
|
|
1 + 2x |
¡ |
1 ¡ 2x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
¶ |
|
|||||||||||||||||||||||||||||||||||||||||
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡2 |
|
|
´ |
|
= 1 |
|
³ |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
1 |
|
|
|
|
´ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
1 + 2x ¡ |
|
|
|
|
|
|
|
|
|
|
|
1 + 2x |
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
1 |
2 |
|
2x |
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(³1 |
¡ |
2x + 1 +¡x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
= 1 |
|
|
|
|
1 ¡ 4x2 |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
1 |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ¡ 4x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
4. Найти производную: |
|
y = |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
¡ x |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ x ¡ x ¢ arcsin |
|
|
|
|
|
|
|
: |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x2 ) |
0 ¡ |
(x |
¢ |
arcsin |
|
p |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 = (p(1 |
|
¡x2)0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ x )0 = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x arcsin |
|
|
|
1 |
|
|
|
|
x2 + |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2p1 ¡ |
x2 |
|
|
|
¡ |
|
|
|
|
|
0 |
|
|
|
2x |
|
p |
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
+x |
¢ |
(arcsin |
|
1 |
¡ |
x2 ) ) = |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
(arcsin |
1 |
¡ |
x2 + |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 ¡ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
)0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
+x |
|
|
|
|
|
(p |
|
|
¡ x |
|
|
|
|
|
|
|
) = ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ arcsin |
|
|
1 ¡ x2 ¡ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
q1 ¡ ( 1 ¡ x2 )2 |
|
|
|
|
|
|
|
|
|
|
|
p |
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(p2x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ arcsin p1 ¡ x2 + |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
¡x |
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
1 |
+ x |
2 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2px2¡ x |
|
|
|
¢ |
=p ¡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pjxj¡ |
|
x |
|
|
|
arcsin p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
1 |
¡ |
x2 : |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
jxj |
|
1 |
¡ x |
2 |
|
|
|
|
|
¡ |
|
|
|
1 |
|
¡ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
¡ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. Найти производную: y = (tgx) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение: |
|
|
Прологарифмируем |
|
|
|
выражение: y = (tgx)ln tgx4 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ln y = ln(tgx)ln tgx4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
Упростим правую часть по свойству логарифмической функ- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
öèè: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln y = ln tg |
x |
¢ ln tgx: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Продифференцируем левую и правую части этого равенства, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
учитывая, что y |
|
функция от x, à lny |
|
сложная функция: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y0 |
|
= |
|
³ln tg |
x |
´0 |
ln tgx + ln tg |
x |
¢ (ln tgx)0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
1 sec2 |
x |
|
ln tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
sec2 x |
|
|
|
|
|
|
|
|
|
|
ln tgx |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ln tg |
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
tgx |
|
|
|
4 |
|
|
|
|
|
x |
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
4 ¢ sin |
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln tg |
x |
|
|
|
|
|
= |
ln tgx |
|
|
|
|
2 ln tg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
4 |
|
|
|
|
+ |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
sin |
|
x |
|
|
|
|
|
|
sin 2x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

y0 = |
à |
3.5. Методические указания по решению задач |
! |
|||||||||||||
2 sin x2 |
+ sin 2x4 |
! y; |
y0 = |
à |
2 sin x2 |
+ sin 2x4 |
||||||||||
|
|
ln tgx |
|
2 ln tg |
x |
|
|
|
ln tgx |
2 ln tg |
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61
ln tgx
(tgx) 4 :
6. Найти производную: y = xesin x :
Решение: Данная функция показательно - степенная. Проло- гарифмируем все выражение: ln y = ln xesin x . По свойству лога-
ln y = esin x ln x. Продифференци-
руем все выражение, учитывая, что y функция от x, à lny сложная функция:
|
y0 |
= |
esin x |
|
, ln x + esin x(ln x)0 |
; y0 |
= esin x cos x |
ln x + |
esin x |
|
|
|
|||||
|
|
|
|
|
|
|
e;sin x |
|
|||||||||
y0 = e |
|
³cos x ¢ ln x + x´ y ; |
y0 = e |
|
³cos x ¢ ln x + x |
´ x |
: |
||||||||||
|
y |
sin |
¡x |
¢ |
1 |
|
y |
|
sin x |
¢ |
1 |
x |
|
||||
7.Найти производную от параметричåской функции:
½x = arcsin pt y = p pt :1 +
Решение: Воспользуемся правилом0 дифференцирования параметрической функции: yx0 = yt0 :
xt
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
+ |
|
t |
)0 |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
yt0 = (p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
+ pt )0 = |
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4pt |
|
|
1 + pt |
; |
||||||||||||||||||||||||||||||||||||||||||||||||
|
2 1 + pt |
|
|
|
|
|
1 + pt |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x0 |
= (arcsin |
|
t ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 ¡ (p |
|
|
)2 |
|
|
|
|
|
|
2pt p1 ¡ t ; |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
2p |
|
p |
|
|
|
|
|
= |
q |
|
|
|
|
q |
|
|
|
|
|
|
= |
q |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
yt0 |
|
|
|
|
|
|
|
|
1 ¡ p |
|
|
1 + p |
|
1 ¡ p |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
t |
t |
t |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
yx0 = |
|
t |
1 ¡ t |
|
: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
4p |
|
|
q1 + p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
xt0 |
|
|
|
|
|
|
|
|
|
|
2q1 + p |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
t |
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
8. Составить уравнение нормали и уравнение касательной к |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
кривой y = x + px3 в точке с абсциссой x0 |
=1. |
|
|
|
|
|
||||||||||||||||||
|
Решение: Уравнение касательной к кривой ó=f(x) в точке |
|||||||||||||||||||||||
M0 |
(x0, y0) имеет вид: y |
¡ |
y0 = y0 |
(x |
¡ |
x0). |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
Уравнение нормали имеет вид: |
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
.Найдем |
|||||||||
|
y ¡ y0 = ¡y00 |
|
|
) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x ¡ x |
|
||||||||||||
производную функции в точке с абсциссой x0 =1. |
|
|
|
|
||||||||||||||||||||
|
y0 = (x + p |
|
)0 = 1 + 2px |
|
|
y0 ( |
|
) = |
|
+ |
2p |
|
= |
|
||||||||||
|
x3 |
|
|
|
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
; |
|
|
|
1 |
|
|
1 |
|
|
3 |
1 |
|
|
5 ; |
