
matanaliz
.pdf

234 |
Лекция 16. Несобственные интегралы |
с неотрицательными, неограниченными функциями f(x) è g(x)
справедливы теоремы сравнения, аналогичные теоремам 16.1 и 16.2. Отличие состоит в том, что полуинтервал [a, 1) заменяется
на полуинтервал [a, b),в случае, если особые точки функций
находятся в точке x = b. Соответственно изменяются эти полу-
интервалы и в случаях, когда особые точки находятся слева или в самом интерале (a, b)
Пример 16.6. Исследовать на сходимость интеграл
Z¼
2 + sinxdx:
(¼ ¡ x)2
0
Подынтегральная функция имеет особую точку x = ¼. На отрезке [0, ¼] функция sinx > 0. Возьмем для сравнения интеграл
¼ |
¡ |
|
|
¼¡" |
¡ |
|
³ |
1 |
|
|
´ |
|
0 |
|
|
0 |
|
|
|
|
|
||||
Z |
1 |
|
lim |
Z |
1 |
dx = lim |
|
|
|
|
1 |
|
(¼ x)2 dx = |
(¼ x)2 |
|
" ¡ |
= 1: |
||||||||
"!0 |
"!0 |
|
¼ |
|||||||||
Òàê êàê |
2 + sinx |
> |
1 |
|
|
|
(¼ ¡ x)2 , |
||
|
(¼ ¡ x)2 |
|||
то исследуемый интеграл расходится.
16.5.Контрольные вопросы
1.Как определяется несобственный интеграл с бесконечными пределами?
2.Сформулируйте правило вычисления несобственных интегралов первого рода.
3.Сформулируйте первую и вторую теорему сравнения для несобственных интегралов первого рода.
4.Какой несобственный интеграл второго рода называется абсолютно сходящимся, и какой условно сходящимся?
5.Сформулируйте определение несобственного интеграла от неограниченных функций.
6.Сформулируйте первую и вторую теорему сравнения для несобственных интегралов второго рода.
7.. Сформулируйте правило вычисления несобственных интегралов второг рода.



16.7. Примеры для самостоятельного решения |
237 |
Интеграл 1R1 cosxx2 dx сходится. Таким образом получили, что исходный интеграл абсолютно не сходится, хотя сам является сходящим. Иными словами имеем условную сходимость.
16.7. Примеры для самостоятельного решения
Вычислить несобственные интегралы (или установить их расходимость)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
1 arctgxdx |
|
1 2xdx |
|||||||||||||||||||||||||
1. ¡1 x2 + 4x + 9. |
2. 0 |
|
|
x2 + 1 . |
3. ¡1 x2 + 1. |
|||||||||||||||||||||||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 ln xdx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
4.. R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
R0 |
xe¡x2 dx. |
6. R0 |
x sin xdx. |
||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
dx |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
7. |
e¡px dx. |
|
|
|
|
|
|
8. x3e¡x2 dx. |
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
x2(x + 1). |
|||||||||||||||||||||||||||||||||||||
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
xdx |
|
|
|
|
|
|
|
|
|
1/2 |
|
dx |
|
|
|
|
¼/2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10. 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgxdx. |
||||||||
|
|
(1 + x)3 . |
|
|
11. |
0 |
|
|
x ln x. |
12. |
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
||||||||||||
13. |
2 |
|
xdx |
|
|
|
|
|
|
|
|
|
|
|
e |
|
dx |
|
|
|
|
|
|
|
3 |
|
|
dx |
||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
xp |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
(x |
|
|
|
1)2 . |
||||||||||||||||||||||
|
x |
|
|
|
1 . |
|
|
|
|
|
|
14. |
ln x |
15. |
|
|
|
|
||||||||||||||||||||||||||
|
R |
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
|
R6 |
|
|
|
|
|
|
|
|
|
R1 |
|
|
|
¡ |
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||
16. |
|
|
|
|
|
|
xdx |
|
|
|
. |
|
17. |
|
|
|
|
|
|
|
|
|
ln xdx. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
7x + 10. |
18. |
|
|
|||||||||||||||||||||||
0,5 |
1 |
|
|
|
x |
2 |
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1R |
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
|
R32 |
¡ |
|
|
|
|
|
|
R27 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
arcsin xdx |
|
|
|
|
|
|
|
4x3dx |
|
|
|
|
|
dx |
|
|
|
|
|||||||||||||||||||||||
19. |
R0 |
|
p |
|
|
|
|
|
|
|
|
|
|
. |
|
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
1. |
|
21. |
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
|
x2 |
|
2 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
px . |
||||||||||||||||||||||||||||||
|
|
|
¡ |
|
|
|
|
|
|
|
|
|
¡R |
|
|
¡ |
|
|
|
|
|
¡R |
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
3 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
22. |
¡R1 |
px |
|
|
+ |
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
px2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
16.7.1. Ответы. 1. ¼±p5 . 2. ¼2/8. 3. Расходится. 4.
Расходится. 5. 1/2. 6. Расходится. 7. 2. 8. 1/2. 9. 1 ln2. 10. 1/2. 11. Расходитсяp ± . 12. Расходится. 13. 8/3. 14. 2. 15. Расходит-
ся. 16. 3 2. 17. Расходится. 18. 1.
19. ¼2/8. 20. Расходится. 21. 15/2. 22. 144. 7
Ë å ê ö è ÿ 17
ДВОЙНЫЕ ИНТЕГРАЛЫ
17.1. Определение и существование двойного интеграла
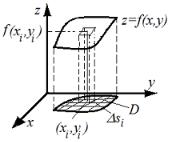
Пусть в области D задана непрерывная функция z = f(x, y). Разобьем область D íà n частных участ-
ков. Обозначим |
данное разбиение |
|
символом Tn. Обозначим символом |
||
¢si |
площадь i-й частной подобла- |
|
сти, и выберем произвольно точки |
||
с координатами (xi, yi), и составим |
||
интегральную сумму |
||
|
n |
|
|
Xi |
|
Ðèñ. 17.1. |
JT (f) = |
f(xi, yi)¢si: |
|
=1 |
|
Определение 17.1. Число JT (f) называется интегральной суммой, соответствующей данному разбиению Tn и данному вы- бору точек (xi, yi)
Обозначим через ¢ максимальную площадь имеющихся под-
областей ¢si
¢ = maxf¢s1, ¢¢¢ , ¢sng:
Очевидно, что каждое слагаемое f(xiyi)¢si в интегральной сум- ме численно равняется объему криволинейного параллелепипеда с площадью основания ¢si и высотой f(xiyi)
Определение 17.2. Функция z = f(x, y) называется интегрируемой по Риману в области D, если существует число I,
такое что для любого разбиения Tn (xi, yi) 2 ¢si выполняется равенство
|
n |
|
|
Xi |
|
lim |
f(xi, yi)¢si = I: |
(17.1) |
4!0 |
=1 |
|

240 |
Лекция 17. Двойные интегралы |
Теорема 17.1. Для того чтобы ограниченная в области D
функция f(x, y) была интегрируема необходимо и достаточ- но, чтобы выполнялось условие
lim0 |
(ST ¡ sT ) = 0: |
(17.3) |
4! |
|
функция f(x, y) |
Теорема 17.2. Непрерывная в области D |
||
интегрируема на этой области. |
|
|
17.2. Основные свойства двойного интеграла
Свойства двойного интеграла аналогичны свойствам обычного определенного интеграла. Поэтому приведем их без доказательства.
1. Линейное свойство. Если функции f(x, y), g(x, y) интегрируемы в области D, то функция ®f(x, y) § ¯g(x, y) , ãäå ®, ¯ -
некоторые вещественные числа. При этом справедливо равенство
ZZ ZZ ZZ
(®f(x, y) § ¯g(x, y)) ds = ® f(x, y)ds § ¯ g(x, y)ds:
D D D
2. Если функция f(x, y) интегрируема в области D, а область D
разбита непрерывной кривой на две D1 è D2, то функция f(x, y) |
|||
интегрируема в каждой из областей и справедлива формула |
|||
ZZ |
f(x, y)ds = ZZ1 |
f(x, y)ds + ZZ2 |
f(x, y)ds: |
D |
D |
D |
|
3. Если функции f(x, y), g(x, y) интегрируемы в области D, то их произведение тоже интегрируемо в области D:
4. Если функции f(x, y), g(x, y) интегрируемы в области D,
и выполнено неравенство
f(x, y) 6 g(x, y), то справедлива оценка
ZZ ZZ
f(x, y)ds 6 g(x, y)ds:
DD
5.Если функция f(x, y) интегрируема в области D, то функция
jf(x, y)j тоже интегрируема в области D и справедлива оценка
¯ |
|
f(x, y)ds¯ |
6 |
ZZ |
j |
f(x, y) |
j |
ds: |
¯ZZ |
¯ |
|
|
|
||||
¯ |
D |
¯ |
|
D |
|
|
|
|
¯ |
|
¯ |
|
|
|
|
|
|
¯ |
|
¯ |
|
|
|
|
|
|
¯ |
|
¯ |
|
|
|
|
|
|

17.3. Сведение двойного интеграла к повторному однократному 241
6. Теорема о среднем. Если функции f(x, y), g(x, y) интегрируемы в области D è g(x, y) > 0, то существует число ¹, удовлетворяющее неравенству m 6 ¹ 6 M, ãäå
M = sup f(x, y), m = inf f(x, y)
x,y2D x,y2D
такое, что справедлива формула |
||
|
ZZ f(x, y)g(x, y)ds = ¹ ZZ g(x, y)ds: |
|
|
D |
D |
При этом найдется точка (», µ) 2 D такая, что будет иметь место |
||
равенство |
ZZ f(x, y)g(x, y)ds = f (», µ) ZZ g(x, y)ds: |
|
|
D |
D |
Åñëè g(x, y) = 1, то получим частный случай |
||
ZZ |
f(x, y)ds = ¹SD |
ZZ f(x, y)ds = f (», µ)SD , |
D |
|
D |
ãäå SD площадь области D:
17.3. Сведение двойного интеграла к повторному однократному
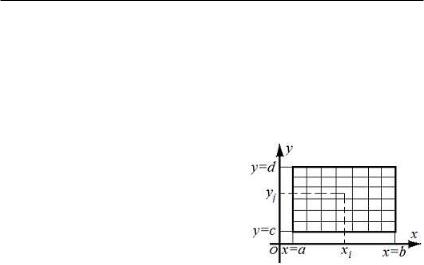
Теорема 17.3. Предположим, что для функции f(x, y)
в прямоугольнике (ðèñ.17.2) существует двойной интеграл. Пусть для любого x 2 [a, b] существует интеграл
Zd
I(x) = f(x, y)dy:
c
Тогда существует повторный интеграл
I = |
Za |
I(x)dx = |
Za |
dx Zc f(x, y)dy: |
|
b |
|
b |
d |
Д о к а з а т е л ь с т в о. Разобьем прямоугольник точками
a = x0 < x1 < ¢¢¢ < xn = b, c = y0 < y1 < ¢¢¢ < ym = d. В каждом
частном прямоугольнике справедливы неравенства
mij 6 f(x, y) 6 Mij, |
(17.4) |
