
matanaliz
.pdf
262 Лекция 18. Тройные и криволинейные интегралы
Для определения статических моментов относительно координат- |
||||||||||
ных плоскостей используются формулы: |
|
|
|
|||||||
Myz = ZZZ |
x¹(x, y, z)dxdydz, Mzx = ZZZ y¹(x, y, z)dxdydz, |
|||||||||
V |
|
|
|
|
|
|
V |
|
|
|
|
Mxy = ZZZ z¹(x, y, z)dxdydz: |
|||||||||
|
|
V |
|
|
|
|
|
|
|
|
Формулы для вычисления центра тяжести имеют вид |
||||||||||
|
x¤ = |
Myz |
|
y¤ = |
Mzx |
|
z¤ |
= |
Mxy |
: |
|
|
m , |
|
m , |
|
|
m |
|||
Кинетические моменты инерции относительно осей координат можно вычислить, используя следующие формулы:
Jx = ZZZ ¡y2 + z2¢¹(x, y, z)dxdydz, Jy = ZZZ ¡x2 + z2¢¹(x, y, z)dxdydz,
V V
Jz = ZZZ ¡y2 + x2¢¹(x, y, z)dxdydz:
V
18.2. Криволинейные интегралы
Пусть на плоскости задана кривая L,
не имеющая точек пересечения и самоналегания, рис. 18.4, кривая AB
Предположим, что кривая определяется в параметрической форме с помощью уравнений: x = '(t), y = Ã(t),
t 2 [a, b]: Будем считать, что вдоль
этой кривой определены и непрерывны Ðèñ. 18.4. функции: f(x, y), P (x, y), Q(x, y): Разобьем êðèвую произвольным образом на n
участков точками Это разбиение обозначим сим-
волом Tn. На каждом учàñòêе возьмем произвольные точки с
координатами (xi, yi), i = 0, n каждой из которых соответствует параметр
n |
n |
|
Xi |
X |
|
J1(f) = f(xi, yi)¢li, J2(P ) = |
P (xi, yi)¢xi, |
(18.1) |
=1 |
i=1 |
|
18.2. Криволинейные интегралы |
263 |
||
|
n |
|
|
|
J2(Q) = XQ(xi, yi)¢y: |
|
|
|
i=1 |
|
|
Определение 18.2. Если существуют конечные пределы |
|
||
lim |
J1(f), lim J2(P ), |
lim J2(Q): |
(18.2) |
4l!0 |
4l!0 |
4l!0 |
|
ãäå ¢l = maxf¢l1, ¢¢¢ , ¢lng, независящие от способа раз-
биения Tn и выбора точек с координатами (xi, yi), то эти пределы называются криволинейными интегралами и обозна- чаются Z
1: lim J1(f) = f(x, y)dl:
4l!0
|
|
|
Z |
L |
Z |
|
: |
4l!0 |
4l!0 |
||
2 |
|
lim |
J2(P ) = |
P (x, y)dx , 3: lim J2(Q) = |
Q(x, y)dy: |
|
|
|
L |
|
L |
Первый интеграл называют криволинейным интегралом первого |
||
рода. Второй и третий называют криволинейными интегралами |
||
второго рода. Сумму |
Z P (x, y)dx + Q(x, y)dy |
|
Z |
P (x, y)dx + Z Q(x, y)dy = |
|
L |
L |
L |
называют общим криволинейным интегралом второго рода. Анализируя интегральные суммы, можно сделать вывод о
том, что криволинейный интеграл первого рода не зависит от направления интегрирования. Интегралы второго рода при изменении направления интегрирования меняют знак на противоположный. Это связано с тем что переменные ¢xi, ¢yi изменяют знак при изменении направления интегрирования.
Особо следует оговорить случай, когда кривая L является за-
мкнутой. Из двух возможных направлений обхода будем считать положительным то направление, когда при обходе контура область ограниченная этим контуром остается слева по отношению к точке обхода. Другими словами, обход против часовой стрелки будем считать обходом в положительном направлении. Интеграл по замкнутому контуру, часто обозначают следующим символом
I
P (x, y)dx + Q(x, y)dy:
L

264 |
Лекция 18. Тройные и криволинейные интегралы |
18.2.1. Способы вычисления криволинейных интегралов. Пусть уравнение кривой L, y = ´(x) является диф-
ференцируемым. Тогда вычисление криволинейных интегралов осуществляется путем преобразования их в обычные определенные интегралы. Подставим значение y = ´(x) в криволиней-
ныq интегралq первого рода, принимая во внимание равенство dl = 1 + (´0(x))2 dx. В результате подынтегральная функция будет зависеть только от переменной x. Если эта переменная
при обходе кривой L изменяется в пределах сегмента [a, b], то в результате получим
Z f(x, y)dl = |
Zb f(x, ´(x))q |
|
dx: |
|
1 + (´0(x))2 |
(18.3) |
|||
L |
a |
|
||
Выполним подстановку y = ´(x) в криволинейный интеграл второго рода, принимая во внимание равенство dy = ´0(x)dx
Z |
P (x, y)dx + Q(x, y)dy = Zb (P (x, ´(x) ) + Q(x´(x))´0(x))dx: |
|
L |
a |
(18.4) |
|
|
|
|
Если уравнение кривой задано в параметрической форме x = |
|
= '(t), y = Ã(t), t 2 [®, ¯], то осуществив замену переменных получим
Z Z¯ q
f(x, y)dl = f('(t), Ã(t)) ('0(t)))2 + (Ã0(t)))2 dt:
LZ®
P (x, y)dx + Q(x, y)dy =
L
Z¯ ³ ´
= P ('(t), Ã(t))'0(t) + Q('(t), Ã(t))Ã0(t) dt:
®
Таким образом, получены формулы преобразования криволинейных интегралов в определенные интегралы. При этом интегрирование ведется по переменной x если пользоваться фор-
мулами (18.3) и (18.4). Следует отметить, что интегрирование можно осуществлять и по переменной y: Выбор остается за
пользователем.

18.2. Криволинейные интегралы |
265 |
Следует отметить, что криволинейные интегралы обладают теми же свойствами, что и обычные определенные. Их не трудно доказать, используя методику доказательств свойств определенного интеграла. Поэтому перечислим основные из них без обоснования их справедливости.
1.ZЕсли существуют интегралыZот функций f(Zxy), g(x, y), òî
(®f(x, y) § ¯g(x, y)) dl = ® |
f(x, y)dl § ¯ |
g(x, y)dl: |
L |
L |
L |
ãäå ® è ¯ любые постоянные.
2. Если существуют интеграл от функции f(xy), а кривая L
состоит из двух кусочно-гладких кривых L1, L2 òî |
||||
Z f(x, y)dl = |
Z1 |
f(x, y)dl + |
Z2 |
f(x, y)dl: |
L |
L |
|
L |
|
3. Если существуют интеграл от функции f(xy)по кривой L, òî
существует интеграл от функции jf(x, y)j, и справедлива оценка |
||||||
¯ |
f(x, y)dl¯ |
6 |
Z j |
f(x, y) |
|
dl: |
¯Z |
¯ |
|
|
j |
|
|
¯L |
¯ |
|
L |
|
|
|
¯ |
¯ |
|
|
|
|
|
¯ |
¯ |
|
|
|
|
|
¯ |
¯ |
|
|
|
|
|
4. Формула среднего значения. Если функция f(xy) непрерывна
вдоль кривой L, то на этой кривой существует точка M(x¤, y¤) такая, что справедливо равенство
Z
f(x, y)dl = lf(x¤, y¤),
L
ãäå l - длина кривой.
В случае, когда рассматривается трехмерное пространство и кривая L является пространственной кривой, то криволинейный
интеграл второго рода имеют вид
Z
P (x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz:
L
18.2.2. Связь между криволинейными интегралами первого и второго рода. Обозначим через ® è ¯ углы, которая
составляет касательная с осями координат в точке A íà ðèñ. 18.5
Тогда получим |
dx = cos®dl, dy = cos¯dl: |
|


268 Лекция 18. Тройные и криволинейные интегралы
Расставим пределы интегрирования в |
|
|
|
|
|
|
|
|
|
||||||||||||||||
повторном интеграле и вычислим его: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
3x |
xy |
|
|
|
|
2 |
3x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Z x2dx Z dy |
Z |
zdz = Z x2dx |
Z |
( |
|
|
¯ |
0 )dy = |
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
0 |
0 |
0 |
|
|
|
|
0 |
0 |
|
z2 |
xy |
|
|
|
|
|
|
|
|||
2 |
|
|
3x x2y2 |
2 |
|
|
y3 |
|
|
|
2 |
|
|
|
¯ |
|
|
|
|
|
|
|
|
||
2 |
|
x4 |
|
|
3x |
|
9 7 |
|
|
9 |
|
8 2 |
|
144 |
|
||||||||||
= Z x |
|
dx |
Z |
|
|
dy = Z |
|
( |
|
¯ |
0 |
)dx = Z |
2x dx = |
|
x |
¯ |
0 |
= |
|
: |
|||||
|
2 |
2 |
3 |
16 |
|
||||||||||||||||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
Пример 18.4. Найти объем тела, заданного ограничивающими его поверхностями.
z = 10(x2 + y2) + 1, z = 1 ¡ 20y:
Решение:
В цилиндрических координатах: x =
= rCos', y + 1 = rSin', z = z, íàøå òå-
ло снизу ограничивает параболоид z = 10r2 ¡ ¡ 20rSin' + 11, а плоскость z = 21 ¡ 20rSin'
сверху, как это видно из рис.18.8 Ðèñ. 18.8. Проекция линии пересечения этих поверх-
ностей на плоскость xOy будет в цилиндри- ческих координатах: 10r2 ¡ 20rSin' + 11 = 21 ¡ 20rSin' èëè
r = 1.
Тогда искомый объем находим тройным интегралом
2¼ |
1 |
21¡20rSin' |
2¼ |
1 |
¯ |
21¡20rSin' |
|
0 |
0 |
¡ |
|
0 |
0 |
||
V = Z d' Z rdr |
|
Z |
dz = Z |
d' Z r(z |
¯ |
10r2¡20rSin'+11) dr = |
|
|
2 |
10r2 20rSin'+11 |
|
|
|
||
|
|
|
|
¯ |
|
||
Z¼ Z1
= d' r(21 ¡ 20rSin' ¡ 10r2 + 20rSin' ¡ 11)dr =
00
= |
Z |
d' Z r( ¡ r )dr = |
|
Z |
( |
2r ¡ |
4r ) |
0 d' = |
|||||||||||||
|
2¼ |
|
1 |
|
|
|
|
|
|
|
2¼ |
|
|
|
|
|
|
|
¯ |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
1 |
2 |
|
|
|
10 |
|
|
1 |
2 |
1 |
4 |
¯ |
1 |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2¼ |
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
Z d' = |
5 |
¯ |
2¼ |
= |
5 |
¼ ( |
êóá |
åä |
:) |
|
|
||||||
|
|
2 |
2 |
' |
0 |
|
: |
|
|
|
|
||||||||||

18.3. Методические указания по решению задач |
269 |
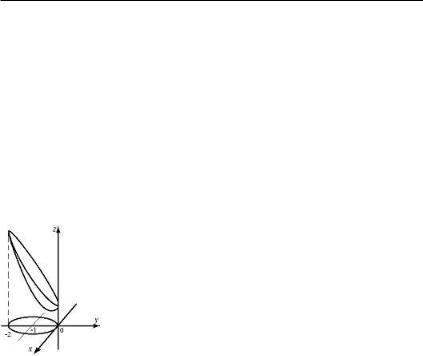
Пример 18.5. . Тело V задано ограничивающими его |
||||||||||||||||||||||||||||||||||||||||
поверхностями, |
|
¹ |
|
|
|
|
плотность. |
|
Найти |
|
массу |
|
|
òåëà. |
||||||||||||||||||||||||||
4(x2 + y2) = z2, x2 + y2 = 1, y = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
z = 0, (y > 0, z > 0), ¹ = 10(x2 + y2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Решение. В цилиндрических координатах |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
x = ½ cos ', |
|
y = ½ sin ', |
|
z = z ìû ïîëó- |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
чим, как видно на рис.18.9, что тело огра- |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
ничено снизу плоскостью z = 0 сверху ко- |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
нической поверхностью z = 2r, а с боков |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
прямым цилиндром r = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
¹ = 10½2¡ в цилиндрической системе |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Искомую массу находим по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
M = Z¼ d' Z1 |
½d½ |
2Z½ ¹dz = 10 Z¼ d' Z1 |
½3d½ |
2Z½ dz = |
|
|
Ðèñ. 18.9. |
|
||||||||||||||||||||||||||||||||
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
¼ |
1 |
½ ½d½ == |
¼ |
|
|
|
|
|
|
|
|
|
|
|
0) = |
|
¼ |
( |
: |
|
|
|
|
|
): |
|||||||||||||
|
|
Z d' Z |
|
Z d'( 5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
½5 |
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
10 |
|
|
|
32 |
|
|
|
|
|
20 |
R |
|
|
|
|
|
|
|
¯ |
1 |
|
4 |
|
ед массы |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¡ |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 18.6. Вычислить L |
|
|
|
dl |
|
, åñëè L отрезок прямой |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
x |
|
|
y |
|||||||||||||||||||||||||||||||||||||
y = 1x 2, заключенный между точками A(0, 2) è B(4,0). |
|
|
||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1. Подставим вместо |
||||||||||||
Решение. Находим производную y0 |
||||||||||||||||||||||||||||||||||||||||
переменной y функцию y = 1x 2. |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
= p |
|
|
Z |
|
= p |
|
|
|
ln jx + 4j ¯ |
0 = p |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
5 |
5 |
|
|
|
ln : |
|
|
|||||||||||||||||||||||||||||
|
|
x ¡ y |
x + 4 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
L |
|
|
|
|
|
0 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
4 |
|
|
5 |
|
|
2 |
|
|
|
||||
|
|
|
dl |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
||||||||||
параболы y = x от точки A(1,1) äî |
|
R |
2 |
¯ |
|
|
|
, |
|
|
ãäå |
|
|
äóãà |
||||||||||||||||||||||||||
|
|
B(2,4). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Пример 18.7. |
Вычислить интеграл |
|
L |
|
|
|
|
|
|
|
|
|
|
L |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x dx + xydy |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Z x2dx + xydy = Z |
x2 + 2x4 |
|
|
3 |
+ 25 |
¶¯ |
|
|
= |
|
|
|||||||||||||||||||||||||||||
dx = µ |
1 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
¡ |
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
¯ |
2 |
|
|
|
|
||||||
L |
|
|
|
|
|
|
|
8 |
|
1 |
|
|
|
|
|
|
|
|
|
x3 |
|
x5 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1411 |
|
|
|
¯ |
|
|
|
|
|
||||
|
|
|
|
|
|
= ³3 + |
|
³3 |
|
|
|
´ = |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
5 |
´ ¡ |
|
+ |
5 |
|
15: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||

270 |
Лекция 18. Тройные и криволинейные интегралы |
18.4. Примеры для самостоятельного решения
вания |
ограничена |
RRR |
dxdydz |
|
|
|
||||
1. |
Вычислить |
|
|
|
|
|
|
|
||
|
(x + y + z + 1)3 , если область |
интегриро- |
||||||||
x + y + z = 1. |
координатными плоскостями и |
плоскостью |
||||||||
|
|
|
|
|
|
|
||||
2. |
Вычислить a dx x dy y xyzdz= |
x |
+ y |
+ |
||||||
|
|
Вычислить R |
|
R |
R |
|||||
3. |
0 |
0 |
0 |
|
|
2 |
2 |
|||
объем тела, ограниченного сферой |
||||||||||
+ z2 =4 и поверхностью параболоида x2 + y2 =3z. |
|
|
|
|||||||
4. |
Вычислить объем тела, ограниченного поверхностями z = |
|||||||||
p |
|
|
|
|
|
|
|
|
|
|
=x2 + y2 , z = x2 + y2.
5.Вычислить объем тела, ограниченного плоскостью z = 0,
цилиндрической поверхностью x = |
x2 + y2 |
и сферой x2 + y2 + |
|
2 |
|||
+ z2 = 4 (внутри цилиндра). |
|
||
|
|
6.Определить объем тел, ограниченных поверхностями: z =
=x2 + y2; x2 + y2 + z2 = 2.
7.Определить объем тел, ограниченных поверхностями: x2 +
+y2 ¡ z2 = 0, z = 6 ¡ x2 ¡ y2.
8.Определить объем тел, ограниченных поверхностями: az =
= x2 + y2; z2 = x2 + y2.
9. Определить объем тел, ограниченных поверхностями: 3z =
= x2 + y2; z = 3. |
|
|
|
|
|
|
|
|
|
|
||
10. |
Определить объем тел, ограниченных поверхностями: |
|||||||||||
z = x2 + y2; y = x2, y = 1, z = 0. |
C |
|
D |
|
||||||||
вершинами в |
|
H |
A |
|
|
B |
|
|
|
|||
11. |
Вычислить |
|
xydl, åñëèL |
|
контур прямоугольника с |
|||||||
|
|
точках |
|
(0,0), |
|
(4,0), |
|
(4,2), |
|
(0,2). |
||
= a(t sint), y = a(1R p t)(a |
|
|
|
|
|
|
|
|||||
12. |
Вычислить |
L |
2y dl, åñëè L первая арка циклоиды x = |
|||||||||
|
|
|
|
|||||||||
|
|
|
|
cos |
>0). |
|
|
|
|
|||
A(1,0,1) è B(2,2,3).R |
|
|
|
|
|
|
|
|
||||
13. |
Вычислить |
L xyzdl, åñëè L ¡ ¡ отрезок прямой между |
||||||||||
14.R Вычислить:
xdl, åñëè L отрезок прямой, соединяющий точки A(0,0)
L
è B(1,2).

18.4. Примеры для самостоятельного решения |
271 |
18.4.1. |
Ответы. 1. 32. 2. 125. 3. 9. |
4. 1 |
|
|
1 |
64 2. |
|||||||
|
|
|
3 |
6 |
± |
2 |
2 |
¡ e . 5.. 6. 3 a |
|||||
4¼apa . 13.212. 14. p5 2. |
9. 10a2 |
3. 10. a2(¼ |
¡ |
1). 1124. 12. |
|||||||||
7. 2/3. 8. |
1(15 ¡ 16 ln 2). |
|
|
||||||||||
|
|
|
|
|
± |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
