1.3.3. Биномиальное распределение

Дискретная СВ Xраспределена по биномиальному закону, если она принимает значения 0, 1, 2, …,nс вероятностями:

(1.33)

где 0 < p< 1,q= 1 –p,m= 0, 1, …,n.

Из схемы Бернулли следует, что СВ X – число появлений событияАв серии изnнезависимых опытов, в каждом из которых событиеАможет появиться с вероятностьюp, имеет биномиальное распределение. Для СВX, имеющей биномиальное распределение с параметрамиpиn,

M(X) =np,D(X) =npq, (1.34)

где q= 1 –p.

Следует отметить, что гипергеометрическое распределение при nмалых по сравнению сN(практически приn< 0,1N) приближается к биномиальному распределению с параметрамиnи

Замечание 1.Для вычисленияпри достаточно большихnиmприменима формула Стирлинга:

Замечание 2.Для биномиальных вероятностей справедлива рекуррентная формула:

Замечание 3.Наиболее вероятное число успеховK₀в серии изnнезависимых испытаний удовлетворяет неравенству:

np –q≤K₀<np+p.

1.3.4. Предельные теоремы

При большом числе испытаний непосредственное вычисление вероятностей P(X=m) иP(m₁≤X ≤m₂) для СВX, распределено по биномиальному закону, становится громоздким, так как факториалы, входящие в формулубудут очень большими числами. В этом случае для вычисления указанных вероятностей можно использовать асимптотические (предельные) формулы.

Когда оба параметра pиqзаметно отличны от 0, применяются локальная (1.35, 1.36) и интегральная формулы Муавра-Лапласа (1.38, 1.40).

(1.35)

где

(1.36)

– плотность нормированной нормальной СВ X, а

(1.37)

(1.38)

где

(1.39)

– функция Лапласа,

(1.40)

Имеются таблицы значений (x) (таблица 1) и(x) (npq> 20) (таблица 2).

С помощью этих формул при n100 иnpq> 20, как правило, удается получить искомые вероятности с точностью до трех-четырех знаков после запятой.

1.3.5. Распределение Пуассона

Дискретная СВ Xназываетсяраспределенной по закону Пуассона, если ее возможные значения 0, 1, 2, …,m, …, а вероятность события (X=m) выражается формулой

, (1.41)

где a> 0. Распределение Пуассона зависит от одного параметраа. Для СВX, распределенной по закону Пуассона,

M(X) =D(X) =a, (1.42)

т. е. параметр aпуассоновского распределения равен одновременноM(X) иD(X). В этом состоит отличительная особенность распределения Пуассона, которая используется на практике (на основании опытных данных находят оценки дляM(X) иD(X); если они близки между собой, то есть основание считать, что СВXраспределена по закону Пуассона).

Пуассоновское распределение является предельным для биномиального при p0,n, еслиnp=a=const. Этим распределением можно пользоваться приближенно, если производится большое число независимых опытов, в каждом из которых событиеAпроисходит с малой вероятностью. Примерами СВX, имеющих распределение Пуассона, являются: число опечаток в большом тексте, число бракованных деталей в большой партии; число-частиц, испускаемых радиоактивным источником и т. д. При этом считается, что события появляются независимо друг от друга с постоянной интенсивностью, характеризующейся параметромa=np.

Замечание.Имеются специальные таблицы, пользуясь которыми можно найтиP_m, знаяmиa.

Распределение Пуассона встречается при рассмотрении потоков событий. Потоком событийназывается последовательность однородных событий, наступающих одно за другим в случайные моменты времени.

Среднее число событий , приходящееся на единицу времени, называетсяинтенсивностью потока. Величинаможет быть как постоянной, так и переменной = (t).

Поток событий называется потоком без последействия, если вероятность попадания того или иного числа событий на какой-либо участок времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним участок.

Поток событий называется ординарным, если вероятность появления на элементарном участке времениtдвух или более событий пренебрежимо мала по сравнению с вероятностью появления одного события. Ординарный поток событий без последствия называетсяпуассоновским.Если события образуют пуассоновский поток, то числоXсобытий, попадающих на любой участок времени (t₀,t₀+), распределено по закону Пуассона:

где a– математическое ожидание числа событий, попадающих на участок:

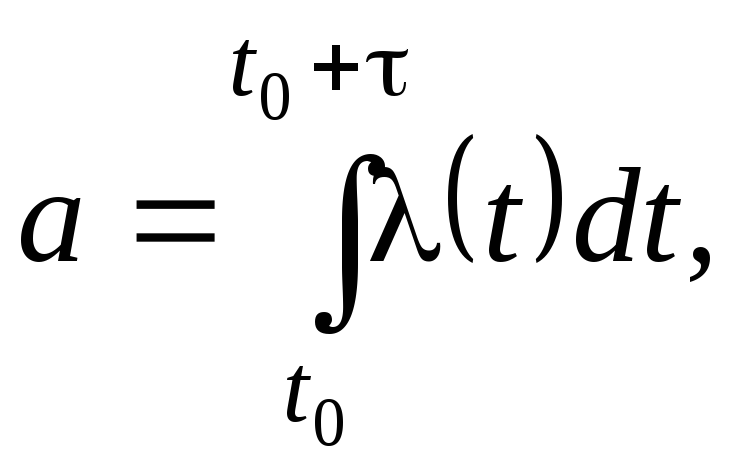
где (t) – интенсивность потока.

Если =const, то пуассоновский поток называетсястационарнымпуассоновским илипростейшим. Для простейшего потока число событий, попадающих на любой участок времени длины, распределено по закону Пуассона с параметрома=.

В качестве примеров потоков можно рассматривать поступления вызовов на АТС, на пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового обслуживания, последовательность отказов элементов некоторого устройства.