2.4. Произвольные непрерывные распределения

Пример 1. Непрерывная СВXзадана функцией распределения

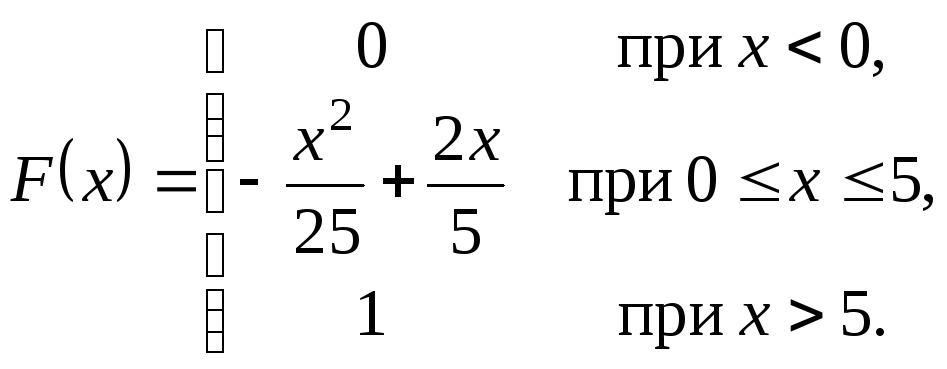
Найти: 1) плотность распределенияf(x); 2)M(X); 3)P(1 <X< 2); 4) найти вероятность того, что в трех независимых испытаниях СВXпримет ровно два раза значения из интервала (1, 2).

Решение. 1) Найдем.

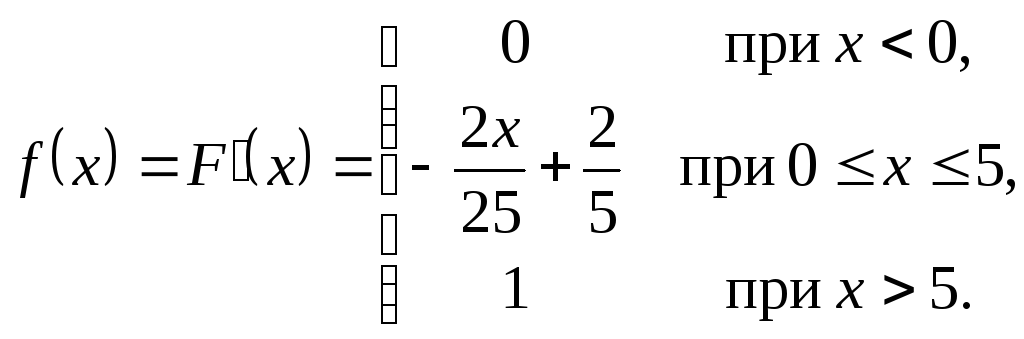
2) Используя формулу (1.17) для нахождения математического ожидания непрерывной СВ X, найдем

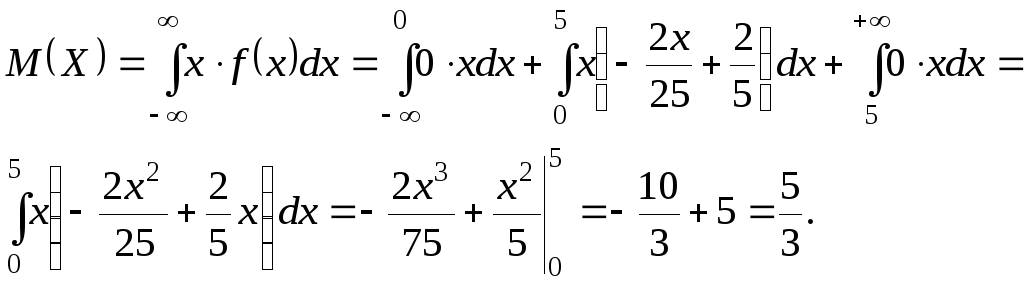
3) Вероятность того, что СВ Xпримет значения, заключенные в интервале (1, 2), по формуле (1.10) равна

4) Для нахождения искомой вероятности применим формулу Бернулли. Здесь n= 3,m= 2,p= 0,28,q= 1 –p= 0,72.

Пример 2. Задана функцияf(x)

Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой СВ X. НайтиF(X),P(1 <X< 3),M(X),D(X).

Решение. Используя свойство нормированности плотности распределения, определим значение параметраA, при котором данная функция задает плотность распределения вероятности некоторой непрерывной СВX.

Тогда

Найдем функцию распределения F(x), используя формулу (1.10)

При x(–, 0]

при x(0, 2]

при x> 2

Имеем

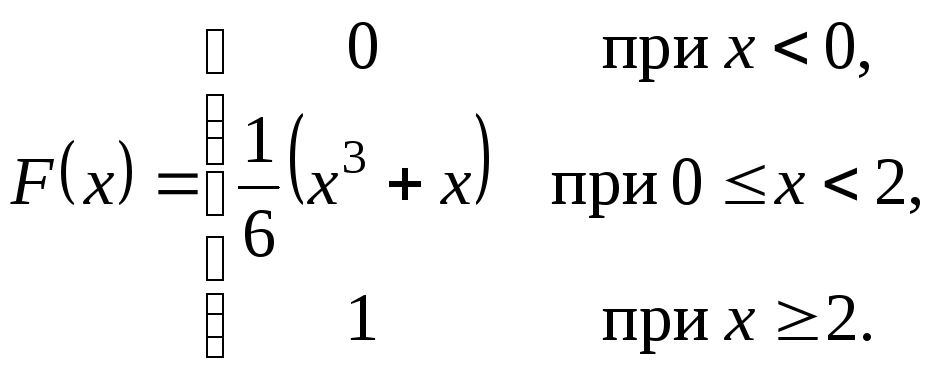
Найдем числовые характеристики:

2.5. Нормальное, равномерное и показательное распределения

Пример 1. Математическое ожидание нормально распределенной непрерывной СВXM(X) = 6, а среднее квадратическое отклонение(X) = 2.

Найти: 1) вероятность попадания значений СВ Xв интервал (2; 9);

2)

3) интервал, симметричный относительно a, в который попадают значения СВXс вероятностью= 0,9642.

Решение.1) Найдем вероятность попадания значений СВX в интервал (2; 9).

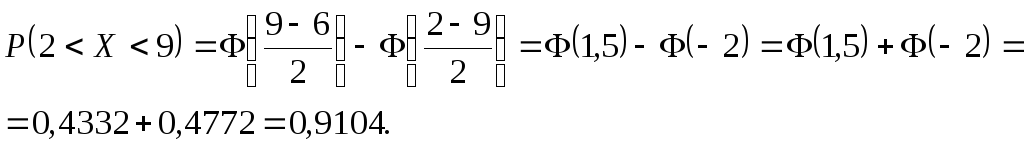
Значения функции Лапласа взяты из таблицы. Учтено свойство нечетности функции Ф(–X) = – Ф(X).

2) Определим вероятность

Так как a=M(X) = 6 и=(X) = 2, то

3) Найдем интервал, симметричный относительно a, в который попадают значения СВXс вероятностью= 0,9642.

Из таблицы значений функции Лапласа находимто есть= 4,2. Тогда интервал равен –4,2 <X– 6 < 4,2 и 1,8 <X< 10,2.

Пример 2. Случайная величинаТ (час.) – время безотказной работы прибора имеет показательное распределение. Найти вероятность того, что прибор проработает без ремонта не менее 600 часов, если среднее время безотказной работы приборов этого типа равно 400 часам.

Решение.M(T) = 400 час., следовательно, по формуле (1.46)Так как для показательного распределениято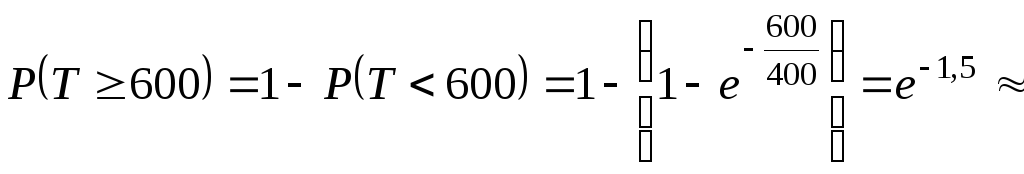0,2233.

Пример 3. Случайная величинаXраспределена равномерно на отрезке [a,b]. Найти вероятность попадания случайной величиныXна отрезок [,], целиком содержащийся внутри отрезка [a,b].

Решение. Воспользуемся формулойгде плотность вероятности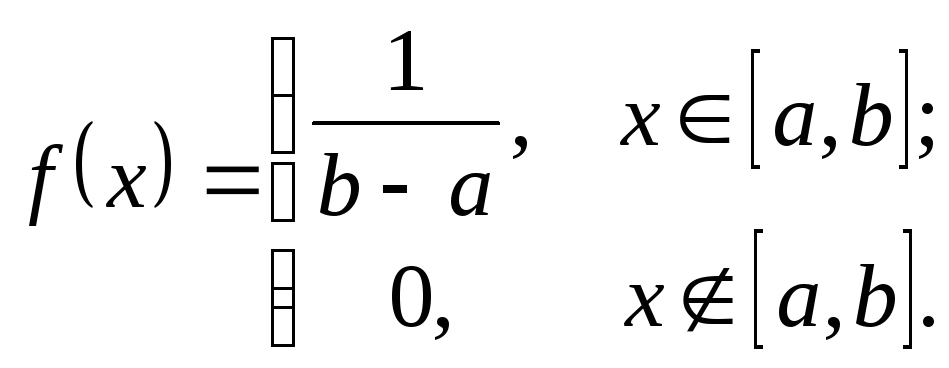

Тогда

.

Таким образом

Пример 4. Электропоезда идут строго по расписанию с интервалом 20 мин. Найти вероятность того, что пассажир, подошедший к платформе, будет ожидать очередной электропоезд более 10 мин., а также среднее время ожидания.

Решение.X– время ожидания (мин.) электропоезда, можно считать равномерно распределенной случайной величиной с плотностью:

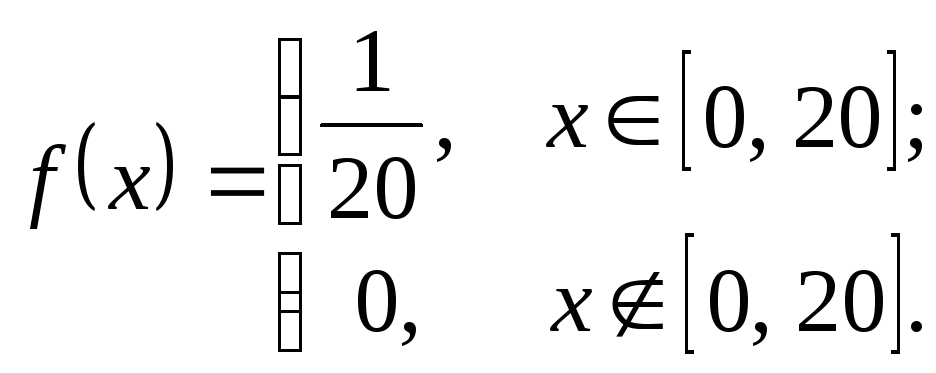
Тогда

и это среднее время ожидания электропоезда.

Пример 5. Автомат изготовливает втулки. Втулка считается годной, если отклонениеXее диаметра от проектного размера по абсолютной величине меньше 1мм. Считая, что случайная величинаXраспределена нормально со средним квадратическим отклонением= 0,5 мм и математическим ожиданиемa= 0, найти сколько будет годных втулок среди 100 изготовленных, а так же вероятность того, что отклонение от проектного размера будет не менее 0,4 мм и не более 0,8 мм.

Решение. Воспользуемся формулой ( )при= 1,= 0,5 иa= 0.

Получим

Отсюда следует, что примерно 95 втулок из 100 окажутся годными.

Для нахождения вероятности того, что отклонение от проектного размера будет не менее 0,4 мм и не более 0,8 мм воспользуемся формулой (1.54)

приa = 0,  = 0,5,  = 0,4,  = 0,8.

Значения функции Ф(x) находим по таблице.