1.2.4. Центрированные и нормированные случайные величины

Центрированной случайной величиной, соответствующей СВ X называется разность между случайной величиной X и ее математическим ожиданием

(1.23)

Случайная величина называется нормированной, если ее дисперсия рана 1. Центрированная и нормированная случайная величина называетсястандартной.

Стандартная случайная величина Z, соответствующая случайной величинеXнаходится по формуле:

(1.24)

1.2.5. Другие числовые характеристики

Мода дискретной СВ Xопределяется как такое возможное значениеx_m, для которого

(1.25)

Модой непрерывной СВ X называется действительное число M₀(X), определяемое как точка максимума плотности распределения вероятностей f(x).

Таким образом, мода СВ Xесть ее наиболее вероятное значение, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь несколько значений (мультимодальное распределение).

Медианой непрерывной СВ Xназывается действительное числоM_D(X), удовлетворяющее условию

(1.26)

Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.

Начальным моментом m-го порядка СВX (если он существует) называется действительное число_m, определяемое по формуле

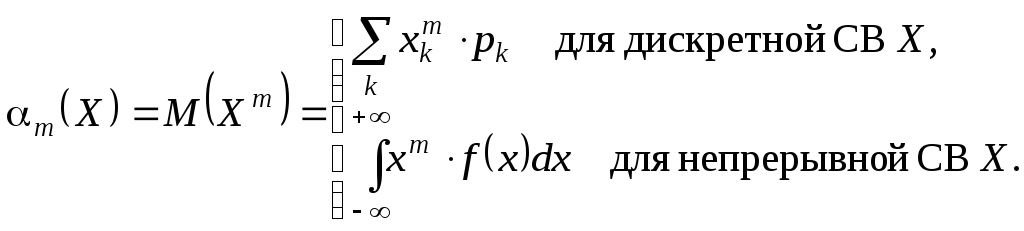(1.27)

Центральным моментом m-го порядка СВ X(если он существует) называется число_m, определяемое по формуле

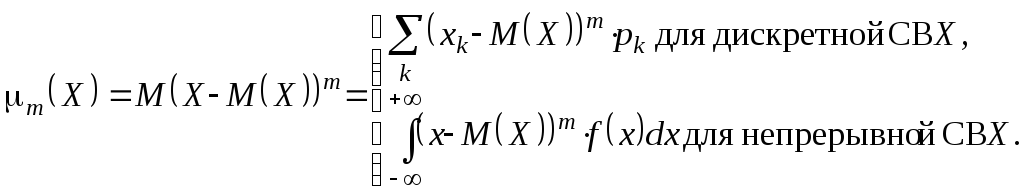(1.28)

Математическое ожидание СВ Xесть ее первый начальный момент, а дисперсия – второй центральный.

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков.

Коэффициентом асимметрии ("скошенности") А(X)называется величина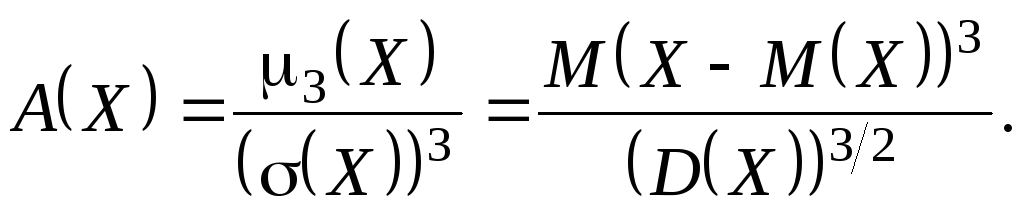

Коэффициентом эксцесса ("островершинности") E(X) СВ Xназывается величина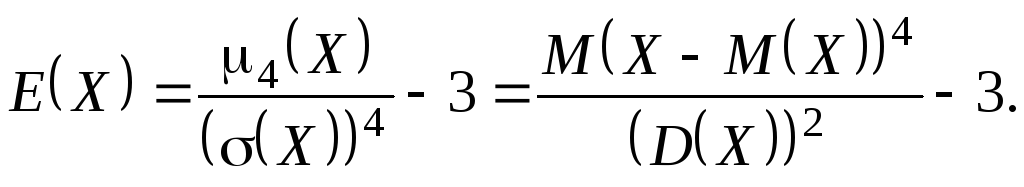

1.3. Некоторые законы распределения дискретных случайных величин

1.3.1. Геометрическое распределение

Дискретная СВ Xимеет геометрическое распределение, если ее возможным значениям 0, 1, 2, …,m, … соответствуют вероятности, вычисляемые по формуле

(1.29)

где 0 < p< 1,q= 1 –p.

На практике геометрическое распределение встречается, когда производится ряд независимых попыток достигнуть какого-то результата Аи вероятность появления событияАв каждой попыткеP(A) =P. СВX– число бесполезных попыток (до первого опыта, в котором появится событиеА), имеет геометрическое распределение с рядом распределения:

xi	0	1	2	…	m	…
pi	p	qp	q2p	...	qmp	…

и числовыми характеристиками:

(1.30)

1.3.2. Гипергеометрическое распределение

Дискретная СВ Xс возможными значениями 0, 1, …,m, …,Mимеет гипергеометрическое распределение с параметрамиN,M,n, если

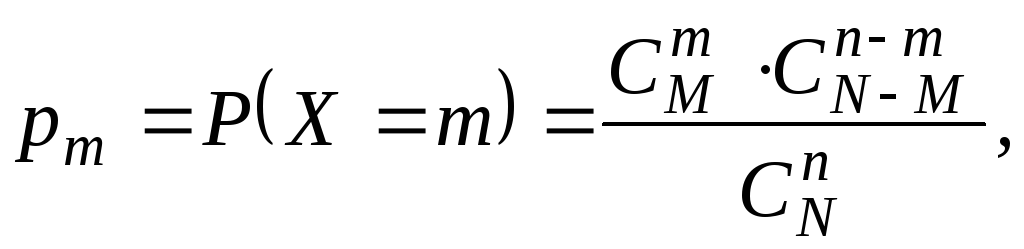(1.31)

где M≤N,m ≤n,n≤N,m,n,N,M– натуральные числа.

Гипергеометрическое распределение возникает в случаях, подобных следующему: имеется Nобъектов, из которыхMобладают определенным признаком. Из имеющихсяNобъектов наудачу выбираютсяnобъектов.

СВ X – число объектов с указанным признаком среди выбираемых, распределена по гипергеометрическому закону.

Гипергеометрическое распределение используется, в частности, при решении задач, связанных с контролем качества продукции.

Математическое ожидание случайной величины, имеющей гипергеометрическое распределение, равно:

(1.32)