
- •Нина Александровна Дашко
- •Часть 1
- •1. ВВЕДЕНИЕ
- •1.1. Состав и строение атмосферы
- •1.2. История развития метеорологии как физической науки
- •1.2.1. Древнегреческий период развития науки
- •1.2.2. Эллинистический период развития науки
- •1.2.3. Простонародная метеорология
- •1.2.4. Развитие науки на Востоке
- •1.2.5. Развитие научных связей Европы и Востока
- •1.2.6. Изобретение метеорологических приборов
- •1.2.6. Научные общества и академии
- •1.3. Развитие синоптической метеорологии
- •1.4. ВМО – Всемирная метеорологическая организация
- •1.5. Гидрометеорологическая служба России
- •2. МЕТЕОРОЛОГИЧЕСКАЯ ИНФОРМАЦИЯ
- •2.1. Требования к гидрометеорологической информации
- •2.2. Виды гидрометеорологической продукции
- •2.3. Потребители гидрометеорологической информации:
- •2.4. Кодирование гидрометеорологической информации
- •2.4.1. Структура кода КН-01
- •Схема кода КН-01:
- •Раздел 0
- •Раздел 1
- •Раздел 2 – для судовых или буйковых станций
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 0
- •Для сухопутных станций:
- •Передача судовых данных:
- •Раздел 1 (для станций любого типа)
- •Раздел 2 (используется при передаче судовых данных)
- •Раздел 3
- •Раздел 4 (для высокогорных станций)
- •Раздел 5
- •2.4.2. Структура кода КН-04
- •ЧАСТЬ "A" КОДА КН-04
- •ЧАСТЬ "B" КОДА КН-04
- •Особые точки по температуре воздуха:
- •Особые точки по ветру:
- •3. СОСТАВЛЕНИЕ КАРТ ПОГОДЫ
- •3.1. Виды карт погоды
- •3.2. Приземные карты погоды (составление и чтение)
- •Раздел 1
- •Раздел 2
- •Раздел 3
- •3.3. Составление высотных карт погоды
- •3.3.1. Геопотенциал
- •3.3.2. Барометрическая формула геопотенциала
- •3.3.3. Барометрическая ступень
- •3.3.4. Карты барической топографии
- •3.4. Составление вспомогательных карт погоды
- •4. АНАЛИЗ КАРТ ПОГОДЫ
- •4.1. Первичный анализ приземных карт погоды
- •4.1.1. Правила оформления приземной карты погоды
- •4.1.2. Проведение атмосферных фронтов на картах погоды
- •4.2. Первичный анализ высотных карт погоды
- •4.2.1.Правила оформления высотных карт погоды
- •4.2.3. Анализ карт относительной топографии
- •4.3. Анализ вспомогательных карт погоды
- •5. АЭРОЛОГИЧЕСКИЕ ДИАГРАММЫ И ВЕРТИКАЛЬНЫЕ РАЗРЕЗЫ АТМОСФЕРЫ
- •5.1. Аэрологические диаграммы
- •5.1.2. Построение аэрологической диаграммы
- •5.1.3. Анализ аэрологической диаграммы
- •5.1.4. Графические расчёты с помощью аэрологических диаграмм
- •5.2. Вертикальные разрезы атмосферы
- •5.2.1. Правила построения вертикальных разрезов атмосферы
- •5.2.2. Анализ вертикальных разрезов атмосферы
- •5.2.3. Временные разрезы атмосферы
- •Температура воздуха, °С
- •6. ОШИБОЧНЫЕ ДАННЫЕ НА КАРТАХ ПОГОДЫ
- •7. ПРИНЦИПЫ СИНОПТИЧЕСКОГО АНАЛИЗА
- •7.1. Основные синоптические объекты
- •7.2. Информативность карт барической топографии
- •7.4. Обзор синоптического положения за предыдущие сутки
- •8.1. Вычисление производных
- •8.2.1. Прямолинейная интерполяция
- •8.2.2. Криволинейная интерполяция
- •8.2.3. Формальная экстраполяция
- •8.3.1. Траектории воздушных частиц
- •Способ обратного переноса:
- •Рис. 8.4. Способ обратного переноса
- •Способ прямого переноса:
- •8.3.2. Линии тока воздушных частиц
- •9. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОЛЕЙ МЕТЕОРОЛОГИЧЕСКИХ ВЕЛИЧИН
- •9.1.1. Градиент метеорологической величины
- •9.2. Поле атмосферного давления
- •9.2.3. Локальные изменения давления
- •9.3. Динамические изменения давления воздуха
- •9.4. Распределение атмосферного давления на Земном шаре
- •9.5. Поле ветра
- •Цилиндрическая система координат
- •Сферическая система координат
- •Натуральная система координат
- •9.5.2. Силы, действующие в атмосфере
- •Сила барического градиента
- •Отклоняющая сила вращения Земли
- •Сила трения
- •Центробежная сила
- •9.6. Уравнения движения
- •9.6.1. Геострофический ветер
- •9.6.3. Градиентный ветер
- •9.6.4. Действительный ветер
- •9.7. Особенности ветрового режима над Японским морем
- •9.8. Особенности ветрового режима над Охотским морем
- •9.9. Дивергенция и вихрь скорости
- •9.9.1 Дивергенция вектора скорости ветра
- •9.9.2. Вихрь вектора скорости ветра
- •9.9.3. Уравнение тенденции вихря скорости
- •Характерные синоптические масштабы:
- •9.9.5. Уравнение дивергенции скорости
- •9.10. Поле вертикальных движений атмосферы
- •9.10.1. Классификация вертикальных движений атмосферы
- •9.10.2. Упорядоченные вертикальные движения атмосферы
- •9.10.3. Расчёт вертикальных движений атмосферы
- •9.11. Поле температуры воздуха
- •9.11.1. Температурные градиенты
- •9.11.2. Адиабатические изменения температуры воздуха
- •9.11.3. Термический ветер
- •9.11.4. Локальные изменения температуры воздуха
- •10. ВОЗДУШНЫЕ МАССЫ
- •10.1. Масштабы воздушных масс
- •10.2. Очаги формирования воздушных масс
- •10.3. Географическая классификация воздушных масс
- •10.5. Трансформация воздушных масс
- •10.6. Термодинамическая классификация воздушных масс
- •10.7. Характеристики устойчивых воздушных масс
- •10.7.1. Тёплая устойчивая воздушная масса
- •10.7.2. Холодная устойчивая воздушная масса
- •10.8. Характеристики неустойчивых воздушных масс
- •10.8.1. Тёплая неустойчивая воздушная масса
- •10.8.2. Холодная неустойчивая воздушная масса
- •10.9. Оценка устойчивости воздушных масс
- •11. АТМОСФЕРНЫЕ ФРОНТЫ
- •11.1. Ориентация и размеры фронтальной поверхности
- •11.2. Классификация фронтов
- •11.2.1. Географическая классификация атмосферных фронтов
- •11.3. Перемещение фронтов
- •11.4. Профиль движущегося фронта
- •11.5. Общие характеристики фронтов
- •11.5.1. Фронты в барическом поле
- •11.5.2. Фронты в поле ветра
- •11.5.3. Фронты в поле барических тенденций
- •11.5.4. Фронты в поле температуры воздуха
- •11.5.5. Фронты в поле влажности и облачности
- •11.6. Тёплый фронт
- •11.7. Холодный фронт
- •11.7.1. Холодные фронты 1-го рода
- •11.7.2. Холодные фронты 2-го рода
- •11.7.3. Вторичные холодные фронты
- •11.8. Фронты окклюзии
- •11.8.1. Облака и осадки холодного фронта окклюзии
- •11.8.2. Облака и осадки тёплого фронта окклюзии
- •11.10. Образование и размывание атмосферных фронтов
- •11.10.3. Оценка тропосферного фронтогенеза и фронтолиза
- •11.10.4. Приземный фронтогенез и фронтолиз
- •12. ЦИКЛОНЫ И АНТИЦИКЛОНЫ УМЕРЕННЫХ ШИРОТ
- •12.1. Основные определения
- •12.1.1. Вертикальная протяжённость барических образований
- •12.1.2. Оси барических образований
- •12.1.3. Фронтальные и нефронтальные барические образования
- •Модель циклона по Ли
- •Модель циклона по Бьеркнесу и Сульбергу
- •Основные теории возникновения циклонов
- •Конвекционная теория циклонов
- •Механическая теория циклонов
- •Волновая теория циклонов
- •Дивергентная теория циклонов
- •12.2. Условия возникновения барических образований
- •12.3. Стадии развития циклонов
- •12.3.1. Начальная стадия развития циклона
- •12.3.2. Стадия молодого циклона
- •12.3.3. Стадия максимального развития циклона
- •12.3.4. Стадия окклюдирования циклона
- •12.3.5. След циклона
- •12.3.6. Серии циклонов
- •12.4. Стадии развития антициклонов
- •12.4.1. Начальная стадия развития антициклона
- •12.4.2. Стадия молодого антициклона
- •12.4.3. Стадия максимального развития антициклона
- •12.4.4. Стадия разрушения антициклона
- •12.5. Регенерация барических образований
- •12.5.1. Регенерация циклонов
- •12.5.2. Регенерация антициклонов
- •12.6. Перемещение барических образований
- •12.7. Центры действия атмосферы
- •Постоянные центры действия атмосферы:
- •Сезонные центры действия атмосферы:
- •12.7.1. Характеристика ЦДА Северо-Атлантического региона
- •Азорский антициклон
- •Исландская океаническая депрессия
- •12.7.2. Характеристика ЦДА Северной Америки
- •Канадский максимум
- •Калифорнийский минимум
- •12.7.3. Характеристика ЦДА Азиатско-Тихоокеанского региона
- •Азиатский антициклон
- •Алеутский минимум
- •Южноазиатская депрессия
- •Северотихоокеанский антициклон
- •Переходные зоны между центрами действия атмосферы
- •12.7.4. Летние синоптические процессы над Охотским морем
- •12.8. Погода в циклонах на разных стадиях развития
- •12.8.1. Погода в передней части молодого циклона
- •12.8.2. Погода в тёплом секторе молодого циклона
- •12.8.3. Погода в тыловой части молодого циклона
- •12.8.4. Погода в окклюдированном циклоне
- •12.9. Погода в антициклонах
- •12.9.1. Инверсии в антициклонах
- •12.9.2. Фронты в антициклоне
- •12.9.3. Погода в антициклоне
- •13. ВЛИЯНИЕ ОРОГРАФИИ НА АТМОСФЕРНЫЕ ПРОЦЕССЫ
- •13.1. Горные ветры
- •Бора
- •13.2. Облакообразование и осадки
- •13.3. Влияние орографии на атмосферные фронты
- •14. СТРУЙНЫЕ ТЕЧЕНИЯ
- •15. ПРОГНОЗ СИНОПТИЧЕСКОГО ПОЛОЖЕНИЯ
- •15.3. Прогноз эволюции барических образований
- •15.4. Прогноз возникновения новых барических образований
- •15.5. Прогноз перемещения и эволюции атмосферных фронтов
- •15.6. Расчёт давления в точках поля
- •15.6.1. Адвективный способ расчёта давления в точках поля
- •15.7. Оценка приземной прогностической карты
- •16.1. О прогнозе погоды в США и Японии
- •16.1.1. Служба погоды в США
- •16.1.2. Служба погоды в Японии
- •Примечание 1
- •Примечание 2
- •Примечание 3
- •17.1. Критерии определения объёма выборки
- •17.2. Определение свойств выборки
- •17.3. Законы распределения метеорологических величин
- •17.3.2. Нормальный закон распределения
- •17.4. Точность и достоверность оценок выборки
- •17.5. Анализ статистических характеристик
- •17.5.1. Исследование трендовой составляющей
- •17.5.3. Процентили
- •17.5.4. Приёмы аппроксимации
- •17.6.1. Выбор предикторов
- •17.6.2. Формирование обучающей выборки
- •17.6.3. Корреляционный анализ
- •17.6.5. Отбор информативных предикторов
- •17.7.1. Оценки свойств уравнений регрессии
- •17.7.2. Применение пошаговой процедуры расчета
- •17.7.3. Процедура отбора оптимальных уравнений
- •17.11. Статистическая оценка прогнозов
- •17.11.1. Количественные прогнозы
- •17.11.2. Альтернативные прогнозы
- •18.1. Прогноз температуры воздуха у поверхности Земли
- •18.1.1. Адвективные изменения температуры воздуха
- •18.1.2. Трансформационные изменения температуры воздуха
- •18.1.3. Суточный ход температуры воздуха
- •18.2. Прогноз влажности воздуха у поверхности Земли
- •СОДЕРЖАНИЕ
- •АТМОСФЕРНЫЕ ФРОНТЫ
- •СТРУЙНЫЕ ТЕЧЕНИЯ
17. Математическая статистика в синоптической метеорологии |
36 |
17.7.3. Процедура отбора оптимальных уравнений
Выбираются уравнения, оценки которых дают следующие результаты: шаг, на котором увеличивается коэффициент множественной корреляции (R), оставаясь затем на последующих шагах практически постоянным.
Шаг, на котором показатель остаточной суммы квадратов отклонений от регрес-
сии (SSr ) испытывает наибольшие изменения по сравнению с предшествующим и последующим шагами.
Шаг, на котором доля изменчивости, предсказанная регрессией, или предска-
занная сумма квадратов отклонений (SS d ), увеличивается с наибольшим вкладом.
Шаг, на котором остаточный средний квадрат ошибки уравнения регрессии
( M sr ) стабилизируется – т.е. уменьшение остаточной суммы квадратов отклонений компенсируется уменьшением числа степеней свободы κr или увеличением числа объясняющих переменных р.
Средняя квадратическая ошибка (S ) резко меняется от данного шага к следующему, а на остальных шагах при включении дополнительных членов уравнения остается практически неизменной.
F-критерий, в целом отражающий суммарный эффект ухудшения схемы при невключении данного предиктора или улучшения ее при его включении, начинает убывать.
Наиболее информативным для статистического анализа качества уравнений рег-
рессии являются показатели SSr , F, R, S , на них следует обращать особое внимание при выборе оптимальных уравнений связи.
Атмосферные процессы нестационарны, поэтому диагностические статистические зависимости теряют с течением времени свою значимость. Для преодоления подобных трудностей необходимо обновление исходной выборки по мере пополнения архива, непосредственно примыкающих к срокам прогноза.
17.8.Пример построения линейных уравнений
вслучае двух и трёх переменных
Рассмотрим линейную связь между двумя переменными Y и X. Общий вид уравнения регрессии (связи) в этом случае –
y = ax + b ,
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
37 |
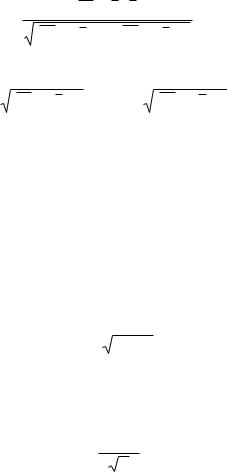
где a – коэффициент линейной регрессии, b – свободный член
Из аналитической геометрии известно, что если прямые проходят через некото-
−−
рую точку с координатами ( x, y ), то уравнения этих прямых имеют вид:
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|||||||
|
|
|
|
|
|
|
|
y − y = a(x − x) . |
||||||||||||||||||||||||
Коэффициент корреляции рассчитывается по формуле: |
||||||||||||||||||||||||||||||||
|
r = |
|
xy − x y |
, |
|
|
||||||||||||||||||||||||||
|
− (x) 2 ] [y2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
[x2 |
− (y)2 ] |
|||||||||||||||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
σx = [x2 − (x) 2 ], |
|
σy = |
[y2 − (y)2 ]. |
|||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
r = |
xy |
x |
y |
, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
σ |
x |
σ |
y |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|||||||
a = |
xy |
x |
y |
|
|
xy |
x |
y |
|
|
|
|
|
|||||||||||||||||||
|
|
|
= |
|
|
|
, b = y − ax . |
|||||||||||||||||||||||||
|
|
|
− ( |
|
2 |
|
|
|
|
σx 2 |
||||||||||||||||||||||
x2 |
|
|
|
|||||||||||||||||||||||||||||
x) |
|
|
|
|||||||||||||||||||||||||||||
Средняя квадратическая ошибка уравнения регрессии:
Sy = ±σy 1 − r2 .
Коэффициент a показывает уровень корреляционной связи данного уравнения.
Средняя ошибка коэффициента корреляции
σr = ± |
1 − r 2 |
. |
|
n |
|||
|
|
Вероятная ошибка коэффициента корреляции
Ey = ±0.67σr .
Тогда вероятное значение коэффициента корреляции заключено в пределах r ± Er .
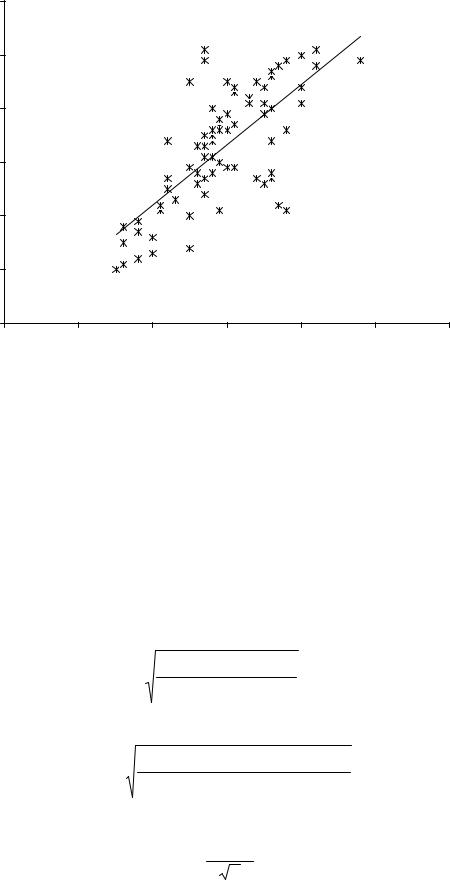
Связь между двумя переменными может быть представлена графически (рис.
17.11):
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
38 |
60
y = 11.18x - 0.18
50
40
Y 30
20
10
0
0 |
1 |
2 |
3 |
4 |
5 |
6 |
X
Рис. 17.11. График связи между двумя переменными X и Y
Уравнение линейной корреляционной связи между тремя переменными имеет
вид
Z = ax + by + c .
Уравнения таких прямых имеют вид:
− − −
z − z = a(x − x)+ b(y − y) .
Коэффициент корреляции рассчитывается по формуле:
R = |
r |
2 |
+ r |
|
2 |
− r |
|
r |
r |
|
zx |
|
zY |
|
zx |
|
zy xy |
||
|
|
|
1 |
− r 2 |
|
|
|
||
|
|
|
|
|
|
xy |
|
|
|
Средняя квадратическая ошибка уравнения регрессии:
1 − rzx |
2 |
− rzy |
2 − rxy |
2 |
+ 2rzx rzy rxy |
|
SZ = ±σZ |
|
1 − rxy 2 |
|
. |
||
Средняя квадратическая ошибка общего коэффициента корреляции:
σR = ± |
1 − R 2 |
. |
|
n |
|||
|
|
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
39 |
Вероятная ошибка коэффициента корреляции:
ER = ±0.67σR .
Коэффициенты a, b и c рассчитывается по формулам:
a = σZ rZX − rZY rXY , b = |
σZ |
|
rZY − rZX rXY , c = z− a x− b y . |
||||||||
|
|
|
|
|
|
|
|
|
− |
− |
− |
|
σX |
1 − rxy 2 |
σY |
|
1 − rxy 2 |
|
|
||||
Для более быстрого решения уравнений регрессии целесообразно сначала опре- |
|||||||||||
− − |
− − − |
|
|
|
|
|
|
||||
делить ( x, y, r, σX , σY ) |
или ( x, y, z, r, σX , σY , σZ ) по имеющимся выборкам перемен- |
||||||||||
ных и подставить известные величины в уравнения для связи между двумя переменными:
|
|
|
|
|
|
|
|
|
|
− |
σY |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = y+ r |
(x − x) , |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
или для связи между тремя переменными: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
− |
σ |
Y |
|
r |
ZX |
− r |
ZY |
r |
XY |
|
− |
|
σ |
Z |
|
r |
ZY |
− r |
ZX |
r |
XY |
− |
z = z+ |
|
|
|
|
|
(x − x)+ |
|
|
|
|
|
(y − y) . |
||||||||||
|
|
|
1 − rXY 2 |
|
|
|
|
1 − rXY 2 |
|
|||||||||||||
|
σX |
|
|
|
|
|
σY |
|
|
|
||||||||||||
17.9.Построение схемы прогноза на основе дискриминантного анализа
Для прогноза метеорологических величин и явлений погоды широко применяются методы параметрического и непараметрического дискриминантного анализа.
Дискриминантные схемы прогноза не указывают непосредственно на количественные оценки метеорологической величины, а дают возможность оценить наличие явления или его отсутствие, например, будет или нет резкое похолодание, произойдет или нет усиление ветра до той или иной градации и др. Такие прогнозы называются альтернативными. Удобно использовать данный подход при прогнозировании явлений погоды, которые трудно выразить количественно – грозы, туманы, гололед и др.
На первом этапе важно выявить синоптические ситуации, метеорологические условия, благоприятствующие наличию или отсутствию данного явления. По сочетанию объясняющих переменных требуется решить, к какому классу можно отнести данное событие.
В зависимости от способа классификации, различают параметрические (локальные) и непараметрические (интегральные) методы дискриминантного анализа.
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
40 |
Впараметрическом дискриминантном анализе принимается, что рассматриваемые объекты извлекаются из нормальных генеральных совокупностей. При значительных отклонениях закона распределения случайной величины от нормального предпочтительнее использование непараметрического дискриминантного анализа.
При применении как параметрического, так и непараметрического дискриминантного анализа положительные результаты следует ожидать, когда выбранные предсказатели хорошо отражают физическую сущность развития явлений погоды.
Вкачестве предикторов выбираются объясняющие переменные, которые наиболее ярко проявляют себя в случае наличия и отсутствия явления. Таким образом необходимо оценить расстояния между классами.
Для оценки репрезентативности предсказателей, позволяющих отнести исходную совокупность признаков к определённому классу, используется расстояние Маха-
лонобиса в случае одной объясняющей переменной ( ∆2 1 ) и двух объясняющих пере-
менных ( ∆2 2 ):
∆21 |
M(x)i − M(x) j |
2 |
|||
= |
|
|
, |
||
σ |
|||||
|
|
|
|
||
|
|
|
1 |
|
|
|
M(x) |
1i − M(x)1j |
|
2 |
M(x)2i − |
M(x)2j |
2 |
||||||||
∆2 2 |
|
|
|
|
|
|
− |
||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|||
1 − r1,2 2 |
|
σ1 |
|
|
|
|
|
σ2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
[M(x) |
1i |
− M(x) |
1j |
] − |
[M(x) |
2i |
|
− M(x) |
2j |
] |
|
|
|
|||||
− 2 |
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
σ1σ2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где
M(x)i – математическое ожидание при наличии явления,
M(x)j – математическое ожидание при отсутствии явления,
σ– среднее квадратическое отклонение.
Впрогностические схемы включаются переменные, дающие наибольший вклад
врасстояние Махалонобиса.
Затем строится уравнение дискриминантной функции (решающее правило):
U = a 0 + a1 X1 + a 2 X 2 +. ..+a n Xn ,
где a 0 , a1 , a 2 , ... , a n – коэффициенты уравнения регрессии, X1 , X2 , . .. , Xn – объяс-
няющие переменные.
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
41 |
Вектор Х считается отнесённым к реализации W1 (например, наличие явления)
при U≥0, и к реализации W2 (например, отсутствие явления) при U<0. Задача, таким образом, сводится к определению коэффициентов a 0 , a1 , a 2 , . . . , a n , минимизирующих вероятность ошибочной классификации с использованием метода наименьших квадратов.
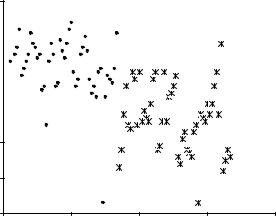
В случае двух объясняющих переменных разделение на классы может быть представлено графически (рис. 17.12, 17.13), что очень наглядно демонстрирует прогностические возможности выбранных предикторов.
Нередко оценка полученных уравнений показывает, что одни уравнения более целесообразно использовать для прогноза класса наличия явления, другие – для класса его отсутствия.
Повышение качества прогнозов на основе линейного дискриминантного анализа может быть достигнуто, если для разделения синоптических ситуаций использовать одновременно две дискриминантные функции и альтернативные прогнозы давать с учетом сочетания знаков этих функций.
Тогда если две схемы (или более) указывают на наличие или отсутствие явления, прогнозировать тот или иной класс можно с большей уверенностью.
Величина B
60
50 

40 
30 
20
10
0
0 |
30 |
60 |
90 |
120 |
Величина A
17.12.Связь метеорологических параметров А и B при наличии (точки)
иотсутствии (звездочки) явления (разделение хорошее)
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
42 |
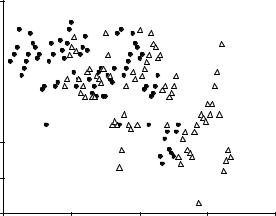
Величина Д
60
50 

40 
30 
20
10
0
0 |
30 |
60 |
90 |
120 |
Величина C
Рис. 17.13. Связь метеорологических параметров С и Д при наличии (точки) и отсутствии (треугольники) явления (разделение неудовлетворительное)
Для уточнения величины прогнозируемого явления применяется приём сочетания дискриминантного и регрессионного анализов. После использования решающего правила, позволяющего отнести синоптическую ситуацию к тому или иному классу, рассчитывается ожидаемая величина явления (например, сильного ветра) с помощью уравнений множественной линейной регрессии, которые строятся отдельно для выборок наличия или отсутствия явления. В случае сложных синоптических ситуаций, когда вероятность осуществления классов близка, ожидаемая величина явления рассчитывается по общей выборке без разделения ситуаций.
17.10. Концепции применения статистических методов для построения способов прогноза погоды
Современные методы статистического анализа и прогноза погоды и опасных ее явлений допускают применение двух концепций - использования статистик "идеального" прогноза (Perfect Prognos Methods – PP) и прогнозов конкретных гидродинамиче-
ских моделей (Model Output Statistics Methods – MOS).
Данные концепции идентичны по используемому статистическому аппарату и различаются способами формирования обучающих выборок.
iКонцепция РР предполагает получение устойчивых оценок диагностиче-
ских (синхронных и асинхронных) связей между рассматриваемыми эле-
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
43 |
ментами или явлениями погоды и значениями ряда характеристик атмосферы, определяемым по фактическим данным на архивном материале.
Выявленные диагностические соотношения, например, в виде уравнений регрессии, переносятся на связи между элементами погоды и прогностическими переменными, которые снимаются с прогностических карт, построенных с помощью той или иной гидродинамической модели.
Неоспоримы достоинства РР-концепции:
•Уравнения регрессии строятся на основе архивных данных за большой период метеорологических наблюдений;
•Качество прогнозов элементов и явлений погоды автоматически повышается при улучшении качества используемых гидродинамических моделей;
•Не требуется пересчета уравнений регрессии при внедрении в практику новой гидродинамической модели.
При применении концепции РР для отбора предикторов используется сравнительно большая географическая область вокруг пункта, для которого составляются прогностические уравнения регрессии.
Недостатки PP-концепции:
•Основным методическим недостатком РР-концепции является то, что в ней не учитываются ошибки конкретной гидродинамической модели, из которой при оперативном использовании берутся значения предикторов. Уравнения регрессии построены на фактическом материале (идеальный прогноз), а при оперативном использовании полученные связи в «чистом» виде переносятся на прогностические поля, из которых выбираются необходимые предикторы для прогноза метеорологических величин и явлений погоды. При этом мы допускаем, что прогностические поля отражают те же особенности пространственно-временного распределения метеорологических величин и условий циркуляции, что и фактические. На самом деле прогностические модели, лежащие в основе прогноза полей метеорологических величин, не могут учесть всего разнообразия процессов, их формирующих.
Этот процесс можно сравнить с процессом разработки дизайнером модели нарядного платья из тонкого шелка, а на практике модель сошьют по той же выкройке, но из грубой льняной ткани – модель одна и та же, но конечный результат будет отличным от модельного, разработанного автором.
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
44 |
По мере совершенствования гидродинамических моделей прогностические поля всё более приближаются к фактическим, но всё же между ними остаются более или менее существенные различия.
Поэтому для уменьшения методической ошибки в уравнения регрессии можно ввести коэффициенты, учитывающие несоответствие прогностических и фактических полей метеорологических величин.
Второй путь – это использование для построения прогностических моделей концепции MOS.
iКонцепция MOS предполагает отбор предикторов и построение уравне-
ний регрессии непосредственно для связей между фактически наблюдавшимися явлениями погоды и прогностическими значениями параметров атмосферы из конкретной гидродинамической модели.
Достоинства MOS-концепции:
•При оперативном использовании построенные уравнения регрессии применяются в сочетании с теми же гидродинамическими моделями, на которых производилось обучение.
Здесь исключается замеченный выше методический недостаток РР-концепции. Уравнения регрессии, построенные в соответствии с MOS-концепцией, действительно наилучшим образом используют прогностическую способность конкретных гидродинамических моделей.
Вэтом основное достоинство MOS-концепции по сравнению с РР-концепцией, которое останется решающим до тех пор, пока гидродинамические прогнозы не станут практически достоверными.
•Качество прогнозов на основе концепции MOS тем выше, чем выше качество прогностических моделей, чем больше полнота и разнообразие получаемых из моделей метеорологических величин и явлений погоды и чем больше архивы прогностических гидродинамических полей, что позволяет построить зависимости для различных пунктов прогнозирования и для разных сезонов года.
Недостатками MOS-концепции являются:
•Качество прогнозов каждый раз ухудшается, когда в гидродинамические модели происходят перестройки, в том числе, и улучшающие модель. Следовательно, для
Н.А. Дашко Курс лекций по синоптической метеорологии
