
- •Нина Александровна Дашко
- •Часть 1
- •1. ВВЕДЕНИЕ
- •1.1. Состав и строение атмосферы
- •1.2. История развития метеорологии как физической науки
- •1.2.1. Древнегреческий период развития науки
- •1.2.2. Эллинистический период развития науки
- •1.2.3. Простонародная метеорология
- •1.2.4. Развитие науки на Востоке
- •1.2.5. Развитие научных связей Европы и Востока
- •1.2.6. Изобретение метеорологических приборов
- •1.2.6. Научные общества и академии
- •1.3. Развитие синоптической метеорологии
- •1.4. ВМО – Всемирная метеорологическая организация
- •1.5. Гидрометеорологическая служба России
- •2. МЕТЕОРОЛОГИЧЕСКАЯ ИНФОРМАЦИЯ
- •2.1. Требования к гидрометеорологической информации
- •2.2. Виды гидрометеорологической продукции
- •2.3. Потребители гидрометеорологической информации:
- •2.4. Кодирование гидрометеорологической информации
- •2.4.1. Структура кода КН-01
- •Схема кода КН-01:
- •Раздел 0
- •Раздел 1
- •Раздел 2 – для судовых или буйковых станций
- •Раздел 3
- •Раздел 4
- •Раздел 5
- •Раздел 0
- •Для сухопутных станций:
- •Передача судовых данных:
- •Раздел 1 (для станций любого типа)
- •Раздел 2 (используется при передаче судовых данных)
- •Раздел 3
- •Раздел 4 (для высокогорных станций)
- •Раздел 5
- •2.4.2. Структура кода КН-04
- •ЧАСТЬ "A" КОДА КН-04
- •ЧАСТЬ "B" КОДА КН-04
- •Особые точки по температуре воздуха:
- •Особые точки по ветру:
- •3. СОСТАВЛЕНИЕ КАРТ ПОГОДЫ
- •3.1. Виды карт погоды
- •3.2. Приземные карты погоды (составление и чтение)
- •Раздел 1
- •Раздел 2
- •Раздел 3
- •3.3. Составление высотных карт погоды
- •3.3.1. Геопотенциал
- •3.3.2. Барометрическая формула геопотенциала
- •3.3.3. Барометрическая ступень
- •3.3.4. Карты барической топографии
- •3.4. Составление вспомогательных карт погоды
- •4. АНАЛИЗ КАРТ ПОГОДЫ
- •4.1. Первичный анализ приземных карт погоды
- •4.1.1. Правила оформления приземной карты погоды
- •4.1.2. Проведение атмосферных фронтов на картах погоды
- •4.2. Первичный анализ высотных карт погоды
- •4.2.1.Правила оформления высотных карт погоды
- •4.2.3. Анализ карт относительной топографии
- •4.3. Анализ вспомогательных карт погоды
- •5. АЭРОЛОГИЧЕСКИЕ ДИАГРАММЫ И ВЕРТИКАЛЬНЫЕ РАЗРЕЗЫ АТМОСФЕРЫ
- •5.1. Аэрологические диаграммы
- •5.1.2. Построение аэрологической диаграммы
- •5.1.3. Анализ аэрологической диаграммы
- •5.1.4. Графические расчёты с помощью аэрологических диаграмм
- •5.2. Вертикальные разрезы атмосферы
- •5.2.1. Правила построения вертикальных разрезов атмосферы
- •5.2.2. Анализ вертикальных разрезов атмосферы
- •5.2.3. Временные разрезы атмосферы
- •Температура воздуха, °С
- •6. ОШИБОЧНЫЕ ДАННЫЕ НА КАРТАХ ПОГОДЫ
- •7. ПРИНЦИПЫ СИНОПТИЧЕСКОГО АНАЛИЗА
- •7.1. Основные синоптические объекты
- •7.2. Информативность карт барической топографии
- •7.4. Обзор синоптического положения за предыдущие сутки
- •8.1. Вычисление производных
- •8.2.1. Прямолинейная интерполяция
- •8.2.2. Криволинейная интерполяция
- •8.2.3. Формальная экстраполяция
- •8.3.1. Траектории воздушных частиц
- •Способ обратного переноса:
- •Рис. 8.4. Способ обратного переноса
- •Способ прямого переноса:
- •8.3.2. Линии тока воздушных частиц
- •9. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОЛЕЙ МЕТЕОРОЛОГИЧЕСКИХ ВЕЛИЧИН
- •9.1.1. Градиент метеорологической величины
- •9.2. Поле атмосферного давления
- •9.2.3. Локальные изменения давления
- •9.3. Динамические изменения давления воздуха
- •9.4. Распределение атмосферного давления на Земном шаре
- •9.5. Поле ветра
- •Цилиндрическая система координат
- •Сферическая система координат
- •Натуральная система координат
- •9.5.2. Силы, действующие в атмосфере
- •Сила барического градиента
- •Отклоняющая сила вращения Земли
- •Сила трения
- •Центробежная сила
- •9.6. Уравнения движения
- •9.6.1. Геострофический ветер
- •9.6.3. Градиентный ветер
- •9.6.4. Действительный ветер
- •9.7. Особенности ветрового режима над Японским морем
- •9.8. Особенности ветрового режима над Охотским морем
- •9.9. Дивергенция и вихрь скорости
- •9.9.1 Дивергенция вектора скорости ветра
- •9.9.2. Вихрь вектора скорости ветра
- •9.9.3. Уравнение тенденции вихря скорости
- •Характерные синоптические масштабы:
- •9.9.5. Уравнение дивергенции скорости
- •9.10. Поле вертикальных движений атмосферы
- •9.10.1. Классификация вертикальных движений атмосферы
- •9.10.2. Упорядоченные вертикальные движения атмосферы
- •9.10.3. Расчёт вертикальных движений атмосферы
- •9.11. Поле температуры воздуха
- •9.11.1. Температурные градиенты
- •9.11.2. Адиабатические изменения температуры воздуха
- •9.11.3. Термический ветер
- •9.11.4. Локальные изменения температуры воздуха
- •10. ВОЗДУШНЫЕ МАССЫ
- •10.1. Масштабы воздушных масс
- •10.2. Очаги формирования воздушных масс
- •10.3. Географическая классификация воздушных масс
- •10.5. Трансформация воздушных масс
- •10.6. Термодинамическая классификация воздушных масс
- •10.7. Характеристики устойчивых воздушных масс
- •10.7.1. Тёплая устойчивая воздушная масса
- •10.7.2. Холодная устойчивая воздушная масса
- •10.8. Характеристики неустойчивых воздушных масс
- •10.8.1. Тёплая неустойчивая воздушная масса
- •10.8.2. Холодная неустойчивая воздушная масса
- •10.9. Оценка устойчивости воздушных масс
- •11. АТМОСФЕРНЫЕ ФРОНТЫ
- •11.1. Ориентация и размеры фронтальной поверхности
- •11.2. Классификация фронтов
- •11.2.1. Географическая классификация атмосферных фронтов
- •11.3. Перемещение фронтов
- •11.4. Профиль движущегося фронта
- •11.5. Общие характеристики фронтов
- •11.5.1. Фронты в барическом поле
- •11.5.2. Фронты в поле ветра
- •11.5.3. Фронты в поле барических тенденций
- •11.5.4. Фронты в поле температуры воздуха
- •11.5.5. Фронты в поле влажности и облачности
- •11.6. Тёплый фронт
- •11.7. Холодный фронт
- •11.7.1. Холодные фронты 1-го рода
- •11.7.2. Холодные фронты 2-го рода
- •11.7.3. Вторичные холодные фронты
- •11.8. Фронты окклюзии
- •11.8.1. Облака и осадки холодного фронта окклюзии
- •11.8.2. Облака и осадки тёплого фронта окклюзии
- •11.10. Образование и размывание атмосферных фронтов
- •11.10.3. Оценка тропосферного фронтогенеза и фронтолиза
- •11.10.4. Приземный фронтогенез и фронтолиз
- •12. ЦИКЛОНЫ И АНТИЦИКЛОНЫ УМЕРЕННЫХ ШИРОТ
- •12.1. Основные определения
- •12.1.1. Вертикальная протяжённость барических образований
- •12.1.2. Оси барических образований
- •12.1.3. Фронтальные и нефронтальные барические образования
- •Модель циклона по Ли
- •Модель циклона по Бьеркнесу и Сульбергу
- •Основные теории возникновения циклонов
- •Конвекционная теория циклонов
- •Механическая теория циклонов
- •Волновая теория циклонов
- •Дивергентная теория циклонов
- •12.2. Условия возникновения барических образований
- •12.3. Стадии развития циклонов
- •12.3.1. Начальная стадия развития циклона
- •12.3.2. Стадия молодого циклона
- •12.3.3. Стадия максимального развития циклона
- •12.3.4. Стадия окклюдирования циклона
- •12.3.5. След циклона
- •12.3.6. Серии циклонов
- •12.4. Стадии развития антициклонов
- •12.4.1. Начальная стадия развития антициклона
- •12.4.2. Стадия молодого антициклона
- •12.4.3. Стадия максимального развития антициклона
- •12.4.4. Стадия разрушения антициклона
- •12.5. Регенерация барических образований
- •12.5.1. Регенерация циклонов
- •12.5.2. Регенерация антициклонов
- •12.6. Перемещение барических образований
- •12.7. Центры действия атмосферы
- •Постоянные центры действия атмосферы:
- •Сезонные центры действия атмосферы:
- •12.7.1. Характеристика ЦДА Северо-Атлантического региона
- •Азорский антициклон
- •Исландская океаническая депрессия
- •12.7.2. Характеристика ЦДА Северной Америки
- •Канадский максимум
- •Калифорнийский минимум
- •12.7.3. Характеристика ЦДА Азиатско-Тихоокеанского региона
- •Азиатский антициклон
- •Алеутский минимум
- •Южноазиатская депрессия
- •Северотихоокеанский антициклон
- •Переходные зоны между центрами действия атмосферы
- •12.7.4. Летние синоптические процессы над Охотским морем
- •12.8. Погода в циклонах на разных стадиях развития
- •12.8.1. Погода в передней части молодого циклона
- •12.8.2. Погода в тёплом секторе молодого циклона
- •12.8.3. Погода в тыловой части молодого циклона
- •12.8.4. Погода в окклюдированном циклоне
- •12.9. Погода в антициклонах
- •12.9.1. Инверсии в антициклонах
- •12.9.2. Фронты в антициклоне
- •12.9.3. Погода в антициклоне
- •13. ВЛИЯНИЕ ОРОГРАФИИ НА АТМОСФЕРНЫЕ ПРОЦЕССЫ
- •13.1. Горные ветры
- •Бора
- •13.2. Облакообразование и осадки
- •13.3. Влияние орографии на атмосферные фронты
- •14. СТРУЙНЫЕ ТЕЧЕНИЯ
- •15. ПРОГНОЗ СИНОПТИЧЕСКОГО ПОЛОЖЕНИЯ
- •15.3. Прогноз эволюции барических образований
- •15.4. Прогноз возникновения новых барических образований
- •15.5. Прогноз перемещения и эволюции атмосферных фронтов
- •15.6. Расчёт давления в точках поля
- •15.6.1. Адвективный способ расчёта давления в точках поля
- •15.7. Оценка приземной прогностической карты
- •16.1. О прогнозе погоды в США и Японии
- •16.1.1. Служба погоды в США
- •16.1.2. Служба погоды в Японии
- •Примечание 1
- •Примечание 2
- •Примечание 3
- •17.1. Критерии определения объёма выборки
- •17.2. Определение свойств выборки
- •17.3. Законы распределения метеорологических величин
- •17.3.2. Нормальный закон распределения
- •17.4. Точность и достоверность оценок выборки
- •17.5. Анализ статистических характеристик
- •17.5.1. Исследование трендовой составляющей
- •17.5.3. Процентили
- •17.5.4. Приёмы аппроксимации
- •17.6.1. Выбор предикторов
- •17.6.2. Формирование обучающей выборки
- •17.6.3. Корреляционный анализ
- •17.6.5. Отбор информативных предикторов
- •17.7.1. Оценки свойств уравнений регрессии
- •17.7.2. Применение пошаговой процедуры расчета
- •17.7.3. Процедура отбора оптимальных уравнений
- •17.11. Статистическая оценка прогнозов
- •17.11.1. Количественные прогнозы
- •17.11.2. Альтернативные прогнозы
- •18.1. Прогноз температуры воздуха у поверхности Земли
- •18.1.1. Адвективные изменения температуры воздуха
- •18.1.2. Трансформационные изменения температуры воздуха
- •18.1.3. Суточный ход температуры воздуха
- •18.2. Прогноз влажности воздуха у поверхности Земли
- •СОДЕРЖАНИЕ
- •АТМОСФЕРНЫЕ ФРОНТЫ
- •СТРУЙНЫЕ ТЕЧЕНИЯ

17. Математическая статистика в синоптической метеорологии |
9 |
дисперсию, а среднее квадратическое отклонение σ, вычисляемое как корень квадрат-
ный из дисперсии:
σ = µ2 = D = |
∑i (xi − ξ)2pi . |
||||
•Третий центральный момент служит в качестве характеристики асимметрии |
|||||
распределения: |
|
|
|
|
|
µ3 = ∑i (xi − ξ)3pi . |
|
||||
Чтобы получить безразмерную величину, вместо µ3 вводят коэффициент асим- |
|||||
метрии: |
|
|
|
|
|
As = |
µ |
2 = |
∑ |
(xi − ξ)2pi |
. |
|
i |
σ3 |
|||
|
σ3 |
|
|
||
iАсимметрия характеризует неодинаковую повторяемость метеорологиче-
ской величины относительно среднего значения или неодинаковость промежутков времени, в течение которых данная метеорологическая величина имеет значения выше средней или ниже средней
•Четвёртый центральный момент используется для оценки крутости кривой распределения по сравнению с нормальной кривой распределения. В качестве меры крутости используют коэффициент эксцесса
E= µ4 = ∑i(xi − ξ)4 pi .
σ4 σ4
iЭксцесс характеризует островершинность (крутость, "пикообразность")
распределения
17.3.2. Нормальный закон распределения
Одним из многих типов распределений, имеющихся в Природе, является нормальный закон, впервые рассмотренный А. Муавром в 1733 г. и в 1809-1812 гг. снова открытый и независимо изученный К. Гауссом и П. Лапласом.
Случайная величина называется распределённой нормально, если она имеет плотность распределения следующего вида:
f (x) = |
[ |
σ |
2π |
] |
−1 |
|
− |
1 |
[x − M(x)] |
2 |
|
, |
|
|
2 |
|
|
||||||||
|
|
|
exp |
|
|
D |
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
10 |
где -∞<x<∞, f (х) – плотность распределения вероятности, а оценки распределения M(x) и D есть
+∞ |
+∞ |
[x − M(x)]2 f (x)dx – |
M(x) = ∫ x f (x)dx, |
D = ∫ |
|
−∞ |
−∞ |
|
математическое ожидание и дисперсия случайной величины (в случае стандартного нормального распределения равны, соответственно 0 и 1).
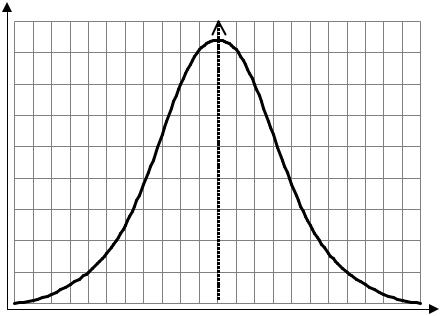
Данная функция имеет вид колоколообразной кривой (рис. 17.2), параметр М(х)
– точка максимума, проходящая через ось симметрии, параметр σ характеризует рас-
стояние от оси Y до точки перегиба. Если σ мало, то кривая распределения заостренная и высокая, если σ велико – широкая и плоская.
Y |
Ось симметрии |
X |
Рис. 17.2. Кривая нормального распределения |
У симметричного распределения асимметрия равна 0. Если асимметрия существенно отличается от 0, то распределение асимметрично.
Если плотность распределения имеет правый «хвост» (в вариационном ряду преобладают варианты, большие среднего значения), то As>0 – правосторонняя асимметрия, если левый «хвост» – As<0 – левосторонняя асимметрия (в вариационном ряду
Н.А. Дашко Курс лекций по синоптической метеорологии
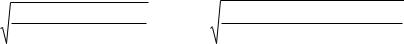
17. Математическая статистика в синоптической метеорологии |
11 |
преобладают варианты, меньшие среднего значения). При правосторонней (левосторонней) асимметрии правая ветвь (левая ветвь) распределения длиннее левой (правой).
Например, если рассмотреть ход температуры воздуха для континентального и морского климата, то окажется, что в морском климате температура воздуха дольше остаётся ниже среднего значения (больше значений ниже среднего, отрицательная асимметрия), а в континентальном – выше среднего значения (больше значений выше среднего – положительная асимметрия).
Эмпирический коэффициент асимметрии не имеет ни верхней, ни нижней границ, что снижает его ценность как меры асимметрии, но при умеренно асимметричных рядах он меньше единицы.
Под эмпирическим эксцессом, или коэффициентом крутости Е понимают обычно уменьшенное на три единицы отношение центрального момента четвёртого порядка к среднему квадратическому отклонению в четвёртой степени. За стандартное значение Е принимают нуль-Эксцесс нормальной кривой распределения.
Кривые, у которых более плоская вершина по сравнению с нормальным распределением, характеризуются отрицательным эксцессом (Е<0) – плосковершинные распределения, а кривые с положительным эксцессом (Е>0) – более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются островершинными.
Иногда распределение может иметь 2 или более пиков.
iАсимметрия и эксцесс показывают степень отклонения эмпирического
распределения от нормального (симметричного)
Коэффициенты асимметрии и эксцесса связаны условиями: As<3 σAs , E>5 σE ,
где σAs и σE – средние квадратические коэффициенты асимметрии и эксцесса:
σAs = |
6n(n − 1) |
, |
σE = |
24(n − 1) |
2 |
. |
|
(n − 2)(n + 1)(n + 3) |
(n − 3)(n − 2)(n + 3)(n + 5) |
||||||
|
|
|
|
||||
Наряду с данными характеристиками в качестве описательных критериев вариационного ряда применяют понятия медианы (Ме) и моды (Мо) распределения. Для медианного значения справедливо равенство
P(x≤Me)=P(x≥Me).
С геометрической точки зрения медиана – абцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
Н.А. Дашко Курс лекций по синоптической метеорологии

17. Математическая статистика в синоптической метеорологии |
12 |
Модальным значением является значение Х, при котором плотность распределения имеет максимум. Бывают одномодальные, двух-, трех- и многомодальные распределения. Другими словами, мода – это значение метеорологической величины, которое наблюдается наибольшее число раз. Нахождение моды не требует каких-либо вычислений – им является вариант, которому соответствует наибольшая частота.
iДля нормального распределения имеет место равенство математического
ожидания, медианы и моды
Таким образом, сопоставляя статистические характеристики выборки, можно судить о близости закона распределения метеорологической величины к нормальному, определить крутость и скошенность распределения.
Термин «нормальный закон распределения» (синоним: распределение Гаусса), получил свое название в силу своей распространённости. Термин «нормальный» т.е. обычный (Normal) применяется в условном смысле, как общепринятый, не означая, однако, что подчинение другим законам распределения выражает какую-то анормальность данной величины или явления.
С точки зрения математической изученности и простоты свойств нормальный закон распределения во многих своих чертах привлекателен и удобен при практическом использовании, особенно в случаях, когда значения тех или иных величин формируются под воздействием большого числа взаимно независимых факторов. Это в полной мере относится ко многим основным метеорологическим величинам и явлениям погоды.
Главной особенностью нормального закона распределения является то, что он является некоторым предельным, к которому приближаются другие распределения.
Кроме нормального закона распределения, в метеорологической практике широко используются и другие типы распределений.
17.4. Точность и достоверность оценок выборки
По имеющейся выборке из генеральной совокупности можно лишь приближённо оценить математическое ожидание М(х), рассчитав выборочное среднее значение
x = ∑xipi , (где х1, х2,..., хi – значения метеорологической величины, р1, р2,..., рi – со-
i
ответствующие им вероятности, i = 1, 2, 3,..., n – число членов выборки).
Н.А. Дашко Курс лекций по синоптической метеорологии
17. Математическая статистика в синоптической метеорологии |
13 |
Средняя величина, вычисленная по элементам другой выборки того же объёма и из той же генеральной совокупности, определяется числом, как правило, отличным от первого, т.е. среднее может изменяться от выборки к выборке.
Оценивая выборочные средние величины какого-либо ряда наблюдений, мы оцениваем параметры генеральной совокупности, т.е. по ( x ) пытаемся оценить М(х). Но выборочная средняя величина является точечной оценкой конкретного ряда и не определяют точность и достоверность оценки выборки.
Достоверность и точность могут быть получены путем определения доверительных (конфиденциальных) оценок (границ), характеризуемых шириной доверительного интервала и доверительной вероятностью. Доверительный интервал является мерой точности оценивания параметра, доверительная вероятность характеризует степень достоверности или надежности результатов.
Чтобы судить об М(х) по x , необходимо найти доверительный интервал, в котором лежит истинное среднее М(х), с заданной доверительной вероятностью
P[a ≤ M(x) ≤ b]= 1 − α ,
или
P x − M(x) ≤ β = 1 − α .
Здесь α – вероятность ошибки (0.05, 0.01 или в процентах, соответственно 5%, 1% и т.д.) или уровень значимости, a и b – доверительные (конфиденциальные) грани-
цы, β – доверительный (конфиденциальный) интервал.
Доверительные границы a и b ограничивают с некоторой вероятностью (например, 95%, 99% и т.д.) область, в которой лежит истинное среднее (неизвестный параметр). Вероятность того, что неизвестный параметр окажется внутри построенного ин-
тервала β, и называют доверительной вероятностью 1-α.
В каждом конкретном случае выбор значения (1-α) зависит от вида решаемой задачи. Если мы выбираем 1-α=0.95 (или α=0.05), это означает, что в 95 случаях из 100
истинное значение параметра лежит внутри данного интервала. С возрастанием 1-α до-
верительный интервал становится все длиннее, оценивание, следовательно, – все неопределеннее.
Из теории статистики известно, что для оценки математического ожидания М(х) по значению выборочного среднего можно использовать равенство
Н.А. Дашко Курс лекций по синоптической метеорологии

17. Математическая статистика в синоптической метеорологии |
|
|
|
|
14 |
||
|
|
P[a ≤ M(x) ≤ b]= 1 − α , |
|
|
|
||
преобразованное к виду: |
|
|
|
|
|
|
|
|
P |
(x − tp σ ) ≤ M(x) ≤ (x + tp |
σ |
) |
= 1 − α . |
|
|
|
|
n |
n |
|
|
|
|
Здесь tp – |
статистика распределения |
|
Стьюдента, a = (x − tp |
σn ) , |
|||
b = (x + tp |
σn ) . |
|
|
|
|
|
|
Процедура определения доверительного интервала:
1.Выбрать доверительную вероятность 1 − α и определить соответствую-
щее число tp из таблицы стандартного нормального распределения;
2.Вычислить параметр выборки, например, x , а также доверительные границы a и b;
3.Задать доверительный интервал для истинного параметра:
|
|
|
P[a ≤ M(x) ≤ b]= 1 − α . |
|
|
|
Наиболее употребительными значениями tp |
для выборки с числом членов 100 и |
|||||
более являются следующие: |
|
|
|
|
||
|
1 − α |
0.90 |
0.95 |
0.99 |
0.999 |
|
|
|
|
|
|
|
|
|
tp |
1.645 |
1.960 |
2.576 |
3.291 |
|
Если необходимо определить интервал для выборки при n≥100, в котором лежит
истинное значение М(х) с вероятностью Р=0.95 (95%), используют табличное значение t0.95=1.96, с вероятностью Р=0.99 (99%) – t0.99=2.576.
Для нормального распределения случайной величины имеют место следующие
соотношения: |
|
|||||
P[(x |
|
|
|
+ σ)]= 0.68 |
(68%) |
|
− σ) ≤ xi ≤ (x |
||||||
P[(x |
|
|
+ 2σ)]= 0.95 |
(95%) |
||
− 2σ) ≤ xi ≤ (x |
||||||
P[(x |
|
|
+ 3σ)]= 0.97 |
(97%). |
||
− 3σ) ≤ xi ≤ (x |
||||||
Следовательно, около 68% всех возможных значений случайной величины хi
лежит в пределах (x ± σ) , около 95% – в пределах (x ± 2σ) , и практически рассеяние случайной величины хi заключено на участке (x ± 3σ) . Это правило называется «пра-
Н.А. Дашко Курс лекций по синоптической метеорологии

17. Математическая статистика в синоптической метеорологии |
15 |
вилом трех сигм». Таким образом, вероятность того, что нормально распределённая случайная величина хi не попадает в этот участок, составляет всего 3 случая из 1000.
В заключение отметим, что при симметричном распределении – α1 = α2 = α / 2 ,
|
σ |
σ |
|
или |
(x − tp n ) = (x + tp |
n ) , при асимметричном – доверительные интервалы справа |
|
|
|
σ |
σ |
и слева от истинного среднего различаются, т.е. (x − tp n ) ≠ (x + tp |
n ) . |
||
Статистические приёмы позволяют получить представление о достаточной длине выборки из генеральной совокупности, используемой для получения, например, выборочных средних величин заданной точности, которые в дальнейшем при увеличении длины ряда не претерпевают заслуживающих внимания изменений для статистически стационарных процессов.
Если обозначить tpnσ = ∆ , то по заданной точности ∆ и найденному значению
tp , всегда можно вычислить объём выборки n:
tp2σ2 = ∆n , откуда n = (tp2σ2 ) ∆2 .
∆2 .
Например, если требуемая точность ∆ оценки средней месячной температуры воздуха (половина доверительного интервала) составляет 0.5°С, доверительная вероят-
ность 1 − α =0.95 (95%), то при дисперсии σ2 =5 (°С)2 объём выборки должен составить не менее 77 лет. При дисперсии средней суточной температуры, равной 16 (°С)2 и точности выборочного среднего от 0.1 °С до 1 °С объём необходимой выборки для вычисления средней месячной температуры воздуха изменяется от 6144 до 60 случаев, т.е. от
200 до 2 лет.
Поскольку для точности оценки выборочного среднего для суточных оценок, равной 0.1-0.2 объём требуемой достоверной выборки слишком велик по сравнению с имеющимися возможностями, его необходимо снизить, например, путем увеличения доверительного интервала. Кроме того, следует учитывать остаточную неоднородность метеорологических рядов, за счёт которой вносится определенная погрешность в среднее значение и которую не удается устранить При точности оценки 0.4-0.6 длина выборки может ограничиваться периодом от 13 до 6 лет.
Зависимость требуемого объёма выборки от величины дисперсии выборочного среднего приводит к различию её объёма для отдельных месяцев. Чем меньше диспер-
Н.А. Дашко Курс лекций по синоптической метеорологии
