Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

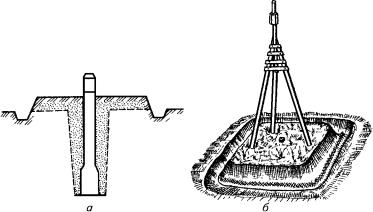
са. В их нижнюю часть вставляют поперечные штыри, предо-

храняющие знак от вытаскивания из земли. Реже применяют деревянные столбы, так как они не обеспечивают нужной сохранности.

При больших расстояниях между точками (несколько км) их

обозначают деревянными или металлическими сооружениями — пирамидами (ðèñ. 1.21, á), или более сложными сооруже-

ниями — сигналами. Для обеспечения долговечности знака (пункта) под пирамидами и сигналами закладывают так назыв˝а-

åìûå центры, состоящие из железобетонных монолитов, ниж-

ний из которых закладывают на глубину 2,2 м. Чтобы измерить угол, надо осторожно раскопать насыпь до марки верхнего м˝о- нолита, находящейся на глубине до 0,5 м, над ней поставить уг˝-

ломерный прибор. После окончания измерений насыпь восста˝-

навливают.

Измерение состоит в сравнении значения измеряемого угла или

длины измеряемой линии с принятой единицей измерения — ˝угловым градусом, метром и др. Например, при измерении линии

определяют, сколько раз метровый отрезок укладывается в длине этой линии. Измеряют углы на местности угломерными прибо-˝

рами, в основном теодолитами, а линии — различными приборами, от самых простых (рулетки, ленты, проволоки) до сложных

(оптические è электромагнитные дальномеры). Числовые значе- ния, получаемые в процессе измерений, записывают в специа˝ль-

ные полевые журналы и абрисы (схематические чертежи) или

фиксируют в накопителях информации электронных измерительных приборов.

При выполнении полевых (на местности) и камеральных (â ëà-

бораторных помещениях) вычислительных и графических раб˝от

Рис. 1.21. Закрепление точек местности межевым знаком (à) и пирамидой (á)

51

самое серьезное внимание обращают на аккуратность и четк˝ость

вычерчивания и записей.

Полевые журналы и абрисы заполняют и вычерчивают четко, с˝ таким числом пояснительных надписей, чтобы любой специал˝ист без затруднений мог производить последующую вычислител˝ьную

обработку полевых измерений и составление планов. Все пол˝евые данные записывают хорошо отточенным карандашом средней˝

твердости, а в практике некоторых учреждений даже тушью. П˝од- чистки, записывание одной цифры по другой и обводы полевы˝х

записей не допускаются. Неправильно записанное число акк˝урат-

но зачеркивают одной линией и над ним пишут правильное чи˝сло (подчистку и аккуратное исправление цифр допускают лишь ˝при выполнении камеральных вычислительных работ).

Если результаты повторных измерений записаны на другой

странице журнала или в другом журнале, то возле зачеркнутого результата указывают, на какой странице и в каком номере ж˝урна-

ла даны эти записи.

Испорченные по какой-либо причине страницы журнала не

уничтожают, а по диагонали пишут «испорчено» и указывают ˝номер страницы, где записи продолжаются. Листы или страницы˝

журналов и других документов до работы нумеруют и число л˝истов или страниц заверяют подписью начальника отряда (пар˝тии,

экспедиции). В журналах указывают дату, условия измерений˝ и фамилии исполнителей.

Никакие записи и вычисления в «черновиках» и переписыва-

ние с них не допускаются.

Чертежные работы выполняют на специальной доске или на ровном столе при помощи выверенных линеек, треугольников˝,

измерителей с острыми иглами и пр.

При полевых и камеральных вычислениях записи выполняют

прямым вычислительным шрифтом (рис. 1.22), при котором четные цифры должны выступать вверх, нечетные опускаться вни˝з наполовину высоты строки, единица и нуль остаются на стро˝ке.

Выполняя действия с числами, цифры записывают одну под другой. При сложении и вычитании целые части пишут под цел˝ы- ми, а дробные — под дробными. Многозначные числа пишут группами, по две-три цифры в группе, например 6 958 354,3 или tg 14°47,2′ = 0,26396. Целые части от дробных отделяют запятыми.

При записях результатов измерений или при действиях с чис˝-

лами часто прибегают к целесообразному округлению чисел˝. На-

пример, число π округляют следующим образом: 3,14159; 3,1416;

Рис. 1.22. Вычислительный шрифт

52

3,142; 3,14; 3,1; 3. Если в числе последняя цифра 5, то, округляя

ее, оставляют четную цифру. Например, число 12,825 округляют до 12,82, а 0,575 — до 0,58.

Записывают результаты измерений числом цифр, соответств˝у- ющим точности измерений. Не записывают, например, результ˝ат

измерения угла числом 5°00′, если угол измерен с точностью до 1°, и наоборот, не записывают результат измерения числом 5°, ес˝ли

измерение проводили с точностью до минуты, хотя результат˝ измерения оказался равным 5°00′. Не считают равными по точности

числа, записанные так: 5, 5,0, 5,00 м и т. д. Если линия измерена с

точностью до 0,1 м, то пишут 278,3 м, а не 278,30 м, а если до 0,01 м, то — 278,30 м, а не 278,3 м.

Точность измерений характеризуют погрешностями (ошибками)

измерений. Погрешностью измерения называют разность между

Ее получают по правилу: из того, что имеется, вычитают то, чт˝о должно быть. Точное значение измеряемой величины можно по˝-

лучить, используя прибор более высокой точности. В отдель˝ных случаях точное значение величины известно. Например, точн˝ая

сумма значений измеренных углов в плоском треугольнике р˝авна 180°, а сумма измеренных углов оказалась 179°58,5′, тогда погреш-

ность суммы измеренных углов будет –0°01,5′. Эту погрешность

называют угловой невязкой треугольника.

Но одно значение погрешности , вычисленное по формуле (1.25), не характеризует точность измерения, потому что, повто˝-

ряя измерения величины, будем получать различные значени˝яli.

Поэтому в качестве обобщенной характеристики точности и˝зме-

рений принимают среднюю квадратическую погрешность, вычисляемую по многократным измерениям l1, l2, …, ln, а следовательно, и по 1, 2, …, n, пользуясь формулой Гаусса

= + + + (1.26)

ãäå ï — число измерений.

Погрешности и ò называют абсолютными и пользуются ими для оценки точности измерений, не зависимых от величины l, например от значения угла, т. е. принимают, что углы в 1° и в 100° измеряют в одинаковых условиях, одним и тем же прибором с одинаковой точностью. Погрешности измерений линий, завис˝и- мые от их длины, характеризуют относительными погрешностями, т. е. отношением абсолютной погрешности к результату изме˝рения: /l — относительная погрешность измерения, а m/l — относительная средняя квадратическая погрешность измерения˝.

53

Иногда точность измерений характеризуют расхождением м˝еж-

ду результатами измерений одной и той же величины d = l1 – l2 или относительным расхождением d/l. Например, l1 = 215,73 ì, l2 = 215,84 м, тогда

d/l = (215,73 – 215,84)/216 = –0,11/216 = –1/1960.

Для определения допустимости расхождений или невязок ис˝- пользуют предельные погрешности, которые принимают как удво-

енные или утроенные средние квадратические погрешности˝, т. е.

1.20. ПРАВИЛА ДЕЙСТВИЙ С ПРИБЛИЖЕННЫМИ ЧИСЛАМИ

При геодезических измерениях и вычислениях приходится иметь дело преимущественно с приближенными числами. Напр˝и- мер, результат измерения линии записан с округлением до д˝вух

десятичных знаков или до сотых долей метра — 128,23 м. Это чис˝-

ло неточное, за последней цифрой следует бесконечно больш˝ое число цифр, которые отброшены при их округлении, потому чт˝о

они уже не соответствуют точности измерения. Также число 1,414214, полученное после извлечения квадратного корня из 2, не

является точным, в нем шестым десятичным знаком была цифр˝а 3, седьмым — 5 и т. д., поэтому шестой знак округлен до 4.

Для правильного действия с приближенными числами в них

различают: десятичные знаки, значащие и верные цифры. Десятичными знаками называют все цифры после запятой, значащими — все цифры числа, кроме нулей слева и справа, если

последние при округлении поставлены вместо других цифр. На-

пример, число 4108,207 имеет три десятичных знака и семь зна-

чащих цифр. Число 0,0035 имеет четыре десятичных знака и две

значащие цифры. Если говорят, что в населенном пункте 16 000 жителей, то в этом числе две значащие цифры, так как

нули поставлены вместо других цифр. Но в числе =

пять значащих цифр, потому что в нем нулями не заменены ка- кие-либо цифры.

Каждая цифра или группа цифр в числе имеет название в зави˝- симости от места, которое она занимает в числе среди десят˝ичных знаков или значащих цифр. Например, в числе 4108,207 последняя цифра 7 может быть названа как 7 единиц третьего десяти˝ч- ного знака или 7 единиц седьмой значащей цифры, или 0,7 едини-

цы второго десятичного знака и 0,7 единицы шестой значащей цифры. Группа цифр 82 в этом числе может быть названа как

54

82 единицы первого десятичного знака или 82 единицы пятой зна- чащей цифры и т. д.

Верными называют цифры числа, засуживающие доверия. На-

пример, если результат измерения записан так: 128,23 м, а измер˝е- ние проводили с точностью до 1 м, то в этом числе будут лишь˝ три (128) верные цифры, а последние две цифры неверные, не заслуживающие доверия.

В таком точном числе, как 180°, выражающем сумму углов

плоского треугольника, число верных значащих цифр бескон˝ечно большое. В формуле (1.3) число 2 также имеет бесчисленное мно-

жество верных значащих цифр.

При вычислениях выдерживают такое число значащих цифр,

десятичных знаков, знаков логарифма, которое обеспечивае˝т нужную точность результатов и не загружает вычисления невер˝ными

или ненужными цифрами.

Рассмотрим некоторые действия с числами.

Сложение и вычитание приближенных чисел. Если числа содержат неодинаковое число десятичных знаков, то при их сложе˝нии и

вычитании оставляют столько десятичных знаков, сколько и˝х

имеет приближенное число с наименьшим числом десятичных˝ знаков плюс одна запасная цифра.

Например, при сложении чисел, имеющих верные значащие

цифры: 12,137 54 + 0,27 + 287,6 + 1253,852 число 287,6 имеет наи-

меньшее число десятичных знаков. Остальные числа перед сл˝ожением (вычитанием) надо округлять так: 12,14 + 0,27 + 287,6 +

+ 1253,85 = 1553,9.

Полученный результат (1553,9) содержит все верные значащие

цифры. Если бы мы не округляли остальные числа и вычислени˝я вели до пяти десятичных знаков, приписав вместо неизвестн˝ых

десятичных знаков вопросительные знаки, то, складывая, по˝лучи- ли бы:

12,13754

0,27 ???

287,6? ???

1253,852??

1553,9? ???

Наличие вопросительных знаков на месте второго, третьего˝ и т. д. десятичных знаков свидетельствует о целесообразности проведенного выше округления слагаемых и нецелесообраз˝ности оставления третьего, четвертого и пятого десятичных знак˝ов. Если

нужно иметь сумму с двумя верными десятичными знаками, то˝ число 287,6 нужно уточнить, чтобы оно имело верный второй десятичный знак. Если нужно иметь сумму с тремя десятичными˝

знаками, то число 287,6 должно иметь верные второй и третий де-˝ сятичные знаки, а число 0,27 — верный третий десятичный знак˝.

55

Поэтому сумма или разность приближенных чисел имеет

столько верных десятичных знаков, сколько их имеет число ˝с наименьшим количеством десятичных знаков. Поэтому в слагаем˝ых (уменьшаемых и вычитаемых) в сумме (разности) должно быть одинаковое число десятичных знаков.

Необходимое число десятичных знаков определяется налич˝ием

èв исходных величинах или в результатах измерений.

Умножение и деление приближенных чисел. Если числа содержат

неодинаковое число значащих цифр, то при умножении и деле˝нии

их оставляют столько значащих цифр, сколько их содержит п˝ри-

ближенное число с наименьшим количеством значащих цифр, плюс одна запасная значащая цифра.

Например, при умножении и делении чисел 12 827,53 и 2,13, у

которых все значащие цифры верные, число с наименьшим кол˝и-

чеством значащих цифр будет 2,13. Поэтому перед умножением или делением другое число надо округлить до 12 830. Если это ок˝-

ругление не сделать, а произвести умножение (12 827,53 · 2,13 = = 27 322,6389), то результат будет иметь очень большое число не-

верных цифр. В этом легко убедиться, если к числу с наименьш˝им количеством значащих цифр прибавить еще одну значащую ци˝ф-

ру, т. е., например, принять 2,133, тогда 12 827,53 · 2,133 = = 27 361,12149. В этом результате по сравнению с первым совпали

только три первые цифры, т. е. столько, сколько их было в чис˝ле с наименьшим количеством значащих цифр. Это же можно пока-

зать на примере с вопросительными знаками:

12 827,53 2,13?

???????

3848259

1282753

2565506

273???????,

т. е. в произведении оказались три верные цифры. Поэтому в д˝анном случае необходимо умножение: 12 830 ·2,13 = 27 300 = = 2,73 · 104.

Если нужно иметь в произведении или частном от деления ещ˝е одну верную цифру, то число 2,13 нужно уточнить, чтобы оно имело верную четвертую значащую цифру.

Произведение и частное имеют столько верных значащих

цифр, сколько их в числе с наименьшим количеством значащи˝х цифр. В связи с этим в сомножителях (делимых и делителях) и произведении (частном) должно быть одинаковое число знач˝ащих

öèôð.

Необходимое число значащих цифр определяется наличием и˝х в исходных значениях или в результатах измерений.

56

Возведение в степень и извлечение корня. По аналогии с произ-

ведением при возведении числа в степень в полученном числ˝е надо оставить столько значащих цифр, сколько их было в чис˝ле, возводимом в степень, т. е. 42,272 = 1787.

Если в результате извлечения корня требуется получить че˝тыре

значащие цифры, то в подкоренном числе надо оставить тако˝е

=

Приближенный способ вычислений при малых значениях угло˝в.

Этот способ применяют, когда значения синусов или тангенс˝ов малых углов можно заменить значениями углов, выраженных в˝

радианной мере, представляющей отношение длины дуги, на к˝о-

торую опирается угол, к радиусу дуги, т. е. sin n » nðàä » tg n.

Так как выражение угла в радианной мере пропорционально

градусному значению угла, т. е.

nðàä/p = n°/180°, òî nðàä = n°p/180° = n°/r° = n¢/r¢ = n²/r²,

где p = 3,141 59; r° = 57,295 8° » 57,3°, r¢ = 3437,75¢ » 3438¢, r² = 206 265² — соответственно число градусов, минут и секунд в радиане.

Поэтому для малых углов n применима формула

Этот способ применяют в зависимости от того, с каким колич˝е- ством значащих цифр нужно получить результат вычислений˝. Чем

больше угол, тем больше синус и тангенс будут отличаться о˝т вы-

ражения угла в радианах.

Значения углов, при которых по формуле (1.28) можно полу-

чить синус и тангенс с определенным числом верных значащи˝х

цифр (с точностью до половины единицы последней значащей˝ цифры), приведены в таблице 1.4.

1.4. Некоторые малые углы n и формулы для вычисления sin и tg этих углов

57

ными будут четыре значащие цифры.

1.21. ПОНЯТИЕ О СЪЕМКАХ МЕСТНОСТИ

Все съемочные работы, выполняемые в поле (на земле, под землей, над землей), называют полевыми, а вычислительные и графические, выполняемые в кабинетах и лабораториях, — камеральными.

Для составления карт, планов и профилей местности необход˝и- мо в поле измерить линии и углы. Процесс таких измерений на˝- зывают съемкой местности. Съемку, выполняемую для получе- ния высот точек и превышений между ними, называют нивелированием.

Всякую съемку проводят по основному правилу геодезии — ˝от общего к частному, т. е. сначала определяют положение осно˝вных точек, создают так называемую съемочную геодезическую сеть, а затем проводят съемку ситуации.

Âпроцессе съемки ситуации устанавливают взаимное полож˝е- ние отдельных характерных точек снимаемых объектов. Напр˝и- мер, при съемке строений устанавливают взаимное положени˝е их углов, при съемке канав, дорог определяют взаимное положе˝ние их поворотов, а при съемке пахотных угодий — взаимное пол˝ожение поворотных точек контуров (очертаний) угодий и пр.

Съемки имеют названия в зависимости от назначения или це-˝ лей, для которых их выполняют: сельскохозяйственные, почв˝енные, лесные, городские, геологические и др.

Объектами сельскохозяйственных съемок являются: границы

землепользований и административные границы, населенны˝е

пункты и отдельно стоящие постройки, сельскохозяйственн˝ые

угодья (огороды, пашни, сенокосы, пастбища), леса, кустарник˝и и

отдельно стоящие деревья, полезащитные лесные полосы и ал˝леи,

болота, пески, солонцы, солончаки, такыры, каменистые россы˝-

пи, пути сообщения, воды и водные сооружения, энергосети и

средства связи, рельеф местности.

При почвенных съемках на план или карту наносят нужные дл˝я

изучения почв объекты, почвенные разрезы, прикопки и конт˝уры

почвенных разновидностей.

Âзависимости от применяемых приборов различают следующие виды съемок: теодолитные, мензульные, тахеометрически˝е,

аэрокосмические, фототеодолитные, нивелирные.

Для получения планов небольших участков местности, заним˝а-

ющих площади в несколько сотен и тысяч гектаров, применяю˝т

теодолитные и мензульные съемки. Если на плане или карте т˝ре-

58

буется изобразить рельеф местности, то обычно методом тео˝до-

литной съемки определяют взаимное положение точек съемо˝чной геодезической сети, а ситуацию местности снимают мензуло˝й. Особенность мензульной съемки состоит в том, что план мес˝тности составляют непосредственно в поле в процессе съемки.

Для небольших участков при необходимости изобразить на плане рельеф или создать цифровую модель местности приме˝няют

тахеометрическую съемку. Основной вид съемки для значите˝льных по площади территорий — аэрокосмическая фотосъемка˝, за-

ключающаяся в последовательном фотографировании местно˝сти

при помощи особого автоматического фотоаппарата, устана˝вливаемого на воздушном или космическом носителе. Для изготовл˝е- ния карт, планов или цифровых моделей местности по фотосн˝им-

кам применяют фотограмметрические и стереофотограмметр˝иче-

ские приборы, при этом положение основных точек геодезиче˝с- ких сетей определяют методами теодолитных съемок.

Для горной и всхолмленной местностей применяют фототеод˝о- литную съемку, при которой местность фотографируют при по˝мо-

щи фототеодолита, а затем на специальных приборах по фото˝- снимкам составляют план местности.

Иногда возникает необходимость в быстрой (приближенной)˝ съемке местности. В этом случае применяют полуинструмент˝аль-

ную или глазомерную съемку и барометрическое нивелирова˝ние.

Контрольные вопросы и задания

1. Что называется уровенной поверхностью? 2. Поверхность как˝ой фигуры более всего соответствует поверхности геоида? 3. Что называю˝т проектированием точек земной поверхности, как и на что их проектируют? 4. Что˝ такое горизонтальный угол? 5. Что называют углом наклона? 6. Что называют го˝ризонтальным проложением линии и по каким формулам его вычисляют? 7. Что ˝называют картой, планом, профилем? 8. В чем сущность геодезической съемк˝и? 9. Какие системы координат различают на плоскости? 10. Что такое широта и д˝олгота точки местности? 11. Какие координаты называют прямоугольными и как˝овы их знаки? 12. Что называют масштабом плана? 13. Какие бывают масштабы пла˝нов? 14. Что называют точностью масштаба? 15. Какая точность у масштабов˝ 1:17 000, 1:23 000, 1:45 000? 16. Что называют склонением магнитной стрелки и по какой˝ формуле его вычисляют? 17. По названию какой оси меридиану присвоено˝ название «осевой»? 18. Что называют дирекционным углом линии? 19. Что называ˝ют сближением меридианов и по какой формуле его вычисляют? 20. В чем преи˝мущество использования дирекционных углов по сравнению с азимутами˝? 21. Прямой дирекционный угол линии равен 85°14′. Чему равен обратный дирекционный угол?

59

à ë à â à 2

ТЕОДОЛИТНАЯ СЪЕМКА

2.1. СУЩНОСТЬ ТЕОДОЛИТНОЙ СЪЕМКИ. ПРИМЕНЯЕМЫЕ ПРИБОРЫ

Теодолитная съемка, как и съемки других видов, является по˝-

левой работой, при выполнении которой сначала создают съе˝мо- чную геодезическую сеть (рис. 2.1), а затем производят съемку˝ си-

туации. Основной прибор, с помощью которого выполняют это˝т

вид съемки, — теодолит, предназначенный для измерения гори-

зонтальных углов и углов наклона.

Съемочной геодезической сетью при теодолитной съемке мо˝- жет быть сеть треугольников (рис. 2.1, à), сеть теодолитных поли-

гонов (рис. 2.1, á), составляющих группу смежных многоугольни-

ков, или теодолитных ходов (рис. 2.1, â), представляющих систему

ломаных линий, привязанную к геодезическим пунктам. При

съемке небольших участков съемочная сеть может представ˝лять один полигон или ход. Ход, проложенный внутри полигона для˝

съемки ситуации, называют диагональным (ðèñ. 2.1, á).

Перед производством измерений все вершины (поворотные

точки) полигонов и ходов закрепляют на местности кольями˝,

столбами и пр. После этого измеряют длины сторон (линий) по˝-

лигонов и ходов, горизонтальные углы между ними, углы накл˝она линий для последующего вычисления их горизонтальных про˝ло-

жений.

Таким образом, процесс теодолитной съемки состоит из закрепления точек на местности, измерения линий и углов в по˝лигонах и ходах, съемки ситуации.

Для измерения линий в полигонах и ходах применяют сталь-

ные ленты, рулетки, дальномеры различных видов и другие пр˝и-

боры, позволяющие измерять линии с относительной погрешн˝о- стью не более 1/2000.

Для измерения больших расстояний целесообразно применя˝ть радио- и светодальномеры, обеспечивающие большую точност˝ь измерений.

Углы в теодолитных полигонах и ходах измеряют при помощи

теодолитов со средней квадратической погрешностью не бо˝лее

0,5′.

60