
Материал первого семестра
.pdf
Московский Государственный Университет Геодезии и Картографии
Ка фе др а в ы сш ей м ат е м ат и к и
Высшая математика (1 семестр)
Р а з д е л ы
Функции. Пределы. Дифференцирование. Интегрирование.
|
О сн о в н ы е фо р м ул ы п о т ем ам |
стр. |
|
|
|
1 |
Пределы |
2 |
2 |
Точки разрыва (рисунков пока нет) |
3 |
3 |
Техника дифференцирования |
4 |
4 |
Приложения производной (в том числе, исследование функций) |
5 |
5 |
Первообразные, подведение под знак дифференциала |
6 |
6 |
Некоторые правила и формулы интегрирования (кое-что ещѐ надо вписать) |
7 |
7 |
Приложения интегралов (формулы пока не вписаны) |
7 |
8 |
Неберущиеся интегралы |
8 |
9 |
Некоторые формулы тригонометрии (формулы пока не вписаны) |
8 |
10 |
Касательная, нормаль |
8 |
|
Составитель |
Л и с е е в И. А. |
П о с л е д н е е р е д а к т и р о в а н и е : |
0 7 - 1 0 - 0 9 . |
Ф Э У Т 1 - 1 , 2 , 8 ( о с е н ь 2 0 0 7 ) |
|
|
|
|
Л е к т о р Л и с е е в И . А . |
|||
|
|
1 . П Р Е Д Е Л Ы |
|
|
|
|
||
|
С в о й с т в а л и н е й н о с т и п р е д е л ь н о г о п е р е х о д а . |
|
|
|
|
|||
Предел суммы или разности … равен сумме или разности пределов … |
|
|
|
|
|
|||
Постоянный множитель можно вынести за знак предела. |
|
|
|
|
|
|
||
|
|
П р е д е л п р о и з в е д е н и я и д р о б и |
|
|
|
|
||
Предел произведения равен произведению пределов … |
Предел отношения равен отношению пределов … |
|||||||
|
|
П р е д е л с т е п е н и и к о р н я |
|
|
|
|
||
|
|
l i m a ( x ) |
l i m |
( x ) |
|
|
|
|
l i m ( ( x ) p ) [ l i m ( x ) ] p ; |
a x |
; l i m n |
( x ) n |
l i m ( x ) . |
||||
x |
x |
x |
|
x |
|
|
x |
|
(Знак предела можно вносить под знак непрерывной функции)
– эта формула "работает" при вычислении пределов показательно степен-
ных функций путем сведения их ко второму замечательному пределу.
Т е о р е м а о п р о и з в е д е н и и б е с к о н е ч н о м а л о й в е л и ч и н ы н а о г р а н и ч е н н у ю .
Произведение бесконечно малой величины на ограниченную есть величина бесконечно малая.
Н е к о т о р ы е п р е д е л ы
l i m |
1 |
|
( |
1 |
|
|
) , |
|
l i m |
1 |
|
0 ( |
1 |
|
0 ) |
, |
l i m |
sin x |
|
1 , l i m ( 1 |
1 |
) x e . |
|||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
x 0 x |
0 |
|
|
|
x x |
|
|
|
|
|
|
x 0 |
x |
|
x |
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Другая запись второго замечательного предела |
l i m |
( 1 |
|
1 |
|
) x |
e |
|
|
|
|
|
|
||||||||||||||||
|
x |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Некоторые "неопределѐнности" : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратите внимание, в этих формулах единица и |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
нули – это не константы, |
так обозначены переменные величины, имеющие пределом единицу или ноль. |
|
|
||||||||||||||||||||||||||
П о в е д е н и е н е к о т о р ы х ф у н к ц и й .
С т е п е н н ы е :
y = х р , |
|
п о к а з а т е л ь н ы е : y = a x , |
л о г а р и ф м и ч е с к и е : |
y = l o g a x |
||||||||||
р > 1 |
р = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 < р < 1 |
|
|
|
|
|
|
|
|
a > 1 |
|
|
|
a < 1 |
|
|
|
|
|
a > 1 |
a < 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k > 0 |
|
y |
k |
|
К о р е н ь к в а д р а т н ы й : |
. |
|
|
||||||
|
|
k < 0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
/2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А р к т а н г е н с : y = a r c t g x . |
|
|
|
|
||
Обратно пропорциональные функции |
|
|
|
|
|
- /2 |
||||||||
|
|
|
|
|
|
|||||||||
При стремлении аргумента х |
к бесконечности многочлен P n ( x ) также стремится к бесконечности. |
|||||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О с н о в н о е л о г а р и ф м и ч е с к о е т о ж д е с т в о : |
A = e l n A |
|
|
||||||||
Это тождество, а также свойство непрерывности показательной функции (подведение знака предела под знак показательной функции) используется при вычислении пределов показательно степенных функций:
l i m a( x ) p( x ) l i m e ln a( x ) p( x ) |
|
l i m p( x ) ln a( x ) |
|
|
||
|
l i m e p( x ) ln a( x ) e x |
... |
|
|
||
x |
x |
|
x |
|
|
|
|
Т а б л и ц а э к в и в а л е н т н о с т е й |
|
|
|
||
Переменные величины р ( х ) и ( х ) |
называются эквивалентными при х → |
, если |
|
. |
||
|
||||||
Понятие эквивалентности применяют для сравнения как бесконечно малых величин, так и для сравнения бесконечно больших величин. При вычислении пределов используют следующее практическое правило: предел произведения или отно-
шения каких-то величин не изменится, если эти величины заменять величинами, им эквивалентными.
- 2 -

При стремлении аргумента к бесконечности (при х ) многочлен
Р n ( x ) = a n x n + a n – 1 x n – 1 + a n – 2 x n – 2 + . . . + a 1 x + a 0
эквивалентен своему старшему члену: Р n ( x ) ~ a n x n .
Эта эквивалентность сохраняется, даже когда n – не целое, но положительное.
Ещѐ некоторые примеры эквивалентности бесконечно больших при х :


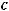

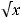 , ℓn (x +c ) ~ ℓn x . Эти эквивалентности всѐ время используются при исследовании рядов на сходимость. Это у нас будет на втором курсе.
, ℓn (x +c ) ~ ℓn x . Эти эквивалентности всѐ время используются при исследовании рядов на сходимость. Это у нас будет на втором курсе.
Эквивалентность некоторых бесконечно малых при стремлении аргумента 0 .
s i n ~ |
|
t g ~ |
|
a r c s i n ~ |
|
a r c t g ~ |
||||||||
1 cos ~ |
|
a 2 |
|
|
e |
– 1 ~ |
|
c – 1 ~ … … |
l n ( 1 + ) ~ |
|
||||
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( 1 + ) p |
|
|
|
|
|
|
|
|
|
|
1 |
1 ~ ... |
|
|
– 1 ~ p |
|
|
В частности: |
1 1 ~ ... |
|
|||||||||
|
|
|
|
|
||||||||||
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Многоточиями здесь я хотел показать, что эти формулы не надо зазубривать, а надо уметь писать их на основе предыдущих формул.
|
|
|
|
2 . |
Т О Ч К И Р А З Р Ы В А . |
|
|
|
|
Функция y = f (x ) называется непрерывной в точке х 0 , если : |
|
|
|
||||||
1) (первое определение непрерывности) |
если предел функции в этой точке равен значению функции в этой точке, |
||||||||
т.е. |
. Рис. |
|
|
|
|
|
|
||
2) (второе определение непрерывности) |
если в этой точке бесконечно малому приращению функции соответст- |
||||||||
вует бесконечно малое приращение аргумента, т.е. |
. |
|
Рис |
|
|||||
Пусть функция |
f ( x ) определена в некоторой проколотой окрестности |
точки х 0 . При этом в са- |
|||||||
мой точке х 0 функция может быть определена, но может быть и не определена. |
Точка х 0 называется |
||||||||
т о ч к о й р а з р ы в а функции f ( x) , если не выполняется условие |
l i m |
f ( x ) f ( x0 ) . |
Это условие |
||||||
|
|
|
|
|
x x0 |
|
|
||
может не выполняться по следующим причинам: 1) функция f (x ) не определена в точке х 0 , |
2) предел |
||||||||
функции f ( x ) в точке |
х 0 не равен значению функции в этой точке , |
3) |
хотя бы один из односторонних |
||||||
пределов функции f ( x ) |
в точке |
х 0 не существует или бесконечен. |
|
|
|
|
|||
Точка разрыва |
х 0 называется т о ч к о й р а з р ы в а п е р в о г о р о д а , если в этой точке пределы |
||||||||
функции слева и справа существуют и конечны. |
|
|
|
|
|||||
Если хотя бы один из этих односторонних пределов не существует или бесконечен, то точка разры- |
|||||||||
ва называется т о ч к о й р а з р ы в а в т о р о г о р о д а . |
|
|
|
|
|||||
Признак точки разрыва. Если функция f ( x ) определена в некоторой проколотой окрестности точки |
|||||||||
х 0 , а в самой точке х 0 |
– не определена, |
то х 0 является точкой разрыва. |
(Этот признак формулирует достаточное условие точки разрыва) |
||||||
Рисунки … |
|
|
|
|
|
|
|
||
1) |
|
|
2) |
|
|
|
– пределы f ( x ) в точке раз- |
||
|
|
|
|
|
|||||
рыва слева и справа существуют и конечны.
3) 
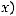

 4)
4) 
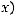


 – хотя бы один из односторонних пределов функции f ( x) в точке разрыва не существует или бесконечен.
– хотя бы один из односторонних пределов функции f ( x) в точке разрыва не существует или бесконечен.



- 3 -

Л е к т о р Л и с е е в И . А . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М И И Г А и К , |
|
Ф Э У Т 1 - 1 , 2 , 8 , |
о с е н ь 2 0 0 7 г . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 . Т Е Х Н И К А Д И Ф Ф Е Р Е Н Ц И Р О В А Н И Я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Определение производной для функции |
f ( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
в т о ч к е |
|
х : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f ( x ) |
|
|
|
|
|
|
|
|
|
||||||
f ' ( x ) l i m |
|
|
|
|
f ( x x ) f ( x ) |
f ( x + x ) |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
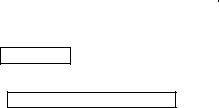
Г е о м е т р и ч е с к и й |
|
смысл производной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f ( x + x ) – f ( x ) |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
f ( x ) = k = t g . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Здесь y – это приращение функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
у = f(x) в точке х, |
соответствую- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x + x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
щее приращению аргумента x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а п р о и з в о д н ы х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н е к о т о р ы е п р а в и л а д и ф ф е - |
||||||||||||||||||||||||||||||||||||||||||
для "простых" функций |
для "сложных" функций |
|
|
|
|
|
р е н ц и р о в а н и я |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c – п о с т о я н н а я , |
c = 0 . |
||||||||||||||||||
А р г у м е н т x – н е з а в и - |
|
А р г у м е н т с а м я в л я е т с я |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
с и м а я п е р е м е н н а я . |
|
ф у н к ц и е й u = u ( x ) . |
|
|
|
u = u ( x ) , v = v ( x ) . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u 1 ( е с л и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u x ) |
|
|
|
С в о й с т в а л и н е й н о с т и . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
( x p ) = p x p – 1 |
|
( u p ) = p u p – 1 u |
|
|
|
[ u v ] = u v |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ с u ] = с u ; [ |
u |
]' |
1 |
u' |
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
( x )' x 2 |
|
|
( u )' u 2 u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
[ с + u ] = u , |
т . к . с = 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р о и з в о д н а я п р о и з в е д е н и я и |
|||||||||||||||||||||||
( |
|
x )' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( u )' |
|
|
|
|
|
|
u' |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч а с т н о г о ф у н к ц и й . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
|
|
|
|
|
|
|
2 |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( u v ) = u v + v u |
|
|
|
||||||||||||||||
( e x ) = e x |
|
|
( e u ) = e u u |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
u' v v' u |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
)' |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
( a x ) = a x l n a |
|
( a u ) = a u l n a u |
|
|
|
|
|
v |
|
|
|
|
v 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П р а в и л о д и ф ф е р е н ц и р о в а н и я |
||||||||||||||||||||
|
( ln x )' |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ln u )' |
|
|
|
|
1 |
u' |
|
|
|
|
|
|
|
|
|
с л о ж н о й ф у н к ц и и . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
Если у = у ( u ) , |
u = |
u ( x ) , то |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y'x y'u u'x . |
|
|
|
|
|
|
|
|
||||||||||||||
( log a x )' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( log a u )' |
|
|
|
|
u |
|
|
|
|
|
|
|
u' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
( s i n x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( s i n u ) |
= c o s u u |
|
Вычисление производной показатель- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
= c o s x |
|
|
но-степенной функции |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = ( x ) p ( x ) . |
|
|
|
|
|
|
|
|
||||||||
( c o s x ) |
|
= – s i n x |
|
( c o s u ) |
= – s i n u u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Первый способ (с использованием ос- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
новного логарифмического тождества): |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
( tg x )' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( tg u )' |
|
|
|
|
|
|
|
|
|
|
|
|
u' |
|
|
|
y = e |
l n … |
, |
|
y ' = … |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
cos 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 u |
|
|
|
|
|
|
|
|
|
Второй способ (с предварительным ло- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
( ctg u )' |
|
|
|
|
1 |
|
|
|
|
u' |
|
гарифмированием): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
( ctg x )' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l n y = |
l n ( x ) p ( x ) |
|
… |
|
|
|
|
|
|
… |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
sin 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
(arc sin x) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
(arc sin u) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
u' |
|
Вычисление производной функции, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заданной неявно. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( x , y ) = 0 ; |
|
|
|
|
y ' = ? |
||||||||||||||||||||||||||||||||||||||||||||||
(arc cos x) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(arc cos u) |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
u' |
|
|
Дифференцируем имеющееся соотноше- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние, помня, что |
у = у ( х ) |
! |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная функции, заданной пара- |
|||||||||||||||||||||
( arc tg x )' |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
( arc tg u )' |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
u' |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метрически … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
x 2 |
|
1 |
|
u 2 |
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x( t ) |
y x/ |
|
|
y |
t |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y ( t ) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t/ |
|
|
|
|||||||||||||||||||||
( arc ctg x )' |
|
|
|
|
|
|
|
|
|
|
( arc ctg u )' |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
u' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
1 x 2 |
|
1 |
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Д и ф ф е р е н ц и а л : |
если y = |
y ( x ) , |
|
то |
|
|
|
|
|
|
|
d y = y ' dx , |
|
|
|
|
где d x = |
x . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
При малых х |
|
имеет место приближѐнное равенство: |
|
|
d y y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
- 4 -
4 . П Р И Л О Ж Е Н И Я П Р О И З В О Д Н О Й |
|
|
|
|
||
|
|
|
|
|||
Форм ул а л ин еаризации : |
f ( x ) f ( x 0 ) + f ' ( x 0 ) ( x – x 0 ) |
|
(при х , близких к х 0 ) |
|||
Уравнение касательной y = f ( x 0 ) + f ' ( x 0 ) ( x – x 0 ) . Уравнение нормали … |
y f(x0 ) |
1 |
( x x0 ) |
|||
|
||||||
f'(x0 ) |
||||||
|
|
|
|
|
||
Алгебраический смысл дифференциала. Дифференциал приближѐнно равен приращению функции. d y = y ' x y .
Замечание. Приближѐнные равенства для функции (формула линеаризации) и для приращения функции ( у |
d y ) |
|
будут тем точнее, чем ближе наша функция к линейной функции в рассматриваемой точке х 0 и чем ближе х |
к х 0 |
|
(чем меньше х = х – х 0 ). |
Геометрический смысл дифференцируемости. |
|
Дифференцируемость функции означает существование касательной к графику этой функции.
|
0 |
|
|
|
l i m |
( x ) |
l i m |
' ( x ) |
|
Правил о Л опитал я (для раскрытия неопределѐнностей |
0 |
и |
|
): |
p( x ) |
p' ( x ) . |
|||
x |
x |
Форм ул а Т ейл ора (главная формула дифференциального исчисления):
|
|
|
|
f ( x ) |
f ( x ) |
f ' ( x0 ) |
( x |
x |
|
) ... ... |
|
|
f |
( n )( x0 ) |
( x |
x ) n |
R |
|
( x , x |
|
) |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
0 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
1! |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Формула Маклорена … |
|
|
|
|
f ( x ) f ( 0 ) |
|
f ' ( 0 ) |
|
|
x |
|
... ... |
|
f ( n )( 0 ) |
x n R |
|
( x ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1! |
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
МаклоренаФормулы функцийконкретныхдля |
|
|
|
|
|
|
e x 1 x |
x 2 |
|
|
|
|
x 3 |
|
... |
|
.. |
|
x n |
|
|
R , |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ! |
|
|
3 ! |
|
|
|
|
|
|
|
|
|
|
n ! |
|
|
|
|
|
n |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
l n ( 1 x ) x |
x 2 |
|
|
|
|
x 3 |
|
... |
.. ( 1 ) n 1 |
|
x n |
|
R |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
cos x |
1 |
|
x 2 |
|
|
|
|
x 4 |
|
... |
|
|
|
|
.. ( 1 ) n |
|
x 2n |
|
|
|
R |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2! |
|
|
|
4! |
|
|
|
|
|
|
( 2 n )! |
|
2n |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
s i n x x |
x 3 |
|
|
x 5 |
|
... |
|
|
|
|
.. ( 1 ) n |
|
x 2n 1 |
|
|
|
R |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 ! |
|
5 ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2 n |
1 )! |
|
|
|
|
2n 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
И С С Л Е Д О В А Н И Е Ф У Н К Ц И Й … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
Признак точки разрыва. Если в некоторой проколотой окрестности точки х = с функция f ( x ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определена, а в самой точке х = с не определена, то |
|
х |
= с – |
точка разрыва функции |
f ( x ) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
А с и м п т о т ы . |
Вертикальные асимптоты могут быть "в точках" разрыва и на границе области опре- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
деления функции. Невертикальные асимптоты для графика функции у = f ( x ) |
описываются уравнением |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
у = k x + |
b , |
|
где |
k |
|
|
|
l i m |
|
|
f ( x ) |
|
|
|
и |
b |
|
l i m |
[ f ( x ) k x ] . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Невертикальные асимптоты могут быть правыми (при х |
|
→ + ∞ ) |
и левыми (при х |
→ – ∞ ). Если k |
или b равно |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
∞ или не существует, |
то не существует и асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
П е р в а я п р о и з в о д н а я : |
возрастание, убывание, точки экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
f ( x ) |
> |
0 |
f ( x ) возрастает; |
|
|
|
|
f ( x ) |
< |
0 |
|
|
|
|
|
f ( x ) убывает. |
||||||||||||||||||||||||||||||||||||||
|
В т о р а я п р о и з в о д н а я : |
выпуклость, вогнутость, точки перегиба. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
f ( x ) < 0 |
|
|
график выпуклый; |
|
|
|
|
|
|
f ( x ) > |
0 |
|
|
график вогнутый |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
П л а н и с с л е д о в а н и я ф у н к ц и й … |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
1. |
Найти |
.о б л а с т ь о п р е д е л е н и я |
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2. |
Выявить (если они есть) |
|
.з а к о н о м е р н о с т и |
|
функции (и графика): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
1) функция четная (график симметричен относительно оси O у ) |
или |
функция нечетная (график симметри- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
чен относительно начала координат), |
или функция общего вида (нет симметрий, как в предыдущих случаях), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2)функция периодическая или непериодическая.
3.Вычисляя .п р е д е л ы , исследовать точки разрыва, найти асимптоты. И уже следует начать (пока схематично)
строить график. Можно ещѐ посмотреть, как ведѐт себя функция на границе области определения и на бесконечности (при х
)
4. Вычислить .п е р в у ю п р о и з в о д н у ю . Найти критические точки функции (где первая производная равна
нулю или терпит разрыв). Указать интервалы возрастания и убывания функции. Указать точки максимума и минимума.
5. |
Вычислить |
.в т о р у ю п р о и з в о д н у ю |
. Найти точки, где вторая производная равна нулю или терпит раз- |
||||
рыв. |
Указать участки выпуклости и вогнутости графика. |
Указать точки перегиба. |
|||||
6. |
Вычислить координаты |
.х а р а к т е р н ы х т о ч е к г р а ф и к а |
(пересечения с осями координат, а также точ- |
||||
ки, где первая и вторая производная равны нулю или терпят разрыв). |
|||||||
7. |
Аккуратно и, по возможности, точно нарисовать |
.г р а ф и к |
функции, отметив на нѐм характерные точки. |
||||
Чтобы получить более точный график можно "посчитать" и нанести на график ещѐ несколько точек.
- 5 -

Л е к т о р Л и с е е в И . А . |
|
|
|
М И И Г А и К , Ф Э У Т 1 - 1 , 2 , 8 , о с е н ь 2 0 0 7 г . |
|
5 . |
П Е Р В О О Б Р А З Н Ы Е |
||||
|
|||||
|
|
||||
|
|
|
|
||
П е р в о о б р а з н о й д л я ф у н к ц и и |
f ( x ) называется такая функция F ( x ) , производная |
||||
от которой равна функции f ( x ) : F ( x ) = f ( x ) . Если у функции f ( x ) есть хоть одна первообраз- |
|||||
ная, то у неѐ есть бесчисленное множество первообразных. |
|||||
Если F ( x ) – одна из первообразных для функции f ( x ) , то всѐ множество еѐ первообраз- |
|||||
ных описывается выражением: |
F ( x ) + С , |
где С – произвольная постоянная. |
|||
Всѐ множество первообразных F ( x ) + С для функции f ( x ) называется н е о п р е д е л ѐ н - н ы м и н т е г р а л о м для этой функции и обозначается f ( x ) dx . Таким образом,
f ( x ) dx F( x ) C .
При вычислении неопределѐнных интегралов (первообразных) постоянный множитель можно вынести за знак интеграла, интеграл от суммы (разности) функций равен сумме (разности) интегралов.
Иногда символом f ( x ) dx обозначают только какую-либо одну первообразную для функции f ( x ) .
И мы в таблице первообразных указываем только одну первообразную, а не всѐ их множество.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а п е р в о о б р а з н ы х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подведения под знак дифференциала |
|||||||||||||||||||||||
Для "простых" функций (аргумент |
|
Для "сложных" функций (аргумент |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
– независимая переменная). |
|
|
|
|
сам является функцией) |
|
u = u ( x ) . |
|
|
|
|
|
|
|
|
|
|
|
|
d x = |
|
d ( x c ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d u u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x = – d ( – x ) |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
p |
dx |
|
x p 1 |
|
|
|
|
|
|
|
|
|
u |
p |
|
du |
|
|
|
|
u p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
1 |
d ( k x ) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x k d ( |
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |x| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |u| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
e x dx e x |
|
|
|
|
|
|
|
|
|
|
|
e u du e u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x d x |
d x 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|
|
|
|
|
|
a u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a x dx |
|
|
|
|
|
|
|
|
|
|
a u du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x d x = d e x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
d ln x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
cos x dx |
sin x |
|
|
|
|
|
|
|
|
cos u du |
sin u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c o s x d x = d s i n x |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
sin x dx |
|
|
|
cos x |
|
|
|
|
|
|
|
sin u du |
cos u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s i n x d x |
|
|
|
= – d c o s x |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
tg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
tg u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d tg x |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos |
2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
ctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
ctg u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
d ctg x |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
sin 2 x |
|
|
|
|
|
|
|
|
sin 2 u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 x |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
arc sin x |
|
|
|
|
|
|
|
|
|
|
|
d u |
|
|
|
|
|
|
|
arc sin u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
|
|
d arc sin x |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
|
|
|
1 u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
arctg x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
arctg u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
d arc tg x |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
x 2 1 |
|
|
|
|
|
|
|
|
|
|
u 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
|
|
arc sin |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d u |
|
|
|
|
arc sin |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
a 2 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 2 u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулы интегрирования |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
u |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совершенно одинаковые, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x 2 |
a 2 |
|
|
a arc tg a |
|
|
|
|
|
|
|
|
|
|
|
|
|
u 2 |
a 2 |
|
|
a arc tg a |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что для простых функций, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что для сложных. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
u a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l n | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l n | |
|
|
Этот факт называется свойством |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
x 2 a |
2 |
|
|
|
|
|
2 a |
x a |
|
|
|
|
|
|
|
|
u 2 a |
2 |
|
|
2 a |
u a |
|
|
|
|
инвариантности формул интег- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рирования. |
||||||||
|
|
|
|
d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
l n | x |
x 2 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l n | u |
|
u 2 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
x 2 |
|
|
|
|
|
|
|
u 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
- 6 -

6 . Н Е К О Т О Р Ы Е П Р А В И Л А И Ф О Р М У Л Ы И Н Т Е Г Р И Р О В А Н И Я
Свойства линейности для первообразных (для неопределѐнного интеграла) и для определѐнного интеграла.
Интеграл от суммы или разности функций равен сумме или разности интегралов от этих функций. Постоянный множитель можно вынести за знак интеграла. И постоянный множитель можно вне-
сти под знак интеграла. (Во всяком случае, если этот постоянный множитель отличен от нуля)
Свойство аддитивности интеграла по области интегрирования ……
З а м е н а п е р е м е н н о й |
2. Надо получить соотношение |
4. |
От исходного интеграла надо перейти |
||||||||||
между дифференциалами: |
к интегралу с новой переменной. |
||||||||||||
п р и и н т е г р и р о в а н и и . |
|||||||||||||
d x = … . d t |
или d t |
= … d x . |
5. |
Теперь надо вычислить интеграл с |
|||||||||
1. Надо иметь соотношение |
|||||||||||||
3 . Если мы вычисляем опреде- |
новой переменной. |
|
|
||||||||||
между старой и новой пере- |
|
|
|||||||||||
лѐнный интеграл, то надо пере- |
6. Если мы вычисляем неопределѐнный |
||||||||||||
менными: |
|
||||||||||||
|
считать пределы изменения пе- |
интеграл, то надо вернуться к старой |
|||||||||||
x = x ( t ) |
или t = t ( x ) . |
||||||||||||
ременной. |
|
|
|
переменной. |
|
|
|||||||
|
|
|
|
|
|
|
|||||||
. Ф о р м у л а и н т е г р и р о в а н и я |
u |
dv u v v du |
|
b |
|
b |
b |
||||||
|
|
||||||||||||
|
|
u dv u v |
v du |
||||||||||
|
|
||||||||||||
|
п о ч а с т я м : |
|
|
a |
|||||||||
|
|
|
|
|
|
|
|
a |
|
a |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
b |
|
|
l i m |
n |
|
|
|||
О п р е д е л е н и е о п р е д е л ѐ н н о г о |
|
f ( x ) d x |
f ( xi ) xi |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
и н т е г р а л а |
|
|
a |
|
n |
|
i 1 |
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
все хi |
0 |
|
|
|||
|
Ф о р м ул а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
|
|
|
||
Ньютона – Лейбница |
|
|
f ( x ) dx |
F( x ) |
F( b ) F( a ) |
|
|||||||
|
|
|
|
||||||||||
( г л а в н а я ф о р м у л а |
|
|
|
a |
|
||||||||
|
|
|
a |
|
|
|
|
|
|
||||
и н т е г р а л ь н о г о и с ч и с л е н и я ) : |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
b |
|
|
n |
|
|
|
|
|
|
|
Ф о р м у л а п р я м о у г о л ь н и к о в |
f ( x ) d x f ( xi ) xi |
|
|
Рисунок |
|||||||||
|
|
|
a |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Н е с о б с т в е н н ы е и н т е г р а л ы |
|
опр |
|
|
|
|
|
|
|||||
|
f ( x ) dx … … … |
|
|
|
|
||||||||
п о б е с к о н е ч н о м у п р о м е - |
|
|
|
|
|
||||||||
ж у т к у и н т е г р и р о в а н и я |
|
a |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Н е с о б с т в е н н ы е и н т е г р а л ы |
|
b |
опр |
|
|
|
|
|
|
||||
о т н е о г р а н и ч е н н ы х ф у н к ц и й |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
f ( x ) dx … … … |
|
|
|
|
||||||||
( l i m f ( x ) ) |
|
|
|
|
|
|
|||||||
x a |
|
|
a |
|
|
|
|
|
|
|
|||
|
|||||||||||||
Замечание. При вычислении несобственных интегралов иногда используют следующие |
|||||||||||||
краткие обозначения. Если f ( ) |
не определено, |
то под записью |
f ( ) понимают |
l i m f ( x ) , |
|||||||||
где и |
f ( ) могут быть конечными или бесконечными определѐнного знака. |
|
x |
||||||||||
При такой договорѐнности для несобственных интегралов тоже можно писать формулу Ньютона-Лейбница.
==== При вычислении интегралов часто приходится разбивать подынтегральную функцию на сумму двух (или нескольких) слагаемых. В простейшем случае почленного деления числителя на знаменатель "рабо-
тает" школьная формула |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При вычислении интеграла от рациональной дроби |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
надо прежде всего выделить в этой дроби целую часть |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(если эта дробь – неправильная). |
Здесь мы тоже подын- |
неправ. рац. дробь |
целая часть прав. рац. дробь |
|||||||||||||||||
тегральную функцию разбиваем на сумму . |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7 . П Р И Л О Ж Е Н И Я И Н Т Е Г Р А Л А
Вычисление площадей …
Вычисление длин дуг кривых ….
- 7 -
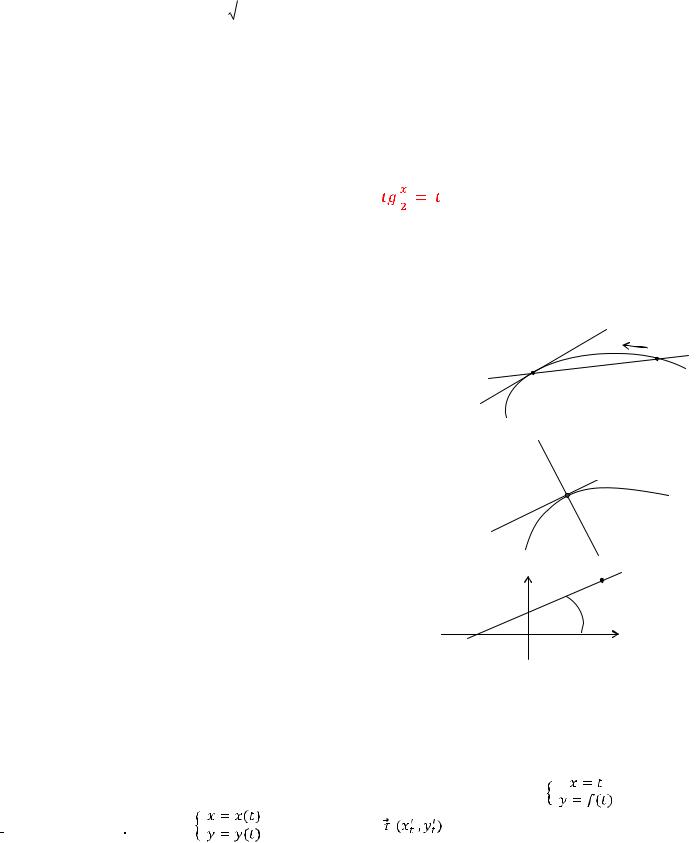
Вычисление объѐма тела по известным площадям его параллельных сечений …
8 . " Н Е Б Е Р У Щ И Е С Я " И Н Т Е Г Р А Л Ы
e x 2 d x ; |
|
cos x |
d x ; |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||
|
x cos x d x ; |
|
|
d x |
… |
|
|
|
|||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
ln x |
|
|
|
|
||||||
|
|
|
|
9 . Н Е К О Т О Р Ы Е Ф О Р М У Л Ы Т Р И Г О Н О М Е Т Р И И . |
|
|
|||||||||||||||
Основное тригонометрическое тождество … |
|
|
|
Формулы двойного аргумента. |
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
Формулы понижения степени … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Преобразование произведений в сумму … |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для универсальной тригонометрической подстановки |
|
|
|
|
|
|
|
нужны формулы, выражающие |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
co s x, |
s in x , t g x |
через тангенс половинного аргумента. |
Я, правда, такие примеры двоечникам, да и троеч- |
|
|||||||||||||||||
никам, не даю. |
Более простых примеров им вполне хватает. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 0 . |
К А С А Т Е Л Ь Н А Я И Н О Р М А Л Ь |
|
|
|||||||||||||
График функции может быть гладкой (плавной) кривой, а может иметь "изломы". Там, где график – гладкая кривая, |
|
||||||||||||||||||||
там в каждой точке графика можно провести касательную. |
А в точке излома касательную провести нельзя. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к а с а т е л ьн а я |
|
Определение касательной к кривой. |
Рассмотрим точки М и S |
M |
S |
|
|||||||||||||||||
на кривой |
L и секущую М S . |
Пусть точка М фиксирована, |
|
|
|||||||||||||||||
а точка |
S |
(по кривой p ) неограниченно приближается к точке М . |
с е к у щ а я |
p |
|||||||||||||||||
|
|
||||||||||||||||||||
К а с а т е л ь н о й к к р и в о й |
p |
в т о ч к е |
М |
|
|
называется |
|
|
|||||||||||||
предельное положение секущей М S |
при стремлении точки S |
|
|
|
|
||||||||||||||||
по кривой L |
к точке М . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Н о р м а л ь ю к к р и в о й в т о ч к е М называется прямая, перпендикулярная касательной к этой кривой в точке М .
П р я м а я н а п л о с к о с т и . |
|
Уравнение прямой с угловым коэффициентом : |
y = k x + b . |
( k = t g – угловой коэффициент прямой) |
|
н орм ал ь к а с а т е л ьн а я
к р и в а я
М
М ( x 0 , у 0 )
Уравнение прямой, проходящей через точку ( х 0 , у 0 ) , с угловым коэффициентом k : |
y = |
y 0 + k ( x – x 0 ) . |
|||||||||||||||||||||||||||||||||||
Уравнения касательной и нормали к графику функции |
y |
= f ( x ) в точке ( х 0 , |
у 0 ) , |
где у 0 = f (x 0 ) . |
|
||||||||||||||||||||||||||||||||
Ур. касательной: y = f (x 0 ) + f ' (x 0 ) (x – x 0 ). |
Ур. нормали: |
y f ( x0 ) |
|
1 |
|
( x x0 |
) |
||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
f ' ( x0 ) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
== = От обычного задания функции |
y = f (x ) легко перейти к параметрическому: |
|
|
|
|
. |
|
||||||||||||||||||||||||||||||
Вектор касательной к кривой |
находится так : |
. |
Вектор нормали можно найти из |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
условия перпендикулярности . … |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 8 - |
|
|
T h e |
E n d |
|
|
||||
