
- •Contents
- •Preface to the second edition
- •Preface to the first edition
- •1 Special relativity
- •1.2 Definition of an inertial observer in SR
- •1.4 Spacetime diagrams
- •1.6 Invariance of the interval
- •1.8 Particularly important results
- •Time dilation
- •Lorentz contraction
- •Conventions
- •Failure of relativity?
- •1.9 The Lorentz transformation
- •1.11 Paradoxes and physical intuition
- •The problem
- •Brief solution
- •2 Vector analysis in special relativity
- •Transformation of basis vectors
- •Inverse transformations
- •2.3 The four-velocity
- •2.4 The four-momentum
- •Conservation of four-momentum
- •Scalar product of two vectors
- •Four-velocity and acceleration as derivatives
- •Energy and momentum
- •2.7 Photons
- •No four-velocity
- •Four-momentum
- •Zero rest-mass particles
- •3 Tensor analysis in special relativity
- •Components of a tensor
- •General properties
- •Notation for derivatives
- •Components
- •Symmetries
- •Circular reasoning?
- •Mixed components of metric
- •Metric and nonmetric vector algebras
- •3.10 Exercises
- •4 Perfect fluids in special relativity
- •The number density n
- •The flux across a surface
- •Number density as a timelike flux
- •The flux across the surface
- •4.4 Dust again: the stress–energy tensor
- •Energy density
- •4.5 General fluids
- •Definition of macroscopic quantities
- •First law of thermodynamics
- •The general stress–energy tensor
- •The spatial components of T, T ij
- •Conservation of energy–momentum
- •Conservation of particles
- •No heat conduction
- •No viscosity
- •Form of T
- •The conservation laws
- •4.8 Gauss’ law
- •4.10 Exercises
- •5 Preface to curvature
- •The gravitational redshift experiment
- •Nonexistence of a Lorentz frame at rest on Earth
- •The principle of equivalence
- •The redshift experiment again
- •Local inertial frames
- •Tidal forces
- •The role of curvature
- •Metric tensor
- •5.3 Tensor calculus in polar coordinates
- •Derivatives of basis vectors
- •Derivatives of general vectors
- •The covariant derivative
- •Divergence and Laplacian
- •5.4 Christoffel symbols and the metric
- •Calculating the Christoffel symbols from the metric
- •5.5 Noncoordinate bases
- •Polar coordinate basis
- •Polar unit basis
- •General remarks on noncoordinate bases
- •Noncoordinate bases in this book
- •5.8 Exercises
- •6 Curved manifolds
- •Differential structure
- •Proof of the local-flatness theorem
- •Geodesics
- •6.5 The curvature tensor
- •Geodesic deviation
- •The Ricci tensor
- •The Einstein tensor
- •6.7 Curvature in perspective
- •7 Physics in a curved spacetime
- •7.2 Physics in slightly curved spacetimes
- •7.3 Curved intuition
- •7.6 Exercises
- •8 The Einstein field equations
- •Geometrized units
- •8.2 Einstein’s equations
- •8.3 Einstein’s equations for weak gravitational fields
- •Nearly Lorentz coordinate systems
- •Gauge transformations
- •Riemann tensor
- •Weak-field Einstein equations
- •Newtonian limit
- •The far field of stationary relativistic sources
- •Definition of the mass of a relativistic body
- •8.5 Further reading
- •9 Gravitational radiation
- •The effect of waves on free particles
- •Measuring the stretching of space
- •Polarization of gravitational waves
- •An exact plane wave
- •9.2 The detection of gravitational waves
- •General considerations
- •Measuring distances with light
- •Beam detectors
- •Interferometer observations
- •9.3 The generation of gravitational waves
- •Simple estimates
- •Slow motion wave generation
- •Exact solution of the wave equation
- •Preview
- •Energy lost by a radiating system
- •Overview
- •Binary systems
- •Spinning neutron stars
- •9.6 Further reading
- •10 Spherical solutions for stars
- •The metric
- •Physical interpretation of metric terms
- •The Einstein tensor
- •Equation of state
- •Equations of motion
- •Einstein equations
- •Schwarzschild metric
- •Generality of the metric
- •10.5 The interior structure of the star
- •The structure of Newtonian stars
- •Buchdahl’s interior solution
- •10.7 Realistic stars and gravitational collapse
- •Buchdahl’s theorem
- •Quantum mechanical pressure
- •White dwarfs
- •Neutron stars
- •10.9 Exercises
- •11 Schwarzschild geometry and black holes
- •Black holes in Newtonian gravity
- •Conserved quantities
- •Perihelion shift
- •Post-Newtonian gravity
- •Gravitational deflection of light
- •Gravitational lensing
- •Coordinate singularities
- •Inside r = 2M
- •Coordinate systems
- •Kruskal–Szekeres coordinates
- •Formation of black holes in general
- •General properties of black holes
- •Kerr black hole
- •Dragging of inertial frames
- •Ergoregion
- •The Kerr horizon
- •Equatorial photon motion in the Kerr metric
- •The Penrose process
- •Supermassive black holes
- •Dynamical black holes
- •11.6 Further reading
- •12 Cosmology
- •The universe in the large
- •The cosmological arena
- •12.2 Cosmological kinematics: observing the expanding universe
- •Homogeneity and isotropy of the universe
- •Models of the universe: the cosmological principle
- •Cosmological metrics
- •Cosmological redshift as a distance measure
- •The universe is accelerating!
- •12.3 Cosmological dynamics: understanding the expanding universe
- •Critical density and the parameters of our universe
- •12.4 Physical cosmology: the evolution of the universe we observe
- •Dark matter and galaxy formation: the universe after decoupling
- •The early universe: fundamental physics meets cosmology
- •12.5 Further reading
- •Appendix A Summary of linear algebra
- •Vector space
- •References
- •Index

220 |
Gravitational radiation |
Measuring distances with light
One of the most convenient ways of measuring the range to a distant object is by radar: send out a pulse of electromagnetic radiation, measure how long it takes to return after reflecting from the distant object, divide that by two and multiply by c, and that is the distance. Remarkably, because light occupies such a privileged position in the theory of relativity, this method is also an excellent way of measuring proper distances even in curved spacetime. It is the foundation of laser interferometric gravitational wave detectors.
We shall compute how to use light to measure the distance between two freely falling objects. Because the objects are freely falling, and because we make no assumption that they are close to one another, we shall use the TT coordinate system. Let us consider for simplicity at first a wave traveling in the z-direction with pure +–polarization, so that the metric is given by
ds2 = −dt2 + [1 + h+(z − t)]dx2 + [1 − h+(t − z)]dy2 + dz2. |
(9.58) |
Suppose, again for simplicity, that the two objects lie on the x-axis, one of them at the origin x = 0 and the other at coordinate location x = L. In TT coordinates, they remain at these coordinate locations all the time. To make our measurement, the object at the origin sends a photon along the x-axis toward the other object, which reflects it back. The first object measures the amount of proper time that has elapsed since first emitting the photon. How is this related to the distance between the objects and to the metric of the gravitational wave?
Note that a photon traveling along the x-axis moves along a null world line (ds2 = 0) with dy = dz = 0. That means that it has an effective speed
dt |
|
2 |
= |
1 + h+ . |
(9.59) |
||
|
dx |
|
|
1 |
|
|
|
Although this is not equal to one, this is just a coordinate speed, so it does not contradict relativity. A photon emitted at time tstart from the origin reaches any coordinate location x in a time t(x); this is essentially what we are trying to solve for. The photon reaches the other end, at the fixed coordinate position x = L, at the coordinate time given by integrating the effective speed of light from Eq. (9.59):
tfar = tstart + ' L "1 + h+(t(x))#1/2 dx. (9.60)
0
This is an implicit equation since the function we want to find, t(x), is inside the integral. But in linearized theory, we can solve this by using the fact that h+ is small. Where t(x) appears in the argument of h+, we can use its flat-spacetime value, since corrections due to h+ will only bring in terms of order h2+ in Eq. (9.60). So we set t(x) = tstart + x inside the integral and expand the square root. The result is the explicit integration
tfar = tstart + L + 21 |
' |
h+(tstart + x)dx. |
|
|
L |
0

221 |
9.2 The detection of gravitational waves |
The light is reflected back, and a similar argument gives the total time for the return trip:
treturn = tstart + 2L + 21 |
'0 |
h+(tstart + x)dx + 21 |
'0 |
h+(tstart + L + x)dx. |
(9.61) |
|
L |
|
|
L |
|
Note that coordinate time t in the TT coordinates is proper time, so that this equation gives a value that can be measured.
What does this equation tell us? First, suppose that L is actually rather small compared to the gravitational wavelength, or equivalently that the return time is small compared to the period of the wave, so that h+ is effectively constant during the flight of the photon. Then the return time is just proportional to the proper distance to L as measured by this metric. This should not be surprising: for a small separation we could set up a local inertial frame in free fall with the particles, and in this frame all experiments should come out as they do in special relativity. In SR we know that radar ranging gives the correct proper distance, so it must do so here as well.
More generally, how do we use this equation to measure the metric of the wave? The simplest way to use it is to differentiate treturn with respect to tstart, i.e. to monitor the rate of change of the return time as the wave passes. Since the only way that tstart enters the integrals in Eq. (9.61) is as the argument tstart + x of h+, a derivative of the integral operates only as a derivative of h+ with respect to its argument. Then the integration with respect to x is an integral of the derivative of h+ over its argument, which simply produces h+ again. The result of this is the vastly simpler expression
dtstart |
= 1 + 21 "h+(tstart + 2L) − h+(tstart)# . |
(9.62) |
dtreturn |
|
|
This is rather a remarkable result: the rate of change of the return time depends only on the metric of the wave at the time the wave was emitted and when it was received back at the origin. In particular, the wave amplitude when the photon reflected off the distant object plays no role.
Now, if the signal sent out from the origin is not a single photon but a continuous electromagnetic wave with some frequency ν, then each ‘crest’ of the wave can be thought of as another null ray or another photon being sent out and reflected back. The derivative of the time it takes these rays to return is nothing more than the change in the frequency of the electromagnetic wave:
dtreturn = νreturn . dtstart νstart
So if we monitor changes in the redshift of the returning wave, we can relate that directly to changes in the amplitude of the gravitational waves.
So far we have used a rather special arrangement of objects and wave: the wave was traveling in a direction perpendicular to the separation of the objects. If instead the wave is traveling at an angle θ to the z axis in the x − −z plane, the return time derivative does involve the wave amplitude at the reflection time:
dtreturn |
= 1 + 21 {(1 − sin θ )h+(tstart + 2L) − (1 |
+ sin θ )h+(tstart) |
dtstart |
||
|
+2 sin θ h+[tstart + (1 − sin θ )L]} . |
(9.63) |

222 |
Gravitational radiation |
This three-term relation is the starting point for analyzing the response of beam detectors, as we shall see next. For its derivation see, Exer. 27, § 9.7.
Beam detectors
The simplest beam detector is spacecraft tracking (Armstrong 2006). Interplanetary spacecraft carry transponders, which are radio receivers that amplify and return the signals they receive from the ground tracking station. A measurement of the return time of the signal tells the space agency how far away the spacecraft is. If the measurement is accurate enough, small changes in the return time might be caused by gravitational waves. In practice, this is a difficult measurement to make, because fluctuations might also be caused by changes in the index of refraction of the thin interplanetary plasma or of the ionosphere, both of which the signals must pass through. These effects can be discriminated from a true gravitational wave by using the three-term relation, Eq. (9.63). The detected waveform has to appear in three different places in the data, once with the opposite sign. Random fluctuations are unlikely to do this.
Plasma fluctuations can also be suppressed by using multiple transponding frequencies (allowing them to be measured) or by using higher-frequency transponding, even using infrared laser light, which is hardly affected by plasma at all. But even then there will be another limit on the accuracy: the stability of the clock at the tracing station that measures the elapsed time treturn. Even the best clocks are, at present, not stable at the 10−19 level. It follows that a beam detector of this type could not expect to measure gravitational waves with amplitudes of 10−20 or below. Unfortunately, as we shall see below, this is where we expect almost all amplitudes to lie.
The remedy is to use an interferometer. In an interferometer, light from a stable laser passes through a beam splitter, which sends half the light down one arm and the other half down a perpendicular arm. The two beams of light have correlated phases. When they return after reflecting off mirrors at the ends of the arms, they are brought back into interference (see Fig. 9.3). The interference measures the difference in the arm-lengths of the two arms. If this difference changes, say because a gravitational wave passes through, then the interference pattern changes and the wave can in principle be detected.
Now, an interferometer can usefully be thought of as two beam detectors laid perpendicular to one another. The two beams are correlated in phase: any given ‘crest’ of the light wave starts out down both arms at the same time. If the arms have the same proper length, then their beams will return in phase, interfering constructively. If the arms differ, say, by half the wavelength of light, then they will return out of phase and they will destructively interfere. An interferometer solves the problem that a beam detector needs a stable clock. The ‘clock’ in this case is one of the arms. The time-travel of the light in one arm essentially provides a reference for the return time of the light in the other arm. The technology of lasers, mirrors, and other systems is such that this reference can be used to measure changes in the return travel time of the other arm much more stably than the best atomic clocks would be able to do.
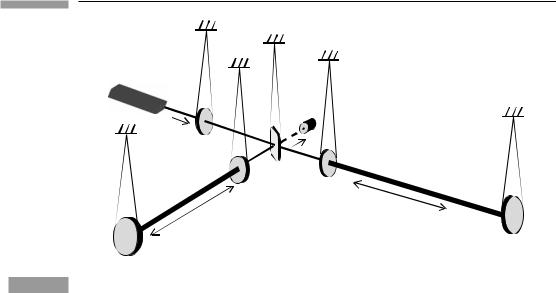
223 |
9.2 The detection of gravitational waves |
Figure 9.3
Laser
Photodetector
Power recycling mirror
Beam splitter |
Arm 2 |
Arm 1 |
Near |
|
mirror |
Far mirror
Sketch of the configuration of an interferometer like LIGO or VIRGO. Light from the laser passes through the power recycling mirror to the beamsplitter, where it is divided between the two arms. The arms form cavities, trapping most of the light, because the near mirrors are almost fully reflecting. This power buildup increases the sensitivity. The light exiting the cavities returns to the beamsplitter. A beam with destructive interference (difference of amplitudes) goes toward the photodetector; it should be dark unless a gravitational wave is present. The other return beam from the beamsplitter is the constructive interference beam returning toward the laser. Almost all the light goes here, and in order not to waste it, the power recycling mirror returns it to the interferometer in phase with the new incoming laser light. All the mirrors, including the beamsplitter, are suspended in order to filter out mechanical vibration noise. Other refinements of the optical design, such as mode cleaners and signal recycling mirrors, are not illustrated. The diagram is not to scale: the arms are 3 to 4 km long, while the central area (near mirrors, beamsplitter, laser, photodetector) is contained in a single building.
Interferometers are well-suited to registering gravitational waves: to see how this works, look at the polarization diagram Fig. (9.1). Imagine putting an interferometer in the circle in panel (a), with the beamsplitter at the center and the ends of the arms where the circle intersects the x- and y-directions. Then when a wave with +–polarization arrives, as in panel (b), it will stretch one arm and at the same time compress the other. This doubles the effective armlength difference that the interference pattern measures. But even if the wave arrives from, say, the x-direction, then its transverse action will still compress and expand the y-arm, giving a signal half as large as the maximum. But a wave of ×-polarization, as in panel (c), arriving perpendicular to both arms, will not stretch the interferometer arms at all, and so will not be detected. The interferometer is therefore a linearly polarized detector that responds to signals arriving from almost all directions.
Because interferometers bring light beams together and interfere them, it is often mistakenly thought that they measure the changes in their armlengths against a standard wavelength, and that in turn sometimes leads students to ask whether the wavelength of light is affected by the gravitational wave, thereby invalidating the measurement. Our discussion of beam detectors should make clear that the wavelength of the light is not the
