
- •Contents
- •Preface to the second edition
- •Preface to the first edition
- •1 Special relativity
- •1.2 Definition of an inertial observer in SR
- •1.4 Spacetime diagrams
- •1.6 Invariance of the interval
- •1.8 Particularly important results
- •Time dilation
- •Lorentz contraction
- •Conventions
- •Failure of relativity?
- •1.9 The Lorentz transformation
- •1.11 Paradoxes and physical intuition
- •The problem
- •Brief solution
- •2 Vector analysis in special relativity
- •Transformation of basis vectors
- •Inverse transformations
- •2.3 The four-velocity
- •2.4 The four-momentum
- •Conservation of four-momentum
- •Scalar product of two vectors
- •Four-velocity and acceleration as derivatives
- •Energy and momentum
- •2.7 Photons
- •No four-velocity
- •Four-momentum
- •Zero rest-mass particles
- •3 Tensor analysis in special relativity
- •Components of a tensor
- •General properties
- •Notation for derivatives
- •Components
- •Symmetries
- •Circular reasoning?
- •Mixed components of metric
- •Metric and nonmetric vector algebras
- •3.10 Exercises
- •4 Perfect fluids in special relativity
- •The number density n
- •The flux across a surface
- •Number density as a timelike flux
- •The flux across the surface
- •4.4 Dust again: the stress–energy tensor
- •Energy density
- •4.5 General fluids
- •Definition of macroscopic quantities
- •First law of thermodynamics
- •The general stress–energy tensor
- •The spatial components of T, T ij
- •Conservation of energy–momentum
- •Conservation of particles
- •No heat conduction
- •No viscosity
- •Form of T
- •The conservation laws
- •4.8 Gauss’ law
- •4.10 Exercises
- •5 Preface to curvature
- •The gravitational redshift experiment
- •Nonexistence of a Lorentz frame at rest on Earth
- •The principle of equivalence
- •The redshift experiment again
- •Local inertial frames
- •Tidal forces
- •The role of curvature
- •Metric tensor
- •5.3 Tensor calculus in polar coordinates
- •Derivatives of basis vectors
- •Derivatives of general vectors
- •The covariant derivative
- •Divergence and Laplacian
- •5.4 Christoffel symbols and the metric
- •Calculating the Christoffel symbols from the metric
- •5.5 Noncoordinate bases
- •Polar coordinate basis
- •Polar unit basis
- •General remarks on noncoordinate bases
- •Noncoordinate bases in this book
- •5.8 Exercises
- •6 Curved manifolds
- •Differential structure
- •Proof of the local-flatness theorem
- •Geodesics
- •6.5 The curvature tensor
- •Geodesic deviation
- •The Ricci tensor
- •The Einstein tensor
- •6.7 Curvature in perspective
- •7 Physics in a curved spacetime
- •7.2 Physics in slightly curved spacetimes
- •7.3 Curved intuition
- •7.6 Exercises
- •8 The Einstein field equations
- •Geometrized units
- •8.2 Einstein’s equations
- •8.3 Einstein’s equations for weak gravitational fields
- •Nearly Lorentz coordinate systems
- •Gauge transformations
- •Riemann tensor
- •Weak-field Einstein equations
- •Newtonian limit
- •The far field of stationary relativistic sources
- •Definition of the mass of a relativistic body
- •8.5 Further reading
- •9 Gravitational radiation
- •The effect of waves on free particles
- •Measuring the stretching of space
- •Polarization of gravitational waves
- •An exact plane wave
- •9.2 The detection of gravitational waves
- •General considerations
- •Measuring distances with light
- •Beam detectors
- •Interferometer observations
- •9.3 The generation of gravitational waves
- •Simple estimates
- •Slow motion wave generation
- •Exact solution of the wave equation
- •Preview
- •Energy lost by a radiating system
- •Overview
- •Binary systems
- •Spinning neutron stars
- •9.6 Further reading
- •10 Spherical solutions for stars
- •The metric
- •Physical interpretation of metric terms
- •The Einstein tensor
- •Equation of state
- •Equations of motion
- •Einstein equations
- •Schwarzschild metric
- •Generality of the metric
- •10.5 The interior structure of the star
- •The structure of Newtonian stars
- •Buchdahl’s interior solution
- •10.7 Realistic stars and gravitational collapse
- •Buchdahl’s theorem
- •Quantum mechanical pressure
- •White dwarfs
- •Neutron stars
- •10.9 Exercises
- •11 Schwarzschild geometry and black holes
- •Black holes in Newtonian gravity
- •Conserved quantities
- •Perihelion shift
- •Post-Newtonian gravity
- •Gravitational deflection of light
- •Gravitational lensing
- •Coordinate singularities
- •Inside r = 2M
- •Coordinate systems
- •Kruskal–Szekeres coordinates
- •Formation of black holes in general
- •General properties of black holes
- •Kerr black hole
- •Dragging of inertial frames
- •Ergoregion
- •The Kerr horizon
- •Equatorial photon motion in the Kerr metric
- •The Penrose process
- •Supermassive black holes
- •Dynamical black holes
- •11.6 Further reading
- •12 Cosmology
- •The universe in the large
- •The cosmological arena
- •12.2 Cosmological kinematics: observing the expanding universe
- •Homogeneity and isotropy of the universe
- •Models of the universe: the cosmological principle
- •Cosmological metrics
- •Cosmological redshift as a distance measure
- •The universe is accelerating!
- •12.3 Cosmological dynamics: understanding the expanding universe
- •Critical density and the parameters of our universe
- •12.4 Physical cosmology: the evolution of the universe we observe
- •Dark matter and galaxy formation: the universe after decoupling
- •The early universe: fundamental physics meets cosmology
- •12.5 Further reading
- •Appendix A Summary of linear algebra
- •Vector space
- •References
- •Index

74 |
|
Tensor analysis in special relativity |
|
|
|
|
|
Circular reasoning? |
|
|
|
|
|
|
At this point the student might worry that all of tensor algebra has become circular: oneforms were defined in terms of vectors, but now we have defined vectors in terms of one-forms. This ‘duality’ is at the heart of the theory, but is not circularity. It means
we can do as physicists do, which is to identify the vectors with displacements x |
||||
and things like it (such as p and v) and then generate all |
|
M |
|
|
|
N |
tensors by the rules of |
||
tensor algebra; these tensors inherit a physical meaning |
from the original meaning we |
|||
|
|
|
|
|
gave vectors. But we could equally well have associated one-forms with some physical objects (gradients, for example) and recovered the whole algebra from that starting point. The power of the mathematics is that it doesn’t need (or want) to say what the original vectors or one-forms are. It simply gives rules for manipulating them. The association of, say, p with a vector is at the interface between physics and mathematics: it is how we make a mathematical model of the physical world. A geometer does the same. He adds to the notion of these abstract tensor spaces the idea of what a vector in a curved space is. The modern geometer’s idea of a vector is something we shall learn about when we come to curved spaces. For now we will get some practice with tensors in physical situations, where we stick with our (admittedly imprecise) notion of vectors ‘like’ x.
3.7 I n d ex ‘ ra i s i n g ’ a n d ‘ l o w e r i n g ’
In the same way that the metric maps a vector V into a one-form V˜ , it maps an MN |
tensor |
|||||||||||||
mally, |
|
N 1 |
|
|
|
|
|
|
N |
|
|
N 1 |
|
|
into an |
|
M−1 |
tensor. Similarly, the inverse maps an |
M |
tensor into an |
|
M+1 |
|
|
|||||
|
|
+ |
|
|
|
|
|
|
|
|
|
− |
|
|
these are given the same name, and are distinguished only by the positions of their |
||||||||||||||
|
|
|
|
αβ |
components of a |
2 |
tensor. Then |
|
|
|
|
|||
indices. Suppose T |
γ are the |
|
α |
1 αμ |
|
|
|
|
|
|
||||
|
|
|
|
|
T |
βγ := ηβμT |
γ |
|
|
|
|
(3.56) |
||
are the components of a 12 tensor (obtained by mapping the second one-form argument of Tαβ γ into a vector), and
Tα β γ := ηαμTμβ γ |
(3.57) |
are the components of another (inequivalent) 12 tensor (mapping on the first index), while
Tαβγ := ηγ μTαβ μ |
(3.58) |
are the components of a 30 tensor. These operations are, naturally enough, called index ‘raising’ and ‘lowering’. Whenever we speak of raising or lowering an index we mean this map generated by the metric. The rule in SR is simple: when raising or lowering a ‘0’ index, the sign of the component changes; when raising or lowering a ‘1’ or ‘2’ or ‘3’ index (in general, an ‘i’ index) the component is unchanged.

75 |
3.7 Index ‘raising’ and ‘lowering’ |
Mixed components of metric
The numbers {ηαβ } are the components of the metric, and {ηαβ } those of its inverse. Suppose we raise an index of ηαβ using the inverse. Then we get the ‘mixed’ components of the metric,
ηα β ≡ ηαμημβ . |
(3.59) |
But on the right we have just the matrix product of two matrices that are the inverse of each other (readers who aren’t sure of this should verify the following equation by direct calculation), so it is the unit identity matrix. Since one index is up and one down, it is the Kronecker delta, written as
|
|
|
ηα β ≡ δα β . |
|
|
(3.60) |
|
|
|
|
|
||
By raising the other index |
we merely obtain an identity, ηαβ |
= |
ηαβ . So we can regard ηαβ |
|||
2 |
|
0 |
tensor g by g−1. So, for |
|||
as the components of the |
0 |
tensor, which is mapped from the |
2 |
|||
g, its ‘contravariant’ |
components equal the elements of the matrix inverse of the matrix of |
|||||
|
|
|
|
|
|
|
its ‘covariant’ components. It is the only tensor for which this is true.
Metric and nonmetric vector algebras
It is of some interest to ask why the metric is the one that generates the correspondence
between one-forms and vectors. Why not some other 02 tensor that has an inverse? We’ll explore that idea in stages.
First, why a correspondence at all? Suppose we had a ‘nonmetric’ vector algebra, com-
plete with all the dual spaces and MN tensors. Why make a correspondence between one-forms and vectors? The answer is that sometimes we do and sometimes we don’t. Without one, the inner product of two vectors is undefined, since numbers are produced only when one-forms act on vectors and vice-versa. In physics, scalar products are useful, so we need a metric. But there are some vector spaces in mathematical physics where metrics are not important. An example is phase space of classical and quantum mechanics.
Second, why the metric and not another tensor? If a metric were not defined but another symmetric tensor did the mapping, a mathematician would just call the other tensor the metric. That is, he would define it as the one generating a mapping. To a mathematician, the metric is an added bit of structure in the vector algebra. Different spaces in mathematics can have different metric structures. A Riemannian space is characterized by a metric that gives positive-definite magnitudes of vectors. One like ours, with indefinite sign, is called pseudo-Riemannian. We can even define a ‘metric’ that is antisymmetric: a two-dimensional space called spinor space has such a metric, and it turns out to be of fundamental importance in physics. But its structure is outside the scope of this book. The point here is that we don’t have SR if we just discuss vectors and tensors. We get SR when

76 |
Tensor analysis in special relativity |
we say that we have a metric with components ηαβ . If we assigned other components, we might get other spaces, in particular the curved spacetime of GR.
|
|
|
|
3.8 D i f f e re n t i a t i o n |
o f t e n s o r s |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
A function f is a |
0 |
tensor, and its gradient |
df is a |
0 |
tensor. Differentiation of a function |
|||
|
0 |
˜ |
|
|
1 |
|
|||
|
|
|
of one higher (covariant) rank. We shall now see that this applies as well |
||||||
|
produces a tensor |
|
|
|
|
|
|||
|
to differentiation of tensors of any rank. |
|
|
|
|
|
|||
|
Consider a |
1 |
tensor T whose components |
{ |
Tα |
are functions of position. We can |
|||
|
write T as |
1 |
|
T = Tα |
|
|
β } |
|
|
|
|
|
|
β ω˜ β eα . |
(3.61) |
||||
Suppose, as we did for functions, that we move along a world line with parameter τ , proper time. The rate of change of T,
dT |
= |
lim |
|
T(τ + τ ) − T(τ ) |
, |
(3.62) |
|
dτ |
0 |
|
|||||
τ |
→ |
τ |
|
||||
|
|
|
|
|
|
|
|
is not hard to calculate. Since the basis one-forms and vectors are the same everywhere
(i.e. ω˜ α (τ + τ ) = ω˜ α (τ )), it follows that |
|
|||||
dT |
|
dTα |
|
|||
|
|
= |
β |
ω˜ β eα , |
(3.63) |
|
|
dτ |
dτ |
||||
where dTα β /dτ is the ordinary derivative of the function Tα β along the world line: |
|
|||||
1 |
|
dTα β /dτ = Tα β,γ Uγ . |
(3.64) |
|||
|
tensor, since in Eq. (3.62) it is defined to be just the |
|||||
Now, the object dT/dτ is a 1 |
||||||
difference between two such tensors. From Eqs. (3.63) and (3.64) we have, for any
vector U,
|
|
|
|
dT/dτ = (Tα β,γ ω˜ β eα ) Uγ , |
(3.65) |
from which we can deduce that |
|
||||
|
|
|
|
T := (Tα β,γ ω˜ β ω˜ γ eα ) |
(3.66) |
is a |
˜ |
|
|||
1 |
|
tensor. This tensor is called the gradient of T. |
|
||
|
2 |
|
|
|
|
We use the notation T rather than dT because the latter notation is usually reserved by mathematicians for something else. We also have a convenient notation for Eq. (3.65):
dT/dτ = U T, |
(3.67) |
U T → Tα β,γ Uγ . |
(3.68) |
This derivation made use of the fact that the basis vectors (and therefore the basis oneforms) were constant everywhere. We will find that we can’t assume this in the curved spacetime of GR, and taking this into account will be our entry point into the theory !
77 |
3.10 Exercises |
3.9 F u r t h e r re a d i n g
Our approach to tensor analysis stresses the geometrical nature of tensors rather than the transformation properties of their components. Students who wish amplification of some of the points here can consult the early chapters of Misner et al. (1973) or Schutz (1980b). See also Bishop and Goldberg (1981).
Most introductions to tensors for physicists outside relativity confine themselves to ‘Cartesian’ tensors, i.e. to tensor components in three-dimensional Cartesian coordinates. See, for example, Bourne and Kendall (1991) or the chapter in Mathews and Walker (1965).
A very complete reference for tensor analysis in the older style based upon coordinate transformations is Schouten (1990). See also Yano (1955). Books which develop that point of view for tensors in relativity include Adler et al. (1975), Landau and Lifshitz (1962), and Stephani (2004).
3.10E xe rc i s e s
1(a) Given an arbitrary set of numbers {Mαβ ; α = 0, . . . , 3; β = 0, . . . , 3} and two arbitrary sets of vector components {Aμ, μ = 0, . . . , 3} and {Bν , ν = 0, . . . , 3}, show
that the two expressions
3 3
Mαβ Aα Bβ := Mαβ Aα Bβ α=0 β=0
and
3
Mαα Aα Bα
α=0
are not equivalent.
(b) Show that
Aα Bβ ηαβ = −A0B0 + A1B1 + A2B2 + A3B3.
2Prove that the set of all one-forms is a vector space.
3(a) Prove, by writing out all the terms, the validity of the following
|
|
|
˜ |
|
p˜(Aα eα ) = Aα p˜(eα ). |
|
|
|
− |
|
|
|
||||||||
(b) |
|
|
|
− |
|
|
|
|
|
|
A be (2, 1, 0, |
1) and those of B |
||||||||
|
Let the components of p be ( |
|
1, 1, 2, 0), those of |
˜ |
|
|
− |
˜ |
|
|||||||||||
|
|
|
˜ |
|
|
˜ |
|
|
˜ |
|
− |
|
|
|
|
|||||
|
|
|
|
A); (ii) p(B); (iii) p(A |
|
3B); (iv) p(A) |
|
|
|
3p(B). |
||||||||||
|
be (0, 2, 0, 0). Find (i) p( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 Given the following vectors in O: |
|
|
|
→ |
|
|
|
→ |
|
− |
|
|
|
|
||||||
|
→ |
|
→ (1, 2, 0, 0), |
|
|
( |
3, 2, 0, 0), |
|||||||||||||
|
A |
(2, 1, 1, 0), B |
O |
|
|
|
C |
O |
(0, 0, 1, 1), D |
O |
|
|
||||||||
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(a)show that they are linearly independent;
(b)find the components of p˜ if
78
Figure 3.5
Tensor analysis in special relativity
˜ |
= ˜ |
= − ˜ |
C) |
= − ˜ |
= |
0; |
p(A) |
1, p(B) |
|
1, p(D) |
|
||
|
1, p( |
|
|
|
||
(c)find the value of p(E) for
→ (1, 1, 0, 0);
E
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
O |
|
˜ |
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
˜ |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
A) |
|||||
(d) determine whether the one-forms p, q, r, and s are linearly independent if q( |
|
||||||||||||||||||||||||||||||||||
q(B) |
= |
0, q( |
|
= |
|
|
˜ |
|
|
= − ˜ |
|
|
|
|
= |
|
˜ |
|
= ˜ |
|
= ˜ |
|
= |
˜ |
|
= |
|||||||||
˜ |
|
|
˜ |
C) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
− |
˜ |
|
|
|
˜ |
1, q(D) |
|
= |
1, r(A) |
|
|
2, r(B) |
r(C) |
r(D) |
|
0, s(A) |
|
||||||||||||||||||
|
= − |
|
|
C) |
= ˜ |
|
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1, s(B) |
|
|
|
1, s( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 Justify each step leading from Eqs. (3.10a) to (3.10d). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
6 Consider the basis |
{ |
} |
of a frame |
O |
|
|
|
|
|
|
|
|
|
λ0 |
λ1 |
λ2 |
λ3 |
) for the space of |
|||||||||||||||||
|
eα |
|
|
and the basis (˜ |
, ˜ |
, ˜ |
, ˜ |
||||||||||||||||||||||||||||
one-forms, where we have |
|
|
|
|
˜ |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1, 1, 0, 0), |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ0 |
O |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
(1, |
1, 0, 0), |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ1 |
O |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
(0, 0, 1, |
1), |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ2 |
O |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
(0, 0, 1, 1). |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ3 |
O |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
{ |
|
} |
|
|
|
|
|
|
|
|
|
|
|
{ |
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note that |
λβ |
is not the basis dual to |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
e |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
˜ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(a)Show that p˜ = p˜(e )˜ α for arbitrary p˜.
αλ
(b)Let p˜ →O (1, 1, 1, 1). Find numbers lα such that
|
|
|
|
|
˜ = |
|
α |
˜ |
|
|
|
|
|
˜ |
{ |
|
p |
l |
|
λα . |
˜ |
||
|
|
|
} |
λα . |
|
|
|||||
|
These are the components of p on |
|
λα |
|
, which is to say that they are the values of p on |
||||||
|
|
˜ |
|
||||||||
7 |
the elements of the vector basis dual to {˜ |
} |
|
|
|
||||||
Prove Eq. (3.13). |
|
|
|
|
|
|
|
|
|
. |
|
8 |
dt and dx of a frame |
O |
|||||||||
Draw the basis one-forms ˜ |
˜ |
|
|
|
|
|
|
|
|
||
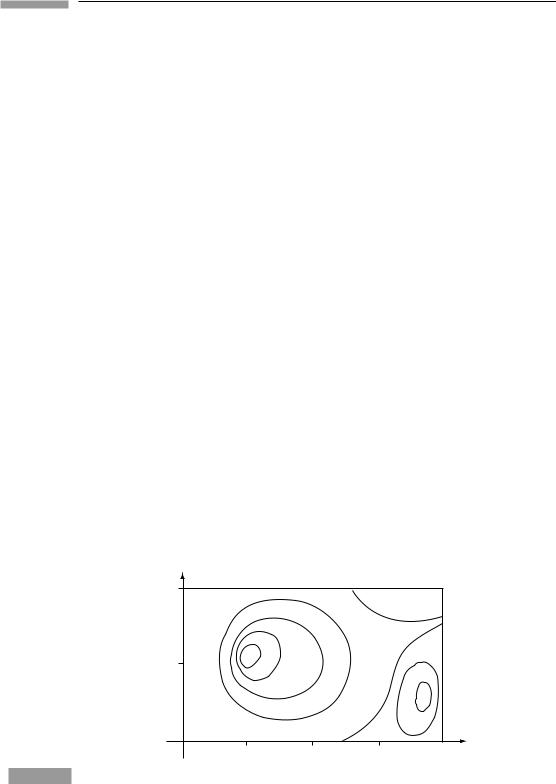
9 Fig. 3.5 shows curves of equal temperature T (isotherms) of a metal plate. At the points
P Q ˜
and as shown, estimate the components of the gradient dT. (Hint: the components
y |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
10 |
0 |
|
20 |
|
|
|
0 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
x |
|
|
Isotherms of an irregularly heated plate.

79 |
3.10 Exercises |
are the contractions with the basis vectors, which can be estimated by counting the number of isotherms crossed by the vectors.)
10(a) Given a frame O whose coordinates are {xα }, show that
∂xα /∂xβ = δα β .
(b)For any two frames, we have, Eq. (3.18):
∂xβ /∂xα¯ = β α¯ .
Show that (a) and the chain rule imply
β α¯ α¯ μ = δβ μ.
This is the inverse property again.
11Use the notation ∂φ/∂xα = φ,α to re-write Eqs. (3.14), (3.15), and (3.18).
12Let S be the two-dimensional plane x = 0 in three-dimensional Euclidean space. Let
n˜ =0 be a normal one-form to S. |
= |
||
(a) |
Show that if V |
˜ |
|
is a vector which is not tangent to S, then n(V) |
0. |
||
(b) |
˜ |
˜ |
|
Show that if n(V) > 0, then n(W) > 0 for any W, which points toward the same |
|||
x side of S as V does (i.e. any W whose x components has the same sign as V ).
(c)Show that any normal to S is a multiple of n˜.
(d)Generalize these statements to an arbitrary three-dimensional surface in fourdimensional spacetime.
13 |
|
|
df |
is normal to surfaces of constant f . |
Prove, by geometric or algebraic arguments, that ˜ |
|
|||
14 |
Let p˜ →O (1, 1, 0, 0) and q˜ →O (−1, 0, 1, 0) be two one-forms. Prove, by trying two |
|||
|
vectors |
|
˜ ˜ = ˜ ˜ |
˜ ˜ |
|
A and B as arguments, that p q q p. Then find the components of p q. |
|||
15Supply the reasoning leading from Eq. (3.23) to Eq. (3.24).
16(a) Prove that h(s) defined by
h(s)(A, B)
is an symmetric tensor.
(b) Prove that h(A) defined by
= 2 h( |
+ 2 |
|
|
|
1 |
A, B) |
1 h(B, A) |
(3.69) |
|
|
(A) |
|
= 2 |
|
− 2 h(B |
, |
|
h |
|
(A, B) |
1 h(A, B) |
1 |
A) |
(3.70) |
|
is an antisymmetric tensor.
(c) Find the components of the symmetric and antisymmetric parts of p˜ q˜ defined in
Exer. 14.
(d) Prove that if h is an antisymmetric 02 tensor,
|
A. |
|
|
|
|
|
|
|
for any vector |
|
|
|
|
|
|
(e) |
Find the number of independent components h(s) and h(A) have. |
|
|||||
17 (a) |
Suppose that h is a |
0 |
tensor with the property that, for any two vectors A and B |
||||
|
(where B =0) |
2 |
h( , |
= |
|
|
|
|
|
|
αh( |
|
|
||
|
|
|
A) |
|
, B), |
|
|

80 |
|
|
|
|
Tensor analysis in special relativity |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A and B. Show that there exist one- |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
where α is a number which may depend on |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
forms p˜ and q˜ such that |
|
h = p˜ q˜. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(b) |
Suppose T is a 11 tensor, ω˜ a one-form, v a vector, and T(ω˜ ; v) the value of T on |
||||||||||||||||
|
|
|
ω and v. Prove that T( ; v) is a vector and T(ω; |
) is a one-form, i.e. that a 1 |
|
||||||||||||||
|
|
|
˜ |
|
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
1 |
|
|
18 (a) |
tensor provides a map of vectors to vectors and one-forms to one-forms. |
|
||||||||||||||||
|
Find the one-forms mapped by the metric tensor from the vectors |
|
|
|
|
||||||||||||||
|
|
|
|
A |
(1, 0, |
− |
1, 0), |
B |
|
(0, 1, 1, 0), |
C |
|
( |
− |
1, 0, |
− |
1, 0), |
|
|
|
|
|
|
→O |
|
|
→O |
|
→O |
|
|
|
|
|
|||||
|
|
|
|
D→O(0, 0, 1, 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(b) |
Find |
the vectors |
mapped |
by |
the inverse |
of the |
metric |
tensor |
from |
||||||||
|
|
|
the one-form |
p˜ →O (3, 0, −1, −1), q˜ →O (1, −1, 1, 1), |
r˜ →O (0, −5, −1, 0), |
||||||||||||||
|
|
|
s˜ →O (−2, 1, 0, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
19(a) Prove that the matrix {ηαβ } is inverse to {ηαβ } by performing the matrix multiplication.
(b)Derive Eq. (3.53).
20In Euclidean three-space in Cartesian coordinates, we don’t normally distinguish between vectors and one-forms, because their components transform identically. Prove this in two steps.
(a)Show that
Aα¯ = α¯ β Aβ
and
P ¯ = α ¯ Pα
β β
are the same transformation if the matrix { α¯ β } equals the transpose of its inverse. Such a matrix is said to be orthogonal.
(b)The metric of such a space has components {δij, i, j = 1, . . . , 3}. Prove that a transformation from one Cartesian coordinate system to another must obey
δ = k¯ l¯δkl ij i j
and that this implies { k¯i} is an orthogonal matrix. See Exer. 32 for the analog of this in SR.
21(a) Let a region of the t − x plane be bounded by the lines t = 0, t = 1, x = 0, x = 1. Within the t − x plane, find the unit outward normal one-forms and their associated
vectors for each of the boundary lines.
(b)Let another region be bounded by the straight lines joining the events whose coordinates are (1, 0), (1, 1), and (2, 1). Find an outward normal for the null boundary and find its associated vector.
22Suppose that instead of defining vectors first, we had begun by defining one-forms, aided by pictures like Fig. 3.4. Then we could have introduced vectors as linear realvalued functions of one-forms, and defined vector algebra by the analogs of Eqs. (3.6a) and (3.6b) (i.e. by exchanging arrows for tildes). Prove that, so defined, vectors form a vector space. This is another example of the duality between vectors and one-forms.

81 |
3.10 Exercises |
23(a) Prove that the set of all MN tensors for fixed M, N forms a vector space. (You must define addition of such tensors and their multiplication by numbers.)
(b)Prove that a basis for this space is the set
{eα eβ · · · eγ
|
|
|
|
|
|
M |
|
|
|||
|
|
vectors |
|
||
ω˜ μ ω˜ ν · · · ω˜ λ}.
N one-forms
(You will have to define the outer product of more than two one-forms.)
24 (a) Given the components of a 20 tensor Mαβ as the matrix
0 1 0 0
1 −1 0 2
,
2 0 0 1
1 0 −2 0
find:
(i)the components of the symmetric tensor M(αβ) and the antisymmetric tensor
M[αβ];
(ii)the components of Mα β ;
(iii)the components of Mα β ;
(iv)the components of Mαβ .
(b)For the 11 tensor whose components are Mα β , does it make sense to speak of its symmetric and antisymmetric parts? If so, define them. If not, say why.
(c)Raise an index of the metric tensor to prove
|
|
|
|
|
|
ηα β = δα β . |
|
|
|
||
25 Show that if A is a 2 |
|
|
|
|
0 |
tensor, then |
|
|
|
||
|
0 tensor and B a 2 αβ |
Bαβ |
|
|
|
||||||
|
|
|
|
|
|
A |
|
|
|
|
|
is frame invariant, i.e. a scalar. |
2 |
|
|
|
|
0 |
|
0 |
|||
26 Suppose A is an antisymmetric |
|
tensor, B a symmetric |
tensor, C an arbitrary |
||||||||
|
|
|
|
0 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
tensor, and D an arbitrary |
2 |
tensor. Prove: |
|
||||||||
0 |
|
|
|
|
|
|
|
||||
(a) |
Aαβ Bαβ = 0; |
|
|
|
|
|
|
|
|
|
|
(b) |
Aαβ Cαβ = Aαβ C[αβ]; |
|
|
|
|
|
|
|
|
|
|
(c) |
Bαβ Dαβ = Bαβ D(αβ). |
|
|
|
|
|
|
|
|
|
|
27 (a) Suppose A is an antisymmetric 20 tensor. Show that {Aαβ }, obtained by lowering indices by using the metric tensor, are components of an antisymmetric
(b) Suppose Vα = Wα . Prove that Vα = Wα .
28Deduce Eq. (3.66) from Eq. (3.65).
29Prove that tensor differentiation obeys the Leibniz (product) rule:
(A B) = ( A) B + A B.
O
30 In some frame , the vector fields U and D have the components:
|
→ |
(1 |
+ |
t2, t2, |
√2 t, 0), |
U |
→ |
|
|||
|
(x, 5 tx, √2 t, 0), |
||||
D |
|
||||
82 |
|
|
|
|
|
Tensor analysis in special relativity |
|
|
|
|
|
|
|
|
|
|
|
and the scalar ρ has the value |
|||||
|
|
||||||
|
|
|
|
|
|
|
ρ = x2 + t2 − y2. |
|
|
(a) |
Find U · U, U · D, D · D. Is U suitable as a four-velocity field? Is D? |
||||
|
|
(b) |
Find the spatial velocity υ of a particle whose four-velocity is U, for arbitrary t. |
||||
|
|
|
What happens to it in the limits t → 0, t → ∞? |
||||
|
|
(c) |
Find Uα for all α. |
|
|||
|
|
(d) |
Find Uα ,β for all α, β. |
|
|||
|
|
(e) |
Show that Uα Uα ,β = 0 for all β. Show that Uα Uα,β = 0 for all β. |
||||
|
|
(f) |
Find Dβ ,β . |
|
|
|
|
|
|
(g) |
Find (Uα Dβ ),β for all α. |
||||
|
|
(h) |
Find Uα (Uα Dβ ),β and compare with (f) above. Why are the two answers similar? |
||||
|
|
(i) |
Find ρ,α for all α. Find ρ,α for all α. (Recall that ρ,α := ηαβ ρ,β .) What are the |
||||
|
|
|
numbers {ρ,α } the components of? |
||||
|
|
(j) |
Find |
|
|
|
|
|
|
U ρ, |
U D, |
Dρ, |
DU. |
||
|
31 Consider a timelike unit four-vector U, and the tensor P whose components are |
||||||
|
|
given by |
|
|
|
|
|
|
|
|
|
|
|
|
Pμν = ημν + UμUν . |
|
|
(a) |
Show that P is a projection operator that projects an arbitrary vector V into one |
||||
|
|
|
orthogonal to U. That is, show that the vector V whose components are |
||||
Vα = Pα β Vβ = (ηα β + Uα Uβ )Vβ
is
(i) orthogonal to U, and
(ii) unaffected by P:
Vα := Pα β Vβ = Vα .
(b)Show that for an arbitrary non-null vector q, the tensor that projects orthogonally to it has components
ημν − qμqν /(qα qα ).
How does this fail for null vectors? How does this relate to the definition of P?
(c) Show that P defined above is the metric tensor for vectors perpendicular to U:
=
P(V ,W ) g(V ,W )
= ·
V W .
32(a) From the definition fαβ = f(eα , eβ ) for the components of a 02 tensor, prove that the transformation law is
fαβ |
μα ν |
β fμν |
¯ ¯ = |
¯ |
¯ |
and that the matrix version of this is
(¯ |
= |
( )T (f )( ), |
f ) |
|
where ( ) is the matrix with components μα¯ .

83 |
3.10 Exercises |
(b)Since our definition of a Lorentz frame led us to deduce that the metric tensor has
components ηαβ , this must be true in all Lorentz frames. We are thus led to a more general definition of a Lorentz transformation as one whose matrix μα¯ satisfies
η |
¯ ¯ = |
μα ν |
¯ |
ημν . |
|
¯ |
|
||
|
αβ |
|
β |
|
Prove that the matrix for a boost of velocity υ ex definition includes our older one.
(3.71)
satisfies this, so that this new
(c)Suppose ( ) and (L) are two matrices which satisfy Eq. (3.71), i.e. (η) = ( )T (η)( ) and similarly for (L). Prove that ( )(L) is also the matrix of a Lorentz
transformation.
33The result of Exer. 32c establishes that Lorentz transformations form a group, represented by multiplication of their matrices. This is called the Lorentz group, denoted by L(4) or 0(1,3).
(a)Find the matrices of the identity element of the Lorentz group and of the element inverse to that whose matrix is implicit in Eq. (1.12).
(b)Prove that the determinant of any matrix representing a Lorentz transformation is ±1.
(c)Prove that those elements whose matrices have determinant +1 form a subgroup, while those with −1 do not.
(d)The three-dimensional orthogonal group O(3) is the analogous group for the metric of three-dimensional Euclidean space. In Exer. 20b, we saw that it was represented by the orthogonal matrices. Show that the orthogonal matrices do form a group, and then show that 0(3) is (isomorphic to) a subgroup of L(4).
34Consider the coordinates u = t − x, v = t + x in Minkowski space.
(a) Define eu to be the vector connecting the events |
with |
coordinates |
{u = 1, |
v = 0, y = 0, z = 0} and {u = 0, v = 0, y = 0, z = 0}, |
and |
analogously |
for eν . |
Show that eu = (et − ex)/2, ev = (et + ex)/2, and draw eu and ev in a spacetime diagram of the t − x plane.
(b)Show that {eu , ev , ey, ez} are a basis for vectors in Minkowski space.
(c)Find the components of the metric tensor on this basis.
(d)Show that eu and ev are null and not orthogonal. (They are called a null basis for the t − x plane.)
|
|
|
, |
|
|
, |
) in terms of dt and dx. |
|
du, dv, g(e |
|
), g(e |
|
|||||
(e) Compute the four one-forms ˜ ˜ |
|
u |
|
|
v |
|
˜ |
˜ |
