2.10. Общая схема исследования функции. Построение графика

При общем исследовании функции полезно придерживаться следующего плана.

1. Элементарное исследование: область определения, симметрия графика (четность, нечетность), точки пересечения с осями координат (если это возможно).

2. Точки разрыва функции, вертикальные и наклонные асимптоты (исследование поведения функции на бесконечности).

3. Интервалы монотонности, точки экстремума (используя знаки ).

4. Точки перегиба, интервалы выпуклости и вогнутости (с помощью ).

5. Построение графика функции (основываясь на результатах исследования).

Пример 1.

Исследовать функцию и построить ее график.

1⁰. Функция определена на всей числовой оси, за исключением точкиx= 1, где знаменатель обращается в нуль. Так как область определения не симметрична относительно начала координат, то нет смысла говорить о четности (нечетности) функции.

Найдем точки пересечения графика с осями координат: y = 0 при x = 3 (точка пересечения с осью 0X); приx= 0y= 9 (точка пересечения с осью0Y).

2⁰. В точкеx=1 знаменатель дроби равен нулю, т.е.x= 1 – точка разрыва функции, а.

Точка x= 1 – точка бесконечного разрыва (II рода) и прямаяx= 1 является вертикальной асимптотой графика.

Найдем наклонную асимптоту y=kx+b:

.

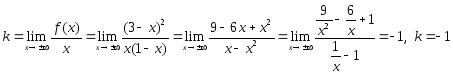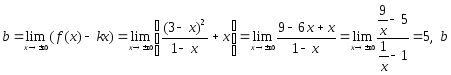=5.

Итак, наклонная асимптота y= 5 –x.

3⁰. Исследование функции с помощью первой производной:

.

при – стационарные точки,не существует приx=1 (в точке разрыва функции).

Отметим на числовой оси стационарные точки, точки разрыва функции и производной. Эти точки отделяют интервалы монотонности функции. Определим знаки в каждом из этих интервалов.

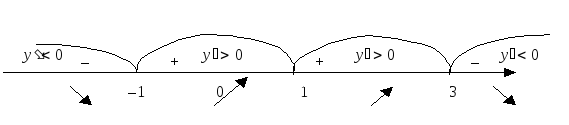
На интервалах , значит, функцияy(x) здесь убывает; на интервалах (–1, 1) и (1, 3) производная , следовательно, эти интервалы являются интервалами возрастания функции.

При переходе слева направо через точку x= –1 производнаяменяет знак с (–) на (+), следовательно,x=–1 – точка минимума,; при переходе через точкуx= 1 производная неменяет знака; при переходе же через точку x = 3 производная меняет знак с (+) на (–), значит, x = 3 – точка максимума,.

4⁰. Вычислим вторую производную:

.

Вторая производная в нуль не обращается, точек перегиба график не имеет. На интервале вторая производная положительна, график функции выпуклый. На интервалеграфик функции вогнутый.

Точка разрыва функции x= 1 отделяет выпуклую часть графика функции от вогнутой.

5⁰. График функции, построенный по результатам исследования, изображен на рис. 23.

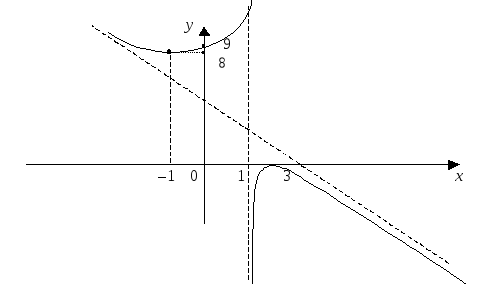
Рис. 23

3. Элементы интегрального исчисления

3.1. Понятие первообразной. Основные правила интегрирования

В предыдущей главе “Дифференциальное исчисление” мы решали следующую задачу: по данной функции найти ее производную. Во многих вопросах науки и техники приходится решать обратную задачу, а именно, восстанавливать функцию по известной ее производной. Эта обратная операция более сложная, чем предыдущая прямая задача.

Пусть дана функция f(x), которая является производной функцииF(x), и, зная функциюf(x), будем искатьF(x),для которойf(x) служит производной.

Определение.ФункцияF(x) называетсяпервообразнойфункцией для функцииf(x), еслиf(x) является производной дляF(x) или, что то же, выражениеf(x)dxслужит дифференциалом дляF(x) на данном промежутке измененияx:

или dF(x)=f(x)dx.

Так, например, для функции первообразной будет, так как.

Задача отыскания по данной функции ее первообразной решается неоднозначно. Например, есть первообразная для, так как. Но функциятакже будет первообразной для, так как. Вообще, любая функция, гдеc– произвольная постоянная, имеет производнуюи потому будет первообразной для.

Задача отыскания всех первообразных для f(x) является одной из основных задач интегрального исчисления.

Возникают три вопроса: всякая ли функция f(x) имеет первообразную? если первообразная существует, то единственна ли она? как находить первообразную?

На второй вопрос мы уже можем ответить. Справедливо следующее утверждение: если функция F(x) есть первообразная дляf(x) на некотором промежутке измененияx, тоF(x)+c, гдеc– любая постоянная, также будет первообразной. И обратно, каждая первообразная дляf(x) может быть представлена в видеF(x)+c. Таким образом, выражениеF(x)+cпредставляет собой общий вид первообразных дляf(x).

Совокупность всех первообразных для f(x) называется неопределенным интегралом функцииf(x) и обозначается

.

Операцию отыскания всех первообразных для f(x), т.е. отыскание неопределенного интеграла, называютинтегрированием функции f(x); функциюf(x) называютподынтегральной функцией, а выражениеf(x)dx–подынтегральным выражением.

Для ответа на второй вопрос сформулируем теорему, дающую достаточное условие интегрируемости функции на интервале.

Теорема.Если функцияf(x) непрерывна на данном промежутке, то она имеет на этом промежутке первообразную, т.е. существует.

Это утверждение мы примем без доказательства. Заметим только, что условие непрерывности не является необходимым для интегрируемости функции (например, функции, имеющие конечное число точек разрыва I рода на промежутке, также имеют первообразную). Ответ на вопрос, как найти первообразную для функции f(x), не прост. Начнем с того, что перечислим основные свойства неопределенного интеграла, или простейшие правила интегрирования.

1. , т.е.или.

2. или.

Выполнение этих свойств следует непосредственно из определения неопределенного интеграла и первообразной.

Свойства 1, 2 показывают, что если функцию f(x) проинтегрировать, а затем продифферен-цировать, то получим снова функциюf(x) .

Если к F(x) сначала применить операцию дифференцирования, а затем интегрирования, то получим сноваF(x), правда, следует прибавить к ней постояннуюc. Операции интегрирования и дифференцирования являются взаимно обратными.

3. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов, т.е.

.

4. Постоянный множитель можно выносить за знак интеграла

Для проверки всех этих простейших правил интегрирования достаточно продифференцировать обе части равенства.