1.6. Основные свойства бесконечно малых

1. Сумма конечного числа бесконечно малых функций при есть функция бесконечно малая при .

2. Произведение постоянной на функцию бесконечно малую при есть функция бесконечно малая при .

3. Произведение ограниченной функции на бесконечно малую при есть бесконечно малая функция при .

4. Произведение конечного числа бесконечно малых функций при есть функция бесконечно малая при .

1.7. Сравнение бесконечно малых. Эквивалентные бесконечно малые

Рассмотрим бесконечно малые (б.м.) функции при . Для краткости будем обозначать эти функции простоz. β, γ. Часто сравнивают б.м. функции по “быстроте” стремления к нулю. Если, то говорят, что α – б.м. более высокого порядка малости, чемβ. Обозначают так:. Например, функцияесть б.м. более высокого порядка, чемпри , так как. Если же, то говорят, чтоαиβ– эквивалентные бесконечно малые величины. Записывают так:α~β.

1.8. Бесконечно большие функции

Функция бесконечнобольшаяпри , т.е., если для любого сколь угодно большого числаМ> 0 найдется такое число, что для всехх, попадающих в окрестность,.

Функция бесконечно большая при , т.е., если для любого сколь угодно большого числаM>0 найдется такое числоN>0, что для всехxтаких, что, выполняется неравенство.

Всякая бесконечно большая функция является неограниченной, но не каждая неограниченная функция является бесконечно большой. Так, например, функция у=хsinхпри неограничена, но, предел этой функции при не существует.

Легко показать, что функция, обратная бесконечно малой, есть бесконечено большая и, наоборот, величина, обратная бесконечно большой, есть бесконечно малая.

1.9. Связь предела и бесконечно малых

Функцию, имеющую предел, можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины.

Действительно, если , тогда для всехх, достаточно близких к,,где ε – как угодно малая положительная величина, а это значит, что функция есть б.м. Следовательно,, где– б.м.

Верно и обратное утверждение. Если функцию можно представить как сумму постоянной и бесконечно малой величины, то это постоянное слагаемое есть предел функции, т.е. если , где– б.м. при , то.

1.10. Правила предельного перехода

Существуют правила, при помощи которых часто удается непосредственно находить пределы функций. Сформулируем простейшие из этих правил.

1. Предел постоянной функции равен самой постоянной.

Пусть f(x) =c, тогда можно представить функцию как сумму, где, т.е..

2. Предел суммы, разности, произведения конечного числа функций, имеющих предел при (или при ), равен соответственно сумме, разности, произведению пределов этих функций.

Если ,, то,.

Предел частного двух функций равен частному их пределов, если предел знаменателя не равен нулю.

Если ,, то.

Докажем одно из этих утверждений, например, предел произведения. Пусть ,, это значит, что, а, гдеипри , а произведение функций.

Величина, заключенная в скобки, есть бесконечно малая при , а поэтому

Подобным образом можно доказать это утверждение в случае любого конечного числа множителей.

Остальные утверждения доказываются аналогично.

Из изложенных утверждений, в частности, следуют:

Следствие 1.Постоянный множитель можно выносить за знак предела:

Следствие 2.Предел степени равен степени от предела:

Заметим, что это правило верно не только для целых положительных степеней n, но для любого.

Изложенные здесь утверждения дают простые правила для нахождения пределов. Пользуясь этим правилами, решим следующие примеры.

Пример 1.Найдем предел функциипри .

Имеем

Пример 2..

Пример 3..

Здесь и числитель и знаменатель – бесконечно малые, но их можно представить в виде ,.

Теперь получим

Пример 4..

Воспользоваться непосредственно теоремой о пределе частного здесь нельзя, так как предел знаменателя равен нулю. Предварительно преобразуем функцию

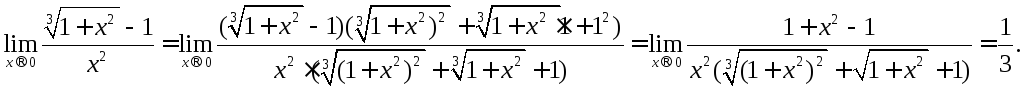
Здесь использовано разложение (a³–b³) = (a–b) (a²+ab+b²).

К функции уже можно применить правило о пределе частного.

Не будем более останавливаться на технике вычисления пределов. Заметим, что при вычислении пределов возникают неопределенности следующих типов: , требующие дополнительных преобразований. В то же время, как уже было отмечено ранее, величина, обратная бесконечно малой, стремится к бесконечности. Например,.

Величина, обратная бесконечно большой , есть бесконечно малая величина. Например,.

Итак, величины типа ине являются неопределенностями. Для раскрытия перечисленных ранее неопределенностей используются следующие замечательные пределы.

1. Предел отношения многочленов при стремлении аргумента к бесконечности (неопределен-ность типа ):

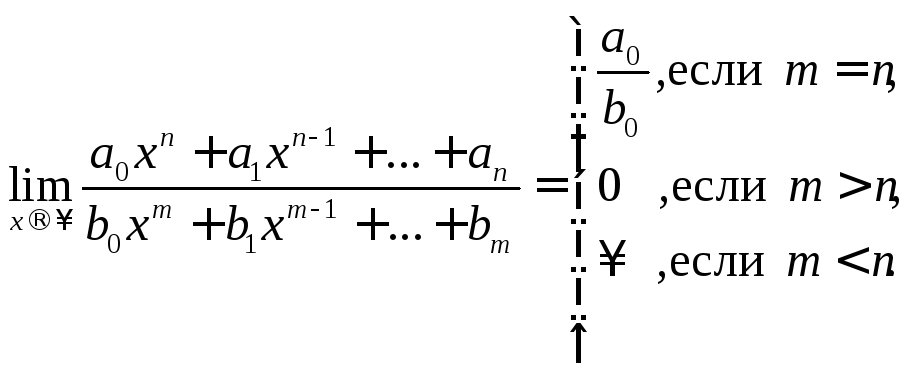
Убедимся в справедливости этой формулы.

Пример 5.

.

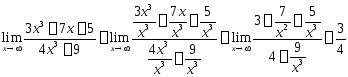Здесь мы использовали тот факт, что

В этом примере степени многочленов в числителе и знаменателе равны m = n =3, . Формула верна.

Пример 6.

, здесь m = 4, n = 3 (m > n).

2. Предел отношения :(I замечательный предел).

Отсюда следует, что функция и ее аргумент α эквивалентные бесконечно малые при любом.

Пример 7.

.

Пример 8.

так как

Следует иметь в виду, что предел функции при ,отличен от единицы. Так, например,.

3. (II замечательный предел).

Если в этом равенстве положить (при х→∞, α→0), то оно запишется в виде

Пример 9.

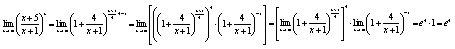
Вычисление пределов произведения (частного) может упроститься, если заменить бесконечно малую величину ей эквивалентной. Выпишем некоторыe эквивалентныe бесконечно малых.

1
2
3
4

Пример 10.