3.2. Основные методы интегрирования

Мы уже начали обсуждение методов интегрирования, сформулировав простейшие правила вычисления интегралов. Как уже говорилось, вычислениe неопределенного интеграла является задачей значительно более трудной, чем отыскание производной. Например, нет никаких правил для интегрирования произведения или частного двух функций. Кроме того, интегралы от некоторых элементарных функций не являются элементарными функциями. Например, и другие не берутся в элементарных функциях.

Мы выпишем здесь таблицу основных интегралов и научимся сводить вычисление некоторых интегралов к табличным.

Таблица

Основных интегралов (c – постоянная)

1
2
3
4
5
6
7
8
9
10
11

Заметим, что переменная интегрирования может быть любой: . Часто удается введением новой переменной интегрирования свести интегралк более простому, например, табличному. Имеет место формула замены переменной в неопределенном интеграле:, где– непрерывная монотонная функция, имеющая непрерывную производную.

Пример 1.Вычислить.

Введем новую переменную t= 1–9x, или.

Вычислим и подставим в интеграл:

.

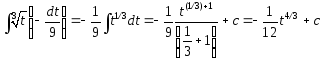Возвращаясь к переменной x, получим

.

Пример 2.Вычислить.

Сделаем замену переменной xнаt:, подставляем в интеграл:.

Но интеграл – табличный, поэтому.

Рассмотренные примеры можно решить, применяя следующее правило: если , то, гдеa,b,c– постоянные.

Пример 3.Вычислить, гдеa= –5,b= 2. Табличный интеграл, здесь, тогда.

Пример 4.Вычислить.

Введем новую переменную . Здесь, в отличие от предыдущего примера, заменапеременной не является линейной. Тогда dt=2xdx, и.

Метод, рассмотренный в примерах 1-4, называют методом подстановки.

Следующий метод, который мы здесь рассмотрим, называют интегрированием по частям.

Приведем правило интегрирования по частям.

Пусть мы имеем интеграл , где подынтегральное выражение представляет собой произведение некоторой функцииu(x) на дифференциал другой функции, т.е., гдеu(x) ипредполагаются непрерывно дифференцируемыми.

Тогда имеет место формула или, коротко,.

Рассмотрим на примерах, как применяется формула интегрирования по частям.

Пример 5.Вычислить.

Пусть u=х,. Найдемdu, υ и подставим в формулу

.

Пример 6.Найти.

Пусть . Тогда:.

Имеется целый класс функций, интегралы от которых вычисляются именно с помощью интегрирования по частям. Например, и другие.

Рассмотрим еще один класс функций, для которых интегралы вычисляются и являются элементарными функциями. Речь идет о рациональных функциях, которые представляются отношением двух многочленов. Напомним, что многочленом степени nназывается функция вида, где.

Степенью многочлена считается старшая степень переменной x, входящей в многочлен. Так, многочленявляется многочленом степениn= 4.

Рациональной функцией, или рациональной дробью, называется функция , равная отношению двух многочленов. Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена в знаменателе, т.е.R(x) – правильная дробь, еслиn<m.

Всякая неправильная рациональная дробь может быть представлена (простым делением числителя на знаменатель) в виде суммы многочлена и правильной дроби. Например,

Так как интегрирование целой части (3x–3) не представляет трудностей, то достаточно показать, как интегрируются правильные рациональные дроби, здесь.

К простейшим правильным рациональным дробям относятся следующие типы дробей:

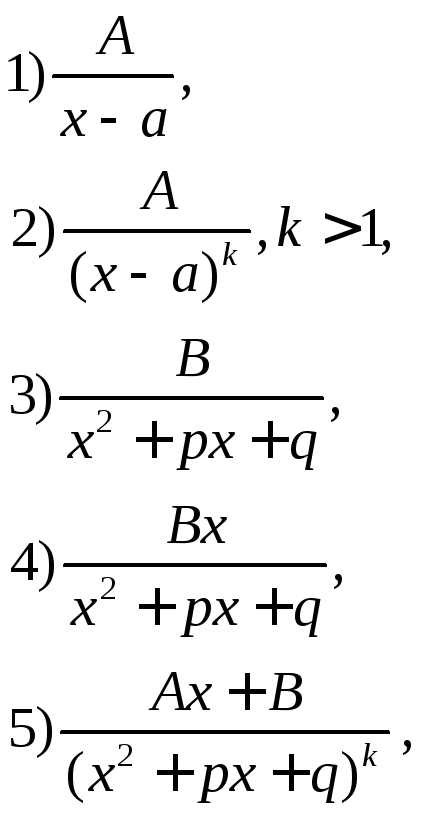
причем в дробях 3-5 квадратный трехчлен не имеет вещественных корней, т.е. дискриминант .

Справедлива следующая теорема.

Теорема.Правильная дробьR(x) допускает представление в виде суммы простейших дробей.

Так, например, покажем, что , и найдем интеграл.

Пример 7..

Подберем AиBтак, чтобы равенство выполнялось при любых значенияхx:

,

т.е. .

Так как знаменатели в последнем равенстве одинаковые, то должны быть равны и числители

(*)

при всех значениях x. Положим в равенстве (*)х= 0, получимА = –1, затем прих= –1 имеем –В= 5(–1)–1.

Итак, A=–1,B= 6, а дробь; интегрируя, получим:

.

Пример 8.Вычислить.

Применим тот же общий прием: представим подынтегральную функцию как сумму простейших дробей

.

Знаменатели самой левой дроби и самой правой совпадают. Для равенства дробей потребуем, чтобы совпадали и числители при всяком значении x:x + 3 =Вx + (A + 2B).

Последнее равенство возможно, если равны коэффициенты при одинаковых степенях переменной x, т.е.B = 1,A + 2B = 3. ОткудаA = 1 и

.

Пример 9.Вычислить интеграл от простейшей дроби.

Для этого сначала в знаменателе выделим полный квадрат:

.

Замена переменной t =x + 2,dt =dxсводит наш интеграл к табличному:

.

Мы обсудили в этом параграфе только некоторые приемы вычисления неопределенного интеграла (сведение интеграла к табличному, простейшие замены переменной, интегрирование по частям, интегрирование рациональных дробей). Изучение многих других приемов интегрирования не входит в нашу задачу.