2. Дифференциальное исчисление функций одной переменной

2.1. Производная функции. Ее геометрический смысл

Определение. Производной функции y=f(x) в точке называется предел отношения приращения функциик приращению аргумента при стремлении последнего к нулю.

Обозначение:

.

Для производной в точке x₀можно использовать и другие обозначения:.

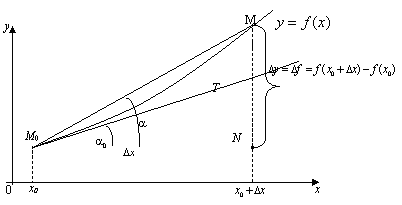
Поясним понятие производной геометрически. На рис. 13 видно, что , а отрезок, из треугольникаполучаем, здесь α – угол наклона секущейк осиОX. Присекущаястремится занять положение касательнойТ, составляющей уголс осью абсцисс – угол наклона касательной. При этом. Следовательно,, т.е. производная есть тангенс угла наклона касательной, илиравен угловому коэффициенту касательной, проведенной к графику функциив точке.

Рис. 13

Напомним, что уравнение прямой, проходящей через точку и имеющей угловой коэффициентk, имеет вид.

Поскольку , то уравнение касательной запишется так:.

2.2. Дифференциал функции, его геометрический смысл

Напомним, что если , то в окрестностиимеем, где(при ). Из определения производной следует, что, где при , т.е. - б.м. при . Отсюда.

Приращение функции представляет собой сумму двух слагаемых:– есть бесконечно малая более высокого порядка, чем(вспомните, что это значит); второе слагаемоелинейно зависит оти служит хорошим приближением к приращению функциипри малых.

Определение.Величинаназываетсядифференциалом функции f(x) в точке и обозначается.

Таким образом,

. (*).

Такое выражение для возможно лишь в случае существования. Подобные функции называют дифференцируемыми в точке. Формулу (*) можно использовать в приближенных вычислениях. Из определения следует, что для независимой переменнойи.

Геометрический смысл дифференциала виден из рис. 14.

Из имеем:, но,. Следовательно,. Поэтому говорят, чтоdfесть приращение ординаты касательной (т.е. приращение линейной функции, графиком которой служит касательная). На рисунке отличиеdfотвыглядит величиной, сравнимой си. Но это потому, что величинане мала. При видно, что отличие начинает “сильно проигрывать” приращениюи действительно является величиной, стремящейся к нулю быстрее, чем(т.е.о).

Рис. 14

В приближенных вычислениях полагают , или

2.3. Общее представление о линеаризации функции

При изучении функции вблизи какой-либо точки, например вблизи нуля, часто бывает выгодно заменить исследуемую функцию другой, более удобной для рассмотрения функцией, например линейной. При этом допускается некоторая ошибка.

Пусть задана функция . Вблизи нуляхмало, аеще меньше, и последний член не оказывает существенного влияния на поведение данной функции. Если отбросить член, функция заменится линейной:. Этот процесс замены функции линейной функцией называетсялинеаризацией. При линеаризации многочлена вблизи нуля отбрасываются все члены, содержащие степениxвыше первой.

Пример1., отсюда следует: если, то.

Если , то.

Особенно важен случай .

Здесь отброшенные члены являются бесконечно малыми более высокого порядка, чем x, т.е..

Можно доказать, что , т.е.. Выписанные ранее эквивалентные величины позволяют нам заменить некоторые функции вблизи нуля более простыми, линейными функциями, т.е. линеаризовать их. Таким образом, мы имеем:

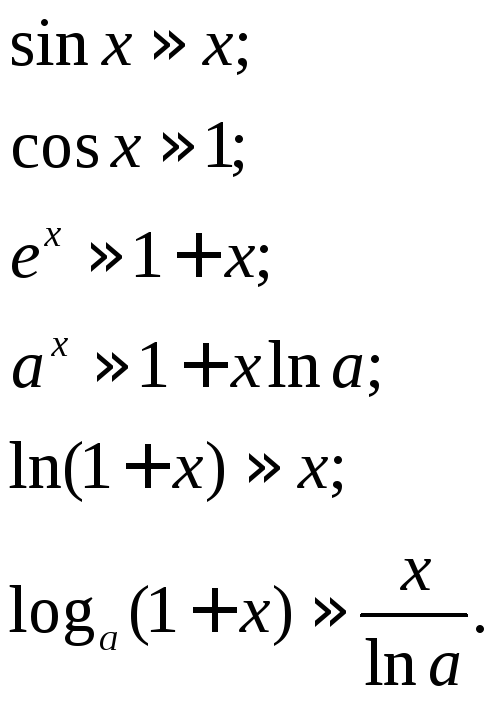
Погрешности, получаемые при такой замене, есть бесконечно малые более высокого порядка малости, чем x, т.е. o(x). Заметим, что функцииинельзя линеаризовать вблизи нуля, так как вблизиx= 0 они не ограничены.

Пример 2.Пусть необходимо приближенно вычислить. Представим число 82 в виде суммы 81+1. Тогда

При линеаризации функции y=f(x) вблизи точки, т.е. при, величина приращения аргументабудет бесконечно малой. Функциюf(x), если это возможно, представляют в виде

или

.

Мы знаем, что величина является дифференциалом функцииy=f(x), т.е..

Итак, функции, допускающие линеаризацию, являются дифференцируемыми. Процесс линеаризации функции эквивалентен замене приращения функции вблизи точки ее дифференциалом:

или

.

Например:

1⁰.. Имеем, значит,

.

В частности, при x= 0; так,

.

2⁰.y= lnx. Имеем, значит,.

В частности, при x= 1 получаем знакомую формулу(при ); так, ln 1,03≈0,03.

Из геометрического смысла дифференциала следует, что линеаризация функции y=f(x) вблизи точкиозначает замену графика функции куском ее касательной в этой точке. Эта идея используется при отыскании интегральной кривой дифференциального уравнения. Подробнее об этом будет сказано ниже.