1.3. Предел функции

Перейдем к понятию предела функции у=f(x) непрерывного аргументах.

Пусть функция f(x) определена в некоторой окрестности точки, т.е. в некотором интервале, содержащем точку, кроме, быть может, самой точки. В точкефункция может быть и не определена. ЧислоAназываетсяпределом функции f(x) при стремлении x к х₀ , если для любого положительного числанайдется такое положительное число, что для всехх, удовлетворяющих условию, выполняется неравенство.

Записывают: или.

Это можно следующим образом проиллюстрировать геометрически: на оси 0Yвозьмем–окрестность точкиА– интервали будем рассматривать все значенияxиз окрестности точки, для которых соответствующие значения функцииf(x) не выходят из- окрестности точкиА(рис. 3).

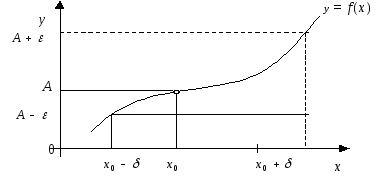
Рис. 3

Пример 1.Докажем, что функцияf(x) = 2x+ 1 приимеет предел, равный 3.

Для доказательства убедимся в том, что для любого числа можно найти такое число, что для всех значенийх, принадлежащих-окрестности 1, будет справедливо неравенство

.

Последнее неравенство можно записать так: или, что то же,. Теперь видно, что если взять, то значения функции y = 2x+1 будут отличаться от 3 по абсолютной величине меньше чем на для всех, а это и значит, что.

Следует обратить внимание на то, что в определении предела не требуется, чтобы функция f(x) была задана и в “предельной” точке, нужно только, чтобыf(x) была определена для всехxв какой-нибудь окрестности точки, исключая, быть может, саму точку.

Так, например, функция не определена в точке=2, но имеет предел как при стремлении к этой точке слева, при, так и справа. Эти пределы функции называют соответственно левым и правым пределами функции и обозначают так:и. В нашем примере эти пределы равны:

Итак, приведенная функция имеет конечные пределы справа и слева при стремлении к точке , эти пределы равны, но в самой точке функция не определена (рис. 4).

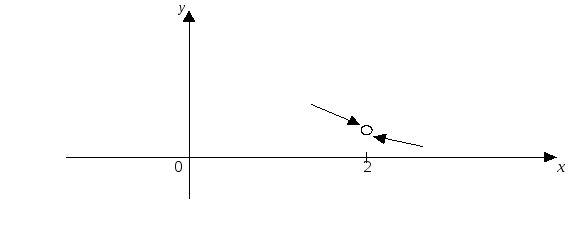
Рис. 4

1.4. Предел функции при стремлении аргумента к бесконечности (X →∞)

Пусть функция f(x) определена на всей числовой оси. ЧислоАназываетсяпределомфункции f(x) прих→∞, если для любогонайдется такое числоМ> 0, что для всехвыполняется неравенство.

Записывают это так: или.

Геометрически это означает, что для всех точек х, лежащих вне достаточно большого интервала (–M, M), значения функцииу=f(x) содержатся в как угодно малой-окрестноститочки у = А (рис.5), т.е. график функции у = f(x) для всех находится в-полосе прямой у = А,при этом он не выходит за пределы полосы.

Прямая у=Аявляется горизонтальной асимптотой кривойу=f(x).

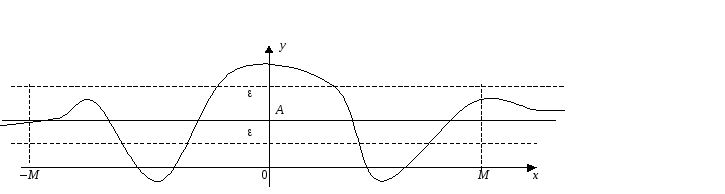
Рис. 5

Не всякая функция имеет предел на бесконечности. Если функция неограниченно возрастает на бесконечности, то она, естественно, не имеет предела на бесконечности. Даже если функция ограничена, она может не иметь предела на бесконечности. Например, функция у= sinxприизменяется от –1 до 1 и ни к какому пределу не приближается.

1.5. Бесконечно малые функции

Особое значение имеют случаи, когда при некотором изменении аргумента функция стремится к нулю.

Определение.Функцияу=f(x) называетсябесконечно малой при (может быть число или один из символов), если.

Пример1.Функцияу=x– 5 бесконечно малая при , так как.

Пример 2.Функциябесконечно малая при , так как.

Пример 3.Функцияу= sinxбесконечно малая при , так как.

Нельзя смешивать очень малое число с бесконечно малой величиной! Каждое число, как бы мало оно ни было, конечно!

Нуль есть единственное число, которое рассматривается в качестве бесконечно малой величины.