3.3. Интеграл и задача об определении площади

Заканчивая главу о первообразной, покажем, как понятие первообразной (неопределенного интеграла) теснейшим образом связано с определением площади плоской фигуры. Причем воспользуемся здесь интуитивным представлением о площади плоской фигуры, отложив точную постановку этого вопроса.

Пусть имеем непрерывную на отрезке [a,b] функциюf(x), принимающую лишь положительные (неотрицательные) значения.

Рассмотрим фигуру ABCD(рис. 24), ограниченную кривойy =f(x), прямымиx = a,x =bи отрезком оси0X; такую фигуру называют криволинейной трапецией. Изучим вопрос о площади криволинейной трапеции. Для этого возьмем некоторую переменную точкуx, лежащую на интервале [a,b], и рассмотрим площадь фигурыABLK. При измененииxэта последняя площадь будет, очевидно, соответственно изменяться, причем каждому значению переменнойxотвечает вполне определенное значение площади криволинейной трапеции. Поэтому площадь криволинейной трапецииABLKявляется некоторой функцией отx; обозначим эту функциюS(x). Найдем (если это возможно) производную функцииS(x) при измененииx. Для этого дадимxприращение (например, положительное); тогда площадьS(x) получит приращение. ОбозначимmиMсоответственно наименьшее и наибольшее значенияf(x) на промежуткеи сравним площадьс площадями прямоугольникови. Очевидно,или.

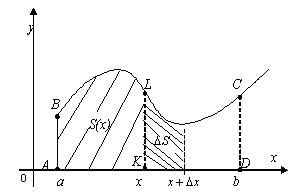
Рис. 24

Если теперь , то, вследствие непрерывностиf(x) значения,; существует предел. Таким образом, мы получили замечательный результат.

Теорема.Производная от переменной площади по переменной абсциссеxравна значению функции в этой переменной точкеf(x).

Иными словами, переменная площадь S(x) представляет собой одну из первообразных – для данной функцииy =f(x):.

Так как все первообразные отличаются друг от друга на постоянную величину c, то еслиF(x) какая-либо первообразная дляf(x), тогдаS(x) =F(x) +c.

Положив здесь x=aи считая (очевидно)S(a)=0, получим 0 =F(a) +c,c= –F(a).

Окончательно, S(x)=F(x)–F(a), гдеx– любая точка из интервала [a,b]. В частности, для получения площади всей криволинейной трапецииABCDследует взятьx=b:

.

Этот важный результат называют теоремой Ньютона-Лейбница. Мы еще встретимся с этой теоремой в дальнейшем: площадь криволинейной трапеции Sравна разности значений (произвольной) первообразнойF(x) в концах интервала [a,b].

3.4. Определенный интеграл

Вернемся вновь к задаче определения площади криволинейной трапеции, ограниченной непрерывной кривой y=f(x),, прямымиx=a,x=bи отрезком осиOX.

Разобьем отрезок [a,b] точкаминаnравных частей (рис. 25). Получимn“малых” отрезков; длина каждого отрезкаобозначается, k=1, 2, …,n; в нашем случае длины всех отрезков одинаковы:.

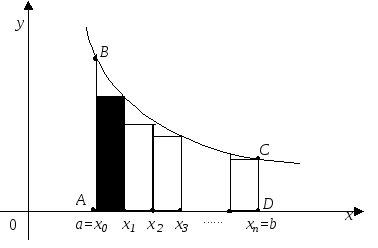
Рис. 25

Проведя через точки деления прямые, параллельные оси 0Y, мы разобьем криволинейную трапециюABCDнаnмалых криволинейных трапеций – полосок с площадью(k=1, 2,…,n). Очевидно, площадь всей криволинейной трапецииABCD

.

Эту последнюю сумму записывают так: , где греческая буква ∑ – это знак суммы, а символозначает, что суммируютсяnслагаемых при изменении индексаkот 1 доn.

Заменим теперь площадь малой криволинейной фигурыMLPQ(рис. 26) площадью прямоугольникаMLPQ, равной. Искомая площадьSкриволинейной трапеции приближенно равна площади ступенчатой фигуры:

.

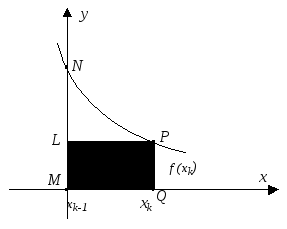
Рис. 26

Очевидно, чем меньше длина промежутков ,тем точнее ступенчатая фигура приближает нашу криволинейную трапецию.

Будем теперь увеличивать вдвое число n точек деления, уменьшая вдвое длину интервалов разбиения.

Получим последовательность сумм

, (*)

где – площадь ступенчатой фигуры изnпрямоугольников. Естественно за точное значение площадиSкриволинейной трапеции принять предел последовательностиплощадей ступенчатых фигур, когда(при этом все длиныстремятся к нулю,).

Сумма вида (*)называется интегральной суммой, а предел, к которому стремится последовательность интегральных суммпри, если такой предел существует, называется определенным интегралом функцииf(x) на отрезке [a,b] и обозначается символом(читается – интеграл отaдоbфункцииf(x)).

Итак,

.

Замечание.Мы рассмотрели здесь только частный случай последовательности интегральных сумм: разбиение отрезка [a,b] сделано так, что все(k=1, 2,…,n) равны между собой,, точкиявляются правыми концами промежутка, а функцияf(x) – непрерывна и неотрицательна. Вообще говоря, рассматриваются интегральные суммы более общего вида, а именно:

1) точки деления выбираются произвольно, не обязательно на равном расстоянии друг от друга;

2) на каждом отрезке длинывыбирается произвольная точка;

3) сумму называют интегральной суммой (Римана) для функцииf(x) на отрезке [a, b];

4) определенным интеграломназывается такое числоI, которое удовлетворяет условию: для любого (сколь угодно малого) положительного числанайдется такое положительное числоδ, что прии любом выборе точеквыполняется неравенство

.

Фактически определенный интеграл Iявляется пределом интегральных сумм при стремлении к нулю всех отрезков разбиения, если этот предел существует и не зависит от выбора точек деленияи выбора точек.

Функции f(x), для которых определенный интегралсуществует, называются интегрируемыми (по Риману) на отрезке [a,b]. К таким функциям относятся любые непрерывные на [a,b] функции, а также кусочно-непрерывные, т.е. имеющие на отрезке интегрирования лишь конечное число точек разрыва первого рода. Очевидно, что интегрируемые на отрезке функции ограничены на этом отрезке.

Возвращаясь к задаче о площади, с которой мы начали, видим, что площадь криволинейной трапеции, ограниченной непрерывной кривой y=f(x), гдена [a,b], численно равна определенному интегралу.

Этот факт выражает геометрический смысл определенного интеграла.