1. Введение в математический анализ

1.1. Числовые последовательности

С понятием предела вы уже встречались ранее в школьном курсе математики при изучении геометрической прогрессии, длины окружности, площади круга. Мы рассмотрим это понятие заново, так как оно является фундаментальным в математическом анализе.

Рассмотрим функцию, у которой областью изменения аргумента является множество всех натуральных чисел 1, 2, 3,… . Такая функция называется функцией целочисленного (натурального) аргумента а=а(n). Значения функции, соответствующие значениямn= 1,n= 2,n= 3,…, обычно обозначают символамиа₁,а₂,а₃,…,а_n,… и называют последовательностью. Значенияа₁,а₂,а₃,… называются членами последовательности, а формула, выражающаяn-й член последовательности, –формулойобщегочлена.

Рассмотрим некоторые примеры последовательностей, заданных формулой общего члена:

1) или, что то же, –1, 1, –1,…;

2) или,…;

3)

4) полагая (n = 1, 2,…), т.е. каждый член последовательности, начиная с третьего, равен сумме двух предшествующих ему членов, получим последовательность Фибоначчи: 0, 1, 1, 2, 3, 5,…

Геометрическое изображение последовательности можно получить, если построить на числовой оси точки с абсциссами, равными величинам соответствующих членов последова-тельности .

На рис. 1 изображены последовательности (а) и(б).

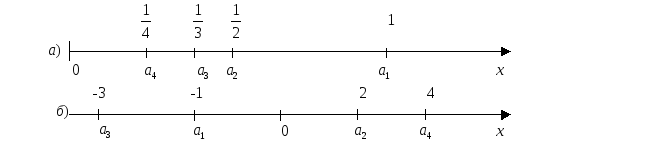
Рис. 1

Введем некоторые определения.

Последовательность называется ограниченной, если существует такое числоМ> 0, что для всехnверно неравенство.

Геометрически это означает, что все члены последовательности принадлежат интервалу (–М, М).

Последовательность, не являющаяся ограниченной, называется неограниченной.

Так, из приведенных ранее примеров последовательность ограниченная, так как; последовательность– ограниченная, так как, а последовательностиинеограниченные, так как при достаточно большихnмодули членов этих последовательностей будут больше любого наперед заданного числа.

1.2. Предел последовательности

Число aназываетсяпределомпоследовательности, если для любого, сколь угодно малого положительного числанайдется такой номерN, что для всехn > Nвыполняется неравенство.

Из этого определения следует, что для всех номеров n>N(т.е. дляn = N + 1, N + 2,…) верно неравенство.

Теперь можно сформулировать геометрически определение предела последовательности следующим образом: число aявляется пределом последовательности, если для любой–окрестности точкиа, начиная с некоторого номера, все точки попадут в эту окрестность, т.е. вне интервалаостанется лишь конечное число членов последовательности (рис. 2).

Рис. 2

Приведем несколько примеров.

Пример 1.Рассмотрим последовательность. Общий член можно переписать так:. Интуитивно понятно, что эта последовательность имеет предел, равный 1. Действительно,. Для того чтобыбыло меньше заданного положительного числа, необходимо только выполнение неравенства, которое следует из. Таким образом, по заданномувсегда можно указатьтакое , здесь [N] означает ближайшее целое число, не превосходящее , например [1,98] = 1. Так, если= 0,06, тогдаи для всех номеровn>Nбудет выполнено неравенство, т.е. число 1 есть предел последовательности. Этот факт можно записать так:.

Пример 2.Последовательность, или…, имеет предел, равный числуa= 0. Докажем это. Действительно,. Из предыдущего примера следует, чтодля всех номеров, т.е. в качестве номера N, за которым следуют номера членов последовательности, принадлежащих–окрестности нуля, можно взять номер. Так, при= 0,03 имеемN= 34, а при= 0,006 номерN=167. Итак, как бы ни было мало число> 0, существует такой номерN, зависящий от, чтодля всехn>N, т.е..

Пример 3.Рассмотрим теперь последовательность с общим членом. Члены последовательности принимают значения, равные –1 либо +1, последовательность не имеет предела. Возникает естественный вопрос: как узнать – существует ли предел данной последовательности?

Чтобы ответить на этот вопрос, введем некоторые определения.

Последовательность называется:

• возрастающей, если;

• неубывающей, если;

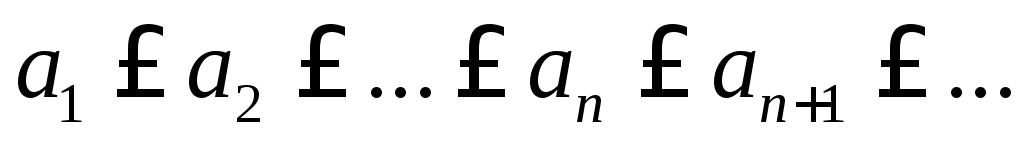• убывающей, если;

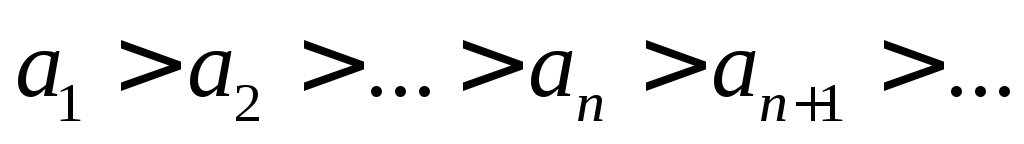• невозрастающей, если.

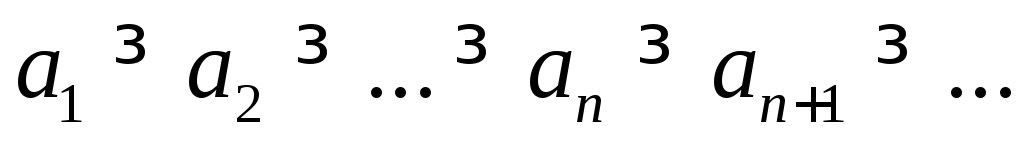Все такие последовательности называются монотонными.

Теперь сформулируем критерий существования предела последовательности.

Теорема.Монотонная ограниченная последовательность имеет предел (сходится).