1.11. Понятие непрерывности функции. Точки разрыва функции

Наиболее важным классом функций является класс непрерывных функций.

Определение. Функцияу=f(x) называетсянепрерывнойвточке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:или.

На рис. 6 изображена функция, непрерывная в точке , а на рис. 7 – разрывная, так как здесь для всехприращение функции Δyбудет больше величины “скачка” функции, равной величинеа.

Рис. 6

На рис. 7 видно, что при движении по графику функции к слева () значение функции приближается к числуA(не обязательно принимает это значение в точке). Говорят, что левый предел функции (или предел слева) при равенA. Записывают так:

_.

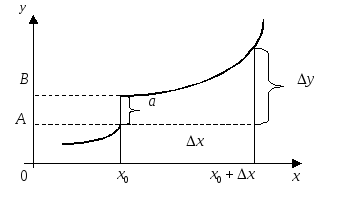
Рис. 7

Аналогично при x, стремящемся ксправа (), функция имеет предел, равный числуB:.

Иными словами, чтобы функция x=f(x) была непрерывной в точке, должны выполняться следующие условия:

1) функция определена в точке , существуетf();

2) существуют левый и правый конечные пределы функции ;

3) выполняются равенства .

Данное определение непрерывности функции в точке эквивалентно следующему.

Определение.Функцияf(x) непрерывна в точке, если.

Верны следующие теоремы.

Теорема 1.Все элементарные функции непрерывны в каждой точке своей области определения.

Теорема 2.Сумма, разность, произведение и частное непрерывных функций в данной точке есть функция, непрерывная в этой точке (для частного – знаменатель не должен обращаться в нуль в данной точке).

Теорема 3 (непрерывность сложной функции). Пустьx=f(x) непрерывна в точке, аz=g(y) непрерывна в точке, тогда сложная функцияz=g(f(x)) непрерывна в точке.

Точки разрыва.Напомним, что функцияa=f(x) непрерывна в точке, если выполнены равенства.

Если хотя бы одно из равенств не выполнено в точке , то говорят, что точкаявляется точкой разрыва функцииy=f(x) (функция терпит разрыв в этой точке).

На рис. 8 и 9 функция f(x) имеет конечные пределы справаи слева. Эти пределы равны, но значение функции в точкене существует (рис. 8) или(рис. 9). Говорят, что в точкефункцияy=f(x) имеет устранимый разрыв первого рода. Переопределив функцию в точке(рис.9), полагая, получим непрерывную в точкефункцию. Аналогично, доопределив в точкефункцию, представленную на рис. 8, полагая, вновь получим непрерывную в точкефункцию.

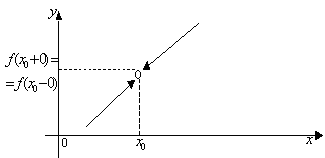
Рис. 8

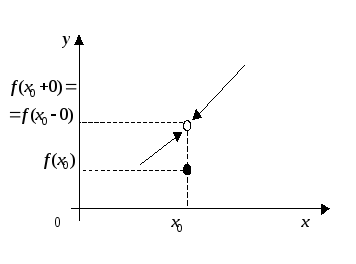
Рис. 9

Неустранимый разрыв первого рода изображен на рис. 10. Здесь , хотя оба предела существуют и конечны. Функция в точкеимеет конечный “скачок”.

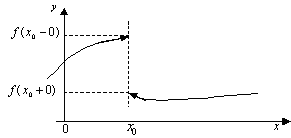
Рис. 10

Наконец, – точка разрыва второго рода для функцииy=f(x), если хотя бы один из пределовилибесконечен (рис. 11, 12).

Рис. 11

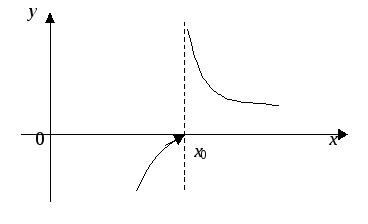
Рис. 12

Замечание.Точкаотносится к точкам разрыва второго рода также и в случае, когда хотя бы один из пределов функции справа или слева не существует. Например,в точкеx= 0 имеет разрыв второго рода.

Функции, непрерывные в каждой точке своей области определения, образуют наиболее важный класс функций. Они обладают многими замечательными свойствами. Например, для таких функций справедлива теорема Вейерштрасса: функции, непрерывные на отрезке [a,b], достигают на этом отрезке наибольшего и наименьшего значения (внутри или на границах отрезка).