2.6. Производные высших порядков

Рассмотрим дифференцируемую функцию f(x) и найдем ее производную. Эта производная является функцией переменнойx. Найдем ее производную, если она существует:.

Полученную новую функцию называют второй производной, или производной второго порядка функции f(x) и обозначают.

Продифференцировав вторую производную (если это возможно), получим производную третьего порядка: и т.д.

Определение. Производной n-го порядка функции f(x)называется первая производная от (n–1)-й производной:

Заметим, что для обозначения производных выше третьего порядка штрихи не используют, а порядок производной пишут сверху в круглых скобках: . Производные функции выше первого порядка, которую называют просто производной, называютсяпроизводными высших порядков.

2.7. Формула Тейлора (до второго порядка включительно)

Пусть функция f(x) определена в точке и ее окрестности и имеет там непрерывные производные до третьего порядка включительно. Тогда в любой точкеxиз этой окрестности функцию можно представить в виде многочлена второго порядка следующим образом:

Это представление функции называется формулой Тейлора функции f(x), а последнее слагаемоеназывают остаточным членом. При малыхявляется бесконечно малой более высокого порядка, чем.

Известные нам элементарные функции представляются многочленами от xв окрестности точки:

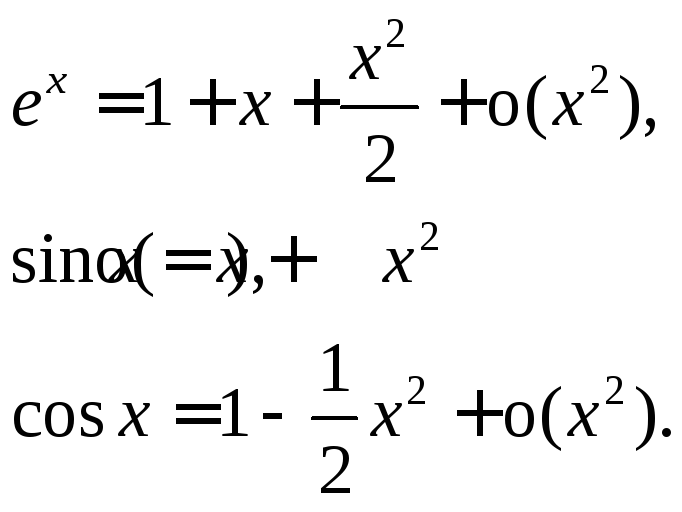
Формула Тейлора при носит название формулы Маклорена.

2.8. Выпуклость функции. Точки перегиба

Пусть функция f(x) дифференцируема на интервале [a,b].

Определение.Функцияf(x)выпукла на интервале [a, b], если касательная к графику в каждой точке, лежит не выше графика функции (под графиком):.

На рис. 19 изображена функция, выпуклая на [a,b]. Заметим, что для выпуклой функции справедливо утверждение: график функции на интервале [a,b] лежит под хордойAB. Характер выпуклости дважды дифференцируемой функции определяется знаком ее второй производной.

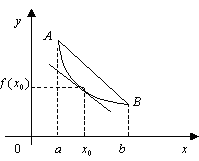
Рис. 19 Рис. 20

Справедливо следующее утверждение: пусть f(x) имеет вторую производнуюво всех точках интервала [a,b] идля всех, тогда функцияf(x) выпукла на [a,b].

В противном случае, если для всех, тоf(x) не является выпуклой на [a,b] и говорят, что она вогнута на этом интервале (рис. 20).

Определение.Точканазываетсяточкой перегиба, если точкаотделяет выпуклую часть графика от вогнутой. Очевидно, что в точке перегиба. Это условие являетсянеобходимым условием точки перегиба.

Достаточное условие точки перегиба.Если в точкеи вторая производная слева и справа от этой точки имеет разные знаки, то– точка перегиба функции.

2.9. Асимптоты

Определение.ПрямаяLназываетсяасимптотойк кривой, если расстояниеdот точкиМна кривой до данной прямойLстремится к нулю при неограниченном удалении точкиМот начала координат.

Асимптоты бывают двух типов: вертикальные и наклонные.

Прямая x=aявляется вертикальной асимптотой к графику функцииy=f(x), если точкаaесть точка бесконечного разрыва функции, т.е.(рис. 21). (Например, если знаменатель обращается в нуль приx =a, числитель же не равен нулю приx=a).

Рис. 21 Рис. 22

Прямая y = kx+b является наклонной асимптотой к графику функции y = f(x), если существуютконечные пределыи(рис. 22).

Частным случаем наклонной асимптоты является горизонтальная асимптота y=b, еслиk= 0. Заметим, что при отыскании наклонных асимптот следует отдельно рассматривать случаи.