2.4. Основные правила дифференцирования функций

Если функции идифференцируемы в точкех, то справедливы следующие правила дифференцирования:

1) , гдеc– постоянная;

2) ;

3) ;

4) ;

5) пусть функция y=f(u) дифференцируема в точкеu, а функцияu=u(x) – дифференцируема в точкеx. Тогда сложная функцияf(u(x)) дифференцируема в точкеxи ее производная вычисляется по правилуили.

Основные формулы дифференцирования

1. , гдеc– постоянная;

2. , в частности,;

3. ;

4. ,;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

Пример 1.

;

.

.

Пример 2. .

;

.

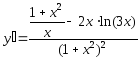Пример 3.;

;

.

2.5. Монотонные функции. Точки экстремума

Напомним, что функция f(x) называетсявозрастающей на некотором интервале, если для любых двух значений ее аргумента из этого интервала большему значению аргумента соответствует большее значение функции:(рис. 15).

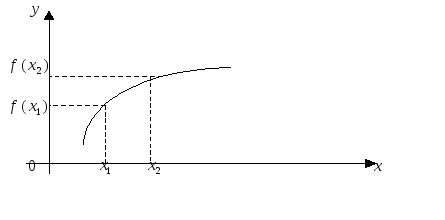
Рис. 15

Функция f(x) называется убывающейнанекотороминтервале, если большему значению аргумента соответствует меньшее значение функции:(рис. 16).

Рис. 16

Функции, возрастающие или убывающие на интервале, называются монотонными. Возрастание (убывание) функции считается нестрогим, если для.

Монотонность дифференцируемой функции определяется знаком ее первой производной.

Теорема (признак возрастания и убывания функции). Если функцияf(x) дифференцируема во всех точках некоторого интервала и производнаяположительна в каждой точке интервала, тоf(x) строго возрастает на этом интервале. Если же производнаяотрицательна во всех точках интервала, тоf(x) убывает.

Пример 1.Пусть дана функция. Необходимо исследовать поведение функции на интервале (–5, 1).

Найдем производную

.

На интервале (–5, 1) множитель (x+ 5) > 0, а (x–1) < 0, значит,и функцияy=f(x) убывает на указанном интервале.

Заметим, что утверждение, обратное сформулированному признаку, несправедливо, так как не для всякой возрастающей (убывающей) на интервале функции ее производная строго положительна (отрицательна). Например, – всюду возрастающая функция, а ее производнаяобращается в нуль приx= 0.

На рис. 17 функция возрастает на интервале , убывает на интервале, возрастает на интервале. Точкиотделяют интервалы возрастания и убывания функции. Точках₁обладает следующим свойством: значение функциибольше значений во всех “соседних” точках как слева, так и справа; в точке х₂значение функциименьше, чем значение функции во всех “соседних” точках.

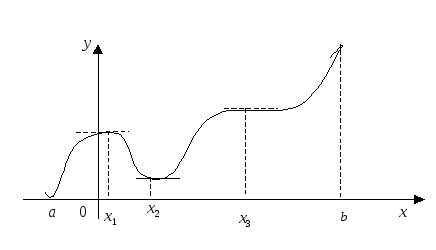
Рис. 17

Определение.Точках₁называетсяточкой максимума (max) функции f(x), если существует такая окрестностьх₁, что значениебольше любого значенияf(x) для всякогоxиз этой окрестности.

Точка х₂называетсяточкой минимума (min) функции f(x), если существует некоторая окрестностьх₂, чтоменьшеf(x) для всякогоxиз этой окрестности.

Подчеркнем локальный (местный) характер точек max и min функции. Значение функции в точке максимума (минимума) не обязано быть самым большим (малым) значением функции в ее области определения. Так, на рис. 17 видно, что значение не является наибольшим на отрезке [a,b], а– наименьшим.

Наибольшее значение функции на всей области определения называют глобальныммаксимумомфункции. Аналогично определяется глобальный минимум функции. Точки локального максимума и минимума функции называютточкамиэкстремумафункции. Точки экстремума лежат внутри интервала определения функции, а наибольшее и наименьшее значения непрерывной функции могут достигаться на концах интервала. На рис. 17 видно, что касательные, проведенные к графику функции в точкахх₁их₂(в точках экстремума), параллельны оси0X, т.е.(мы здесь рассматриваем функцию, дифференцируемую на [a, b]).

Теорема (необходимый признак экстремума).Если функцияf(x) в точке х₀имеет экстремум и дифференцируема в этой точке, то ее производная в этой точке равна нулю:.

Не следует думать, что справедливо обратное утверждение. Так, на рис. 17 , хотя очевидно, что в точке х₃нет ни min, ни max функции, хотя касательная в этой точке также параллельна оси0X.

Определение.Точки, в которых производная дифференцируемой функции равна нулю, называютсястационарными точками.

На рис. 17 точки – стационарные точки.

Как выделить среди стационарных точек точки экстремума? На рис. 17 в точках экстремума меняется характер монотонности функции, в точкех₃при движении по оси0Xслева направо характер монотонности не меняется (функция возрастает).

Теорема (достаточный признак экстремума).Если при переходе через стационарную точкуслева направо по оси0Xпроизводная функция меняет знак с (+)на (–), тох₀– точка max, если же с (–) на (+), тох₀– точка min.

Так, на рис. 17 справа от точки х₁функция возрастает, т.е., а слева отх₁функцияf(x) убывает, т.е., значит,х₁– точка максимума. Соответственно, по сформулированному признаку, точках₂– точка минимума функции.

Алгоритм отыскания точек локального min и max функции изложим на примере.

Пример 2.Найти точки экстремума функции.

1⁰. Функция определена и дифференцируема на всей числовой оси (нашли область определения и дифференцируемости функции).

2⁰. Найти стационарные точки функции, т.е. точки, в которых

,

.

–стационарные точки функции.

3⁰. Определить интервалы монотонности функции и точки max и min.

_{На числовой оси отметим стационарные точки и определим знаки производной на полученных интервалах и . Таким образом, на интервале функция возрастает , на интервале (–5,1) – убывает , в точке x = –5 производная меняет знак с (+) на (–), значит, x= –5 – точка max. В точке x = 1 производная слева , справа , значит, точка x = 1 – точка min.}

4⁰. Вычислитьи выписать ответ.

;

.

На рис. 18 в точках функция не дифференцируема (нет касательной), хотя в этих “критических точках” меняется характер монотонности функции. Можно использовать сформулированный ранее признак эктремумов функции, и в этом случае точках₁– точка max,х₂– точка min.

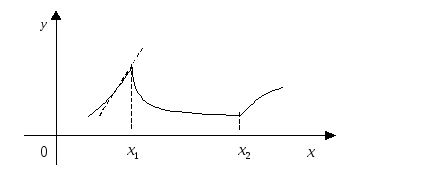
Рис. 18

На практике часто встречается задача отыскания наибольшего и наименьшего значений функции, непрерывной на замкнутом отрезке.

Алгоритм решения этой задачи рассмотрим на примере.

Пример 3.Найти наибольшее и наименьшее значения функциина отрезке [ – 6, 5].

1⁰. Находим точки, в которых производная равна нулю либо не существует. Среди найденных точек выберем те, которые находятся на отрезке.

.

.

Обе точки лежат в заданном отрезке.

2⁰. Вычислить значения функции в найденных точках и на концах отрезка.

.

3⁰. Из вычисленных значений выбрать наибольшее и наименьшее. Выписать ответ.

Ответ: наибольшее значение функция достигает на конце интервала в точке x= – 6,= 30.

Наименьшее значение достигается в точке min при x=1,.

Итак, точка x= –6 является точкой глобального максимума, а точкаx= 1 – точкой глобального минимума функции на отрезке [–6, 5].