4. Обыкновенные дифференциальные уравнения

4.1. Общие понятия и определения

Математические модели многих природных процессов и явлений можно достаточно точно описать с помощью дифференциальных уравнений.

Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимую переменнуюx, искомую функциюy=f(x) и ее производные:

.

Определение. Порядком дифференциального уравненияназывается высший из порядков производных, входящих в это уравнение.

Так, – уравнение первого порядка,– уравнение второго порядка, а– уравнение четвертого порядка.

Определение.Решением дифференциального уравненияназывается функция, которая при подстановке ее в уравнение обращает уравнение в верное равенство (тождество).

Рассмотрим пример: .

Решение этого уравнения легко угадывается. Функция y= cosxпри подстановке ее вуравнение обращает его в тождество: . Очевидно, что функцияy =sin x также является решением этого уравнения. Легко проверить подстановкой в уравнение, что

, (*),

где – произвольные постоянные, является решением при любыхи. Следует отметить, что всякое решение нашего уравнения можно получить из формулы (*) при соответствующем выбореи. Решение, записанное в виде (*), является общим решением уравнения, аy= cosx, полученная из формулы (*), при,– частное решение.

График кривой y=y(x), являющейся частным решением дифференциального уравнения, называетсяинтегральной кривой.

Точное определение общего решения дифференциального уравнения и некоторые другие поня-тия, связанные с дифференциальными уравнениями, рассмотрим для уравнений первого порядка.

4.2. Дифференциальные уравнения первого порядка. Задача Коши

Теорема существования и единственности.Уравнение вида

называется дифференциальным уравнением первого порядка.

Часто это уравнение записывается в виде , разрешенном относительно. Так, уравнениеесть уравнение первого порядка, здесь. Функция, гдеc– произвольная постоянная, удовлетворяет уравнению, т.е. является его решением.

Гиперболы, полученные при конкретных c, являются интегральными кривыми, а совокупность всех интегральных кривых образует однопараметрическое семейство интегральных кривых (рис. 34). Константа cявляется параметром.

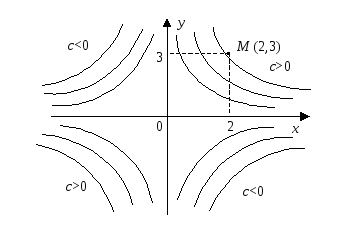
Рис. 34

Из семейства интегральных кривых можно выбрать конкретную кривую (частное решение), проходящую через точку ,. В общее решениеподставим координаты точкиMи найдем соответствующее значение,с=6. Кривая– искомое решение. Рассмотренная задача является задачей Коши.

Задача Коши для уравнения. Найти решениеy =y(x) уравнения, удовлетворяющее начальным условиямили.

Встает вопрос: всегда ли существует решение задачи Коши? Ответ на этот вопрос дает следующая теорема.

Теорема(существования и единственности). Если правая часть уравнения– функцияf(x,y) и ее частная производнаяопределены и непрерывны в некоторой областиDизменения переменныхx,y, то какова бы ни была внутренняя точкаэтой области, данное уравнение имеет единственное решениеy=y(x), причем при,.

В рассмотренном ранее примере , правая частьудовлетворяет условиям теоремы всюду, кроме прямойx=0, областьD– вся плоскость, кромеx= 0. Точка=(2, 3) принадлежит областиD, через эту точку проходит единственная интегральная кривая уравнения.

Общим решением уравненияявляется функцияy =y(x,c), зависящая от аргументаxи произвольной постояннойс, удовлетворяющая условиям:

1) при любых значениях постоянной cфункцияy =y(x,c) является решением уравнения;

2) для любой точки , лежащей внутри областиD, существует единственное значение постояннойтакое, что.

Частным решением уравнения является решение, полученное из общегоy = y(x, c),при конкретном значении.

Общее решение дифференциального уравнения, найденное в виде (не разрешенном относительноy), называютобщиминтеграломуравнения.