3.5. Вычисление определенного интеграла. Основные свойства

Впервые со словом “интеграл” и символом мы встретились, когда вводили понятие первообразнойF(x) для функции f(x)и неопределенного интеграла. Решая в предыдущем параграфе задачу о площади криволинейной трапеции, мы получили определенный интеграл . (Символ ∫происходит от вытянутой латинской буквыS, начальной в слове summa). Безусловно, это не случайно. Оказывается, с помощью неопределенного интеграла (первообразной) получен способ вычисления определенного интеграла. Для вычисления определенного интеграла применяетсяформула Ньютона-Лейбница:

,

где F(x) – одна из первообразныхf(x), и определенный интегралравен разности значения первообразнойF(x) в верхнем пределе интегрированияF(b) минус значениеF(x) в нижнем пределе интегрированияF(a).

Вспомним, что при вычислении площади криволинейной трапеции в пп. 3.3 мы уже встречались с этой формулой.

Разность F(b)–F(a) символически обозначают.

Пример 1.Вычислить.

Вычислим сначала первообразную от , затем по формуле Ньютона-Лейбница:

.

Пример 2.Вычислить площадьS, ограниченную кривойи осью0X.

Начертим график параболы и рассмотрим искомую площадьS(на рис. 27 площадьSзаштрихована).

Рис. 27

Было показано, что площадь криволинейной трапеции, ограниченной непрерывной функцией f(x),на интервале [a,b], вычисляется как. В нашем случае на отрезке [0, 2] функция, и искомая площадь может быть вычислена по формуле, так какна отрезке [0, 2].

Итак, .

Основные свойства определенного интеграла:

1. .

2. .

3. c – постоянная.

4. Если интервал интегрирования [a,b] разбит точкойcна части [a,b] и [c,b], то.

Геометрически выполнение свойства 4 очевидно (рис. 28).

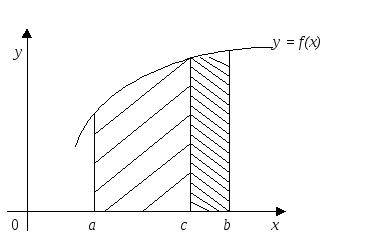
Рис. 28

5. Если функция на интервале [a,b], то. Еслии, то.

6. Если для всех выполняется условие, то.

Геометрический смысл свойства 6 определенного интеграла показан на рис. 29.

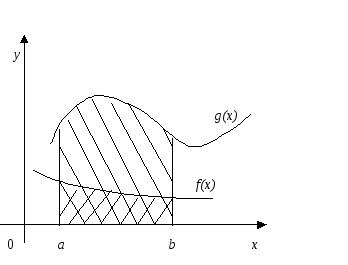
Рис. 29

Доказательство всех свойств 1 – 6 очевидно следует из определения определенного интеграла.

7.Теорема о среднем значении определенного интеграла.

Если f(x) напрерывна на [a,b], то существует такая точка ξ внутри интервала, что.

Геометрически последнее утверждение означает: существует такая точка ξ на интервале [a,b], что площадь криволинейной трапеции, ограниченной непрерывной кривойy=f(x), равна площади прямоугольника с основанием (b–a) и высотой(рис. 30).

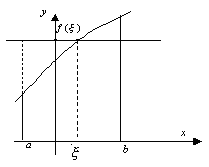
Рис. 30

8.Теорема об оценке интеграла.

Если f(x) непрерывна на отрезке [a,b], аm– наименьшее,M– наибольшее значения функции на [a,b], тои(рис. 31).

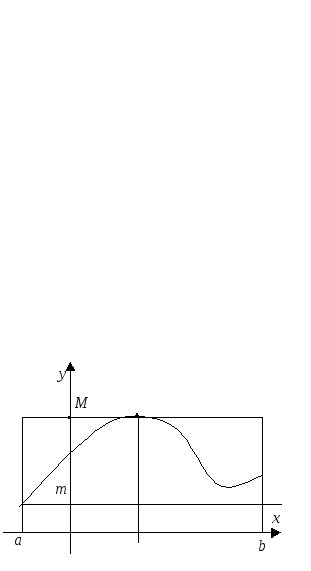
Рис. 31

Рассмотрим еще несколько примеров.

Пример 3.Вычислить.

Вычислим этот интеграл, сделав подстановку u= lnx,. Функция lnxи ее производная непрерывны на интервале (1, 2). При замене переменной в определенном интеграле отпадает необходимость возвращения к первоначальной переменной, но в интеграле следует поменять пределы интегрирования.

Положим x= 1, тогдаu= lnx = ln1 = 0; еслиx = 2, тоu= lnx = ln2, и новые пределы интегрирования по переменнойuбудут отu = 0 доu= ln 2:

.

Пример 4. Вычислить . Заметим, что подынтегральная функцияy =sin x нечетная, а область интегрирования – отрезок, симметричный относительно начала координат. Из геометрических соображений такой интеграл будет равен нулю (рис. 32).

Рис. 32

Действительно,

.

Интеграл от нечетной функции на симметричном относительно начала координат отрезке равен нулю.

Если же функция y=f(x) четная (рис. 33), то.

Рис. 33

Пример 5.

или .

Интеграл от четной функции на симметричном относительно начала координат отрезке [–a,a] равен удвоенному интегралу по отрезку [0,a].

Рассмотрим, как применяется формула интегрирования по частям в определенном интеграле:

Пример 6.Вычислить.

Пусть u=x,. Тогда.

.

Мы ознакомились в этой главе только с основными понятиями интегрального исчисления. Многие методы вычисления первообразной, несобственные интегралы, приложения определенного интеграла, вопросы приближенного вычисления и др. не входят в круг рассмотрения этого пособия.