4.3. Способы интегрирования уравнений первого порядка

Операцию отыскания решения дифференциального уравнения называют интегрированием уравнения. Мы рассмотрим лишь два простых класса дифференциальных уравнений, для которых находится общее решение.

Уравнения с разделяющимися переменными.К таким уравнениям относятся уравнения вида, где.

Для интегрирования уравнение запишем в виде

.

Простыми преобразованиями перепишем уравнение так:

.

Переменные разделились: слева записан дифференциал некоторой функции от y, а справа – отx. Проинтегрируем обе части полученного уравнения:или– получили общее решение уравнения (возможно, в неявном виде).

Замечание.При делении уравнения наh(y) предполагается, что(могли потерять решение уравнения).

Пример 1. .

Перепишем уравнение в виде .

Функции y=0 иy= –2являются решениями уравнения. Остальные решения найдем, разделив переменные и интегрируя полученное уравнение:

.

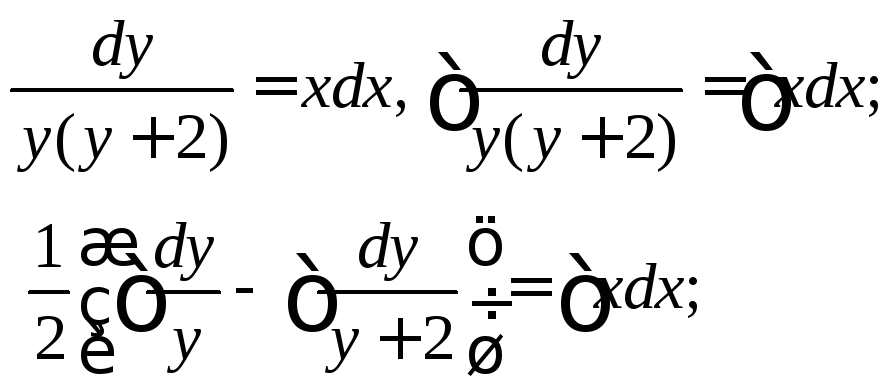
Произвольную постоянную здесь удобно записать как . Тогдаили.

Линейные дифференциальные уравнения первого порядка.

Уравнение вида , гдеp(x) иq(x) – заданные непрерывные функции, называется линейным (функцииy(x) ивходят в уравнение лишь в первой степени).

Решение этого уравнения будем искать в виде или, коротко,, тогда; подставив в уравнение, получим

.

Выберем множитель u(x) так, чтобы, тогда исходное уравнение сводится к интегрированию двух уравнений с разделяющимися переменными:

, (1)

. (2)

Найдем решение уравнения (1). Пусть u(x) – некоторое решение. Подставимu(x) во второе уравнение и найдем его общее решение. Тогда общим решением исходного уравнения будет функция.

Пример 2..

Ищем решение этого уравнения в виде . Имеем,.

Функцию uвыберем так, чтобы

(3)

Получили уравнение с разделяющимися переменными. Решим это уравнение:

или

Функция является решением этого уравнения. Функциюнаходим из уравнения, подставив найденную функциюu=x²:

. (4)

Вновь получили уравнение с разделяющимися переменными. Разделяя переменные, получим , или. Общим решением этого уравнения будет функция.

Следовательно, все решения исходного уравнения определяются формулой или.

4.4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение

,

Где – постоянные, называетсялинейным однородным дифференциальным уравнением с постоянными коэффициентами.

Решение этого уравнения будем искать в виде , тогда,. Подставив в уравнение, получим, так как, то функциябудет решением дифференциального уравнения, еслиrудовлетворяет алгебраическому уравнению

. (*)

Последнее уравнение называют характеристическим уравнением для исходного дифференциального.

Уравнение (*) имеет два корня .

Рассмотрим возможные случаи:

1) при D > 0 уравнение (*) имеет действительные различные корни . Функции– решения дифференциального уравнения, они образуют фундаментальную систему решений исходного дифференциального уравнения;

2) при D= 0 корни уравнения (*) действительные и кратные, т.е., тогда фундаментальная система решений состоит из функцийи;

3) при D<0 уравнение (*) имеет комплексно сопряженные корни, где, фундаментальная система решений состоит из функций.

Общее решение дифференциального уравнения с постоянными коэффициентами есть линейная комбинация решений фундаментальной системы, т.е. , где– произвольные постоянные.

Уравнение

называется линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами . Функцияf(x) называется правой частью уравнения. Уравнениес теми же коэффициентаминазывают однородным дифференциальным уравнением, соответствующим данному неоднородному. Общее решение неоднородного дифференциального уравненияY(x) есть сумма общего решения соответствующего однородногоy(x) и частного решения неоднородного:

.

Основная трудность состоит в нахождении . Однако существует простой способ нахождения частного решенияв том случае, когда правая частьf(x) имеет специальный вид. Способ этот заключается в подборе частного решения в зависимости от вида правой части (метод неопределенных коэффициентов).

1. Пусть правая часть уравнения имеет вид , где– заданный многочлен степениm,– действительное число.

Тогда частное решение ищем в виде, где– многочлен той же степениm, что и, но с неизвестными коэффициентами;k– кратность действительного корня α характеристического уравнения. Для отыскания коэффициентовследует подставитьв исходное уравнение, поделить обе части наи приравнять коэффициенты при одинаковых степеняхх. Получим систему линейных уравнений для определения неизвестных коэффициентов.

2. Пусть правая часть дифференциального уравнения имеет вид , где– заданные числа. Тогда частное решение следует искать в виде

,

где A,B– неизвестные постоянные,k– кратность комплексных корнейхарактеристического уравнения.

Разберем несколько примеров.

Пример 1.Найти общее решение уравнения.

Решение.Составим характеристическое уравнение; его корни(можно найти по теореме Виета), им соответствует фундаментальная система решений (ФСР)и общее решение имеет вид.

Пример 2.Найти общее решение уравнения.

Решение.Характеристическое уравнениеилиимеет кратный корень, ФСР:, общее решение.

Пример 3.Найти общее решение уравнения.

Решение.Характеристическое уравнение. Корни его найдем, используя общую формулу

.

Следовательно, . Корни характеристического уравнения комплексные, а потому им соответствуют частные решенияи, составляющие ФСР. Следовательно, общее решение есть

.

Пример 4.Найти общее решение неоднородного дифференциального уравнения с постоянными коэффициентами.

Решение.Характеристическое уравнение соответствующего однородного дифференциального уравненияимеет вид, его корнями будут числа; ФСР образуют функции, общее решение соответствующего однородного уравнения.

Частное решение исходного уравнения следует искать в виде , так как коэффициентом прислужит многочлен нулевой степени (, т.е. m=0), числоне является корнем характеристического уравнения (k= 0,k– кратность корня α = 5).

Итак, .

Подставим в данное уравнение , или, отсюда

12A= 1,и.

Общее решение исходного уравнения .

Пример 5.Найти общее решение неоднородного дифференциального уравнения.

Решение.Характеристическое уравнение соответствующего однородного уравненияимеет различные вещественные корни, а потому общее решение однородного уравнения.

Частное решение неоднородного уравнения следует искать в виде , так как правая часть уравнения,

и не является корнем характеристического уравнения,k=0.

Подставим решение в исходное уравнение (в колонке слева записаны коэффициенты прив данном уравнении):

–2
1
1

или

.

Таким образом, имеем систему

,

т.е. A= –0,3;A= –0,9.

Получили частное решение .

Следовательно, общее решение данного уравнения имеет вид

.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ