Лекція № 16 Означення та неперервність елементарних функцій.

Як приклад застосування властивостей та теорем доведених у минулих лекціях означимо елементарні функції на та доведемо їх неперервність.

1. Степенева функція.

Розглянемо функцію яка, згідно з властивостями неперервних функцій, неперервна як добутокn неперервних функцій .

Крім того, функція як композиція неперервних функційтеж є неперервною на всій множині.

Отже степенева функція з раціональним показником(якщотоіозначена вище, якщо, тоі) - коректно означена наі неперервна на всій множині.

Не складно довести, що функція строго зростаюча, астрого спадаюча.

Крім того, виконуються всі властивості степенів, доведення котрих ми залишаємо для самостійної роботи.

2. Показникова функція.

Нехай довільне число. Тоді для будь-якого, згідно з існуванням степеневої функції, існує числоі виконуються властивості:

1. Якщо , то.

Доведення. Оскільки , тодля будь-якого. Тоді для будь-якого, тобтоабодля будь-якого. Отже

.

2.

Доведення. Спочатку покажемо, що .

(за нерівністю Бернуллі). Отже приі з властивості граничних переходів в нерівностях маємо, щопри. Таким чином.

Покажемо, що . Нехайпри. Для кожногоіснуєтаке, щопри(оскільки). Тоді

.

Оскільки при(з вище доведеного) то згідно з властивостями граничних переходів в нерівностях маємо, що. Оскільки рівність доведена для будь-якої послідовності,при, то за ознакою Гейнеіснує і дорівнює 1.

Введемо означення показникової функції для .

Якщо , то (згідно з наслідками принципу Архімеда) існуєтакі, що, отже. Для будь-якихі. Таким чином множинаобмежена зверху, а множинаобмежена знизу, отже існують числа(з означень точної верхньої та нижньої границі). Покажемо, що. За означенняммаємо, де, отже. Оскільки при, маємо:таке, що якщо, то, звідки.

Означення. Для будь-якого визначимоТаким чином, для будь-якогокоректно визначена показникова функція.

Властивості показникової функції.

1. При функціястрого зростаюча. Дійсно, якщо, то існуютьі,(згідно принципу Архімеда). Отже за означеннямта попередньо доведеної властивості 1, маємо

.

2. Функція () неперервна на.

Покажемо, що значення заповнюють множину. НехайіØ.

Оскільки з нерівності , то длямаємо. З аксіоми повноти, існуєтакий, щодля. Покажемо, що.

Якщо то, оскількипри, існує, що, але з нерівності(у зв’язку з тим, щорозділяє множини А і В). Однак, за означенням множин А і В, маємоØ, це протирічить вище отриманим включенням. Отже наше припущення невірне, тобто. Аналогічно отримаємо, протиріччя, якщо припустимо, тобто.

За теоремою про монотонну функцію, яка заповнює значеннями проміжок, маємо що неперервна на.

Якщо то, деі функціявизначена і неперервна (за властивостями неперервних функцій) та спадаюча на.

3. Логарифмічна функція.

Функція обернена до функції називається логарифмічною функцією. За теоремою про обернену функцію вона існує та неперервна і монотонна (в залежності від). З властивостей степенів виконується відповідні властивості логарифмів, які ми залишаємо на самостійне вивчення.

4. Степенева функція з довільним показником.

Нехай , тоді степеневою функцією з показникомвизначимо функціюяка існує та неперервна, за теоремою про композицію неперервних функцій.

Лекція № 17

Повні простори. Зв'язок повноти і компактності. Ознака Коші. Теорема про нерухому точку.

1. Означення і ознаки повноти.

Означення. Нехай в метричному просторі Е задана послідовність . Говорять, що це послідовність Коші (фундаментальна), якщо:

(властивість метрична, а не топологічна).

Властивості.

1. Якщо послідовність {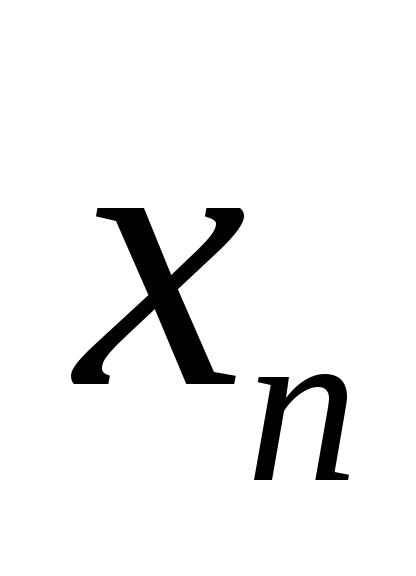} збіжна, то вона є послідовність Коші.

1. Будь-яка послідовність Коші обмежена.

2. Будь-яка підпослідовність послідовності Коші сама є послідовністю Коші.

3. Якщо послідовність Коші має граничну точку, то вона збігається до неї.

Означення. Метричний простір Е називається повним, якщо будь-яка послідовність Коші збіжна в даному просторі.

Теорема. Будь-який метричний простір Е, усі замкнуті кулі якого компактні, повний. В частинному випадку: повний, будь-який метричний, компактний простір; будь-який скінчено вимірний нормований векторний простір.

Доведення. Оскільки кожна послідовність Коші обмежена, то міститься в деякій замкнутій кулі В, тобто в деякому компакті. За теоремою Больцано-Вейєрштрасса вона має граничну точку. Отже, послідовність збігається до цієї граничної точки і простір Е повний.

Наприклад. 1. -повний за теоремою.

2. - не є повною множиною.

Будь-який метричний простір можна доповнити до повного. Тому, як правило, розглядаються тільки повні простори.